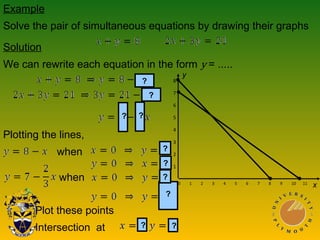
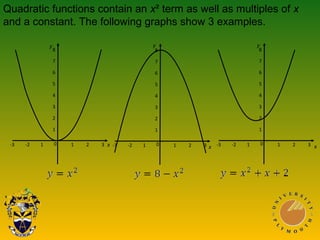
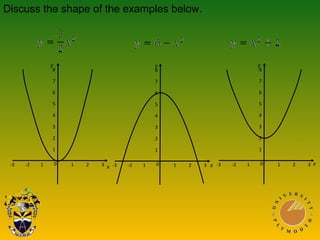
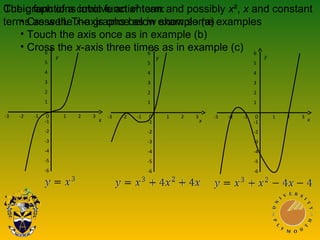
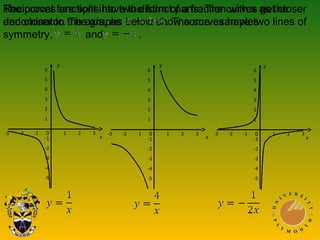
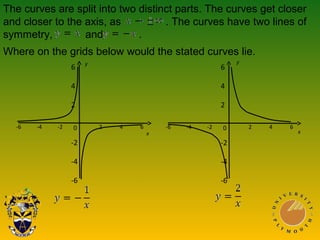
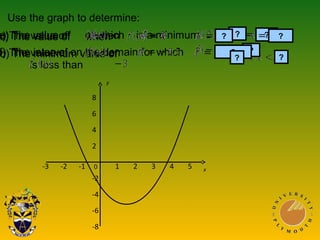
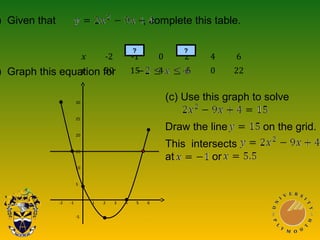
This document discusses using graphs to solve equations. It covers solving simultaneous equations by graphing the lines and finding their intersection point. It also discusses graphs of quadratic, cubic, and reciprocal functions, including their key characteristics and shapes. Examples of each type of function are shown. The document concludes by discussing using graphs to find specific values or intervals related to equations.

1. Unit 29
Using Graphs to Solve Equations
Presentation 1
Solution of Simultaneous Equations Using Their Graph
Presentation 2 Graphs of Quadratic Functions
Presentation 3 Graphs of Cubic Function
Presentation 4 Reciprocal Functions
Presentation 5 Graphical Solutions of Equations

2. Unit 29
29.1 Solution of Simultaneous
Equations Using Their Graphs

3. Example
Solve the pair of simultaneous equations by drawing their graphs
Solution
We can rewrite each equation in the form y = .....
Plotting the lines,
when
when
Plot these points
Intersection at ?
?
?
?
?
?
?
?
?
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 11
?
x
y

4. Unit 29
29.2 Graphs of Quadratic
Functions

5. Quadratic functions contain an x² term as well as multiples of x
and a constant. The following graphs show 3 examples.
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
x
y
x
y
x
y

6. Discuss the shape of the examples below.
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
8
7
6
5
4
3
2
1
-3 -2 1 1 2 30
x
y
x
y
x
y

7. Unit 29
29.3 Graphs of Cubic Function

8. Cubic functions involve an x³ term and possibly x², x and constant
terms as well. The graphs below show some examples
-3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
0 -3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
0 -3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
0
The graph of a cubic function can:
• Cross the x-axis once as in example (a)
• Touch the axis once as in example (b)
• Cross the x-axis three times as in example (c)
x
y
x
y
x
y

9. Unit 29
29.4 Reciprocal Functions

10. -3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
0 -3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
0 -3 -2 -1 1 2 3
6
5
4
3
2
1
-1
-2
-3
-4
-5
0
Reciprocal functions have the form of a fraction with x as the
denominator. The graphs below show some examples
The curves are split into two distinct parts. The curves get closer
and closer to the axis, as . The curves have two lines of
symmetry, and .
x
y
x
y
x
y

11. The curves are split into two distinct parts. The curves get closer
and closer to the axis, as . The curves have two lines of
symmetry, and .
Where on the grids below would the stated curves lie.
6
4
2
-2
-4
-6
-6 -4 -2 2 4 60
6
4
2
-2
-4
-6
-6 -4 -2 2 4 60
x
y
x
y

12. Unit 29
29.5 Graphical Solutions of
Equations

13. c) The value of when or
d) The minimum value of
e) The value of at which is a minimum
f) The interval on the domain for which
is less than
?
??
8
6
4
2
-2
-4
-6
-8
-3 -2 -1 1 2 3 4 50
Use the graph to determine:
a) The value of when
b) The value of when ??
??
?
x
y

14. x -2 -1 0 2 4 6
y 30 15 4 -6 0 22
) Given that , complete this table.
) Graph this equation for
? ?
-2 -1 1 2 3 4 5 6
30
25
20
15
10
5
-5
(c) Use this graph to solve
Draw the line on the grid.
This intersects
at or