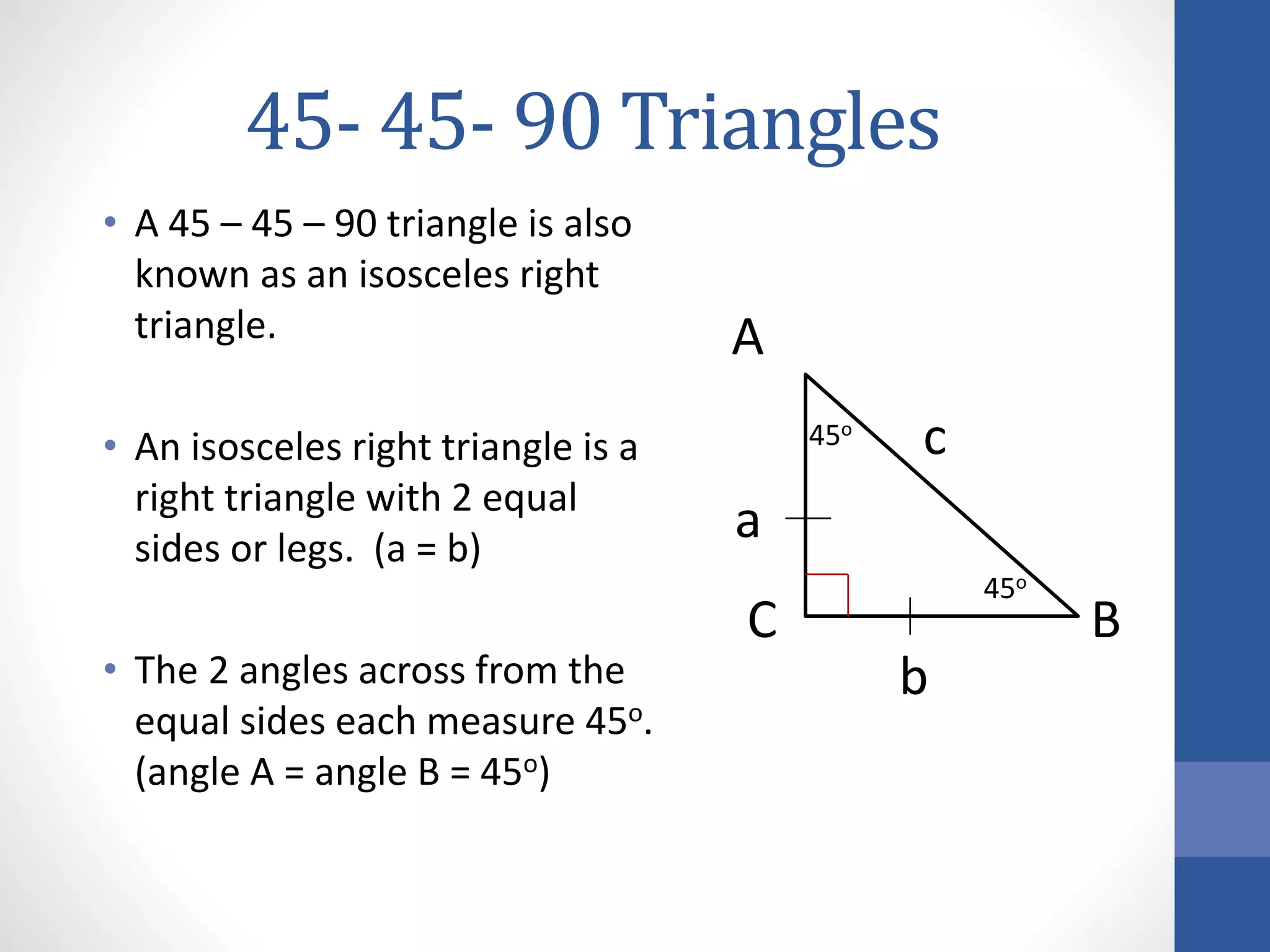
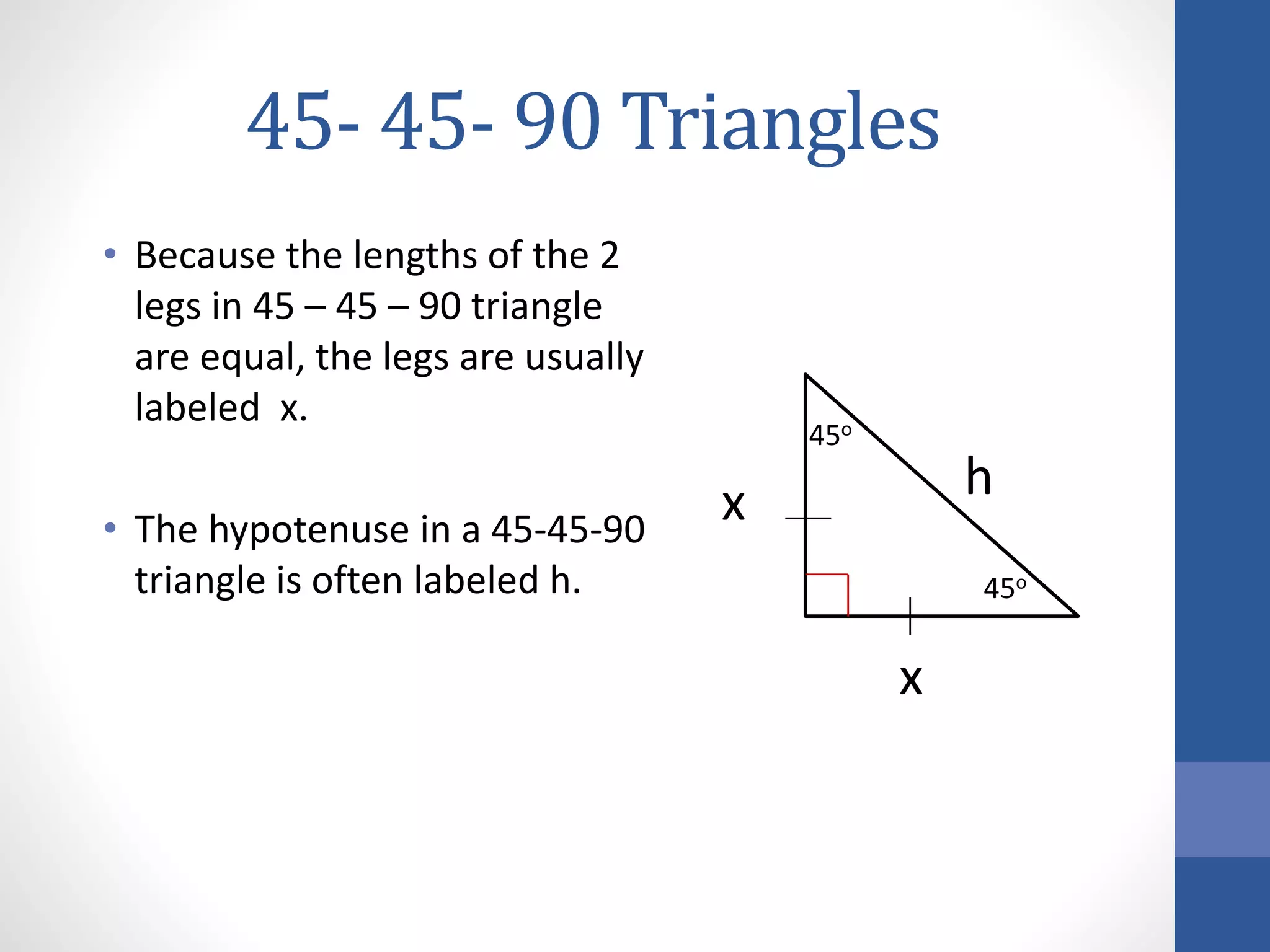
This document discusses 45-45-90 triangles, also known as isosceles right triangles. It provides properties of these triangles, including that the two legs are equal and each measure 45 degrees. Shortcuts are presented for calculating side lengths without using the Pythagorean theorem, such as that the hypotenuse h equals the leg length x squared, and that each leg x equals h squared over 2. Several practice problems demonstrate applying these shortcuts to find missing side lengths.

1. Special Right
Triangles
45 – 45 – 90 Triangles

2. Special Right Triangles
Directions
As you view this presentation, take
notes and work out the practice
problems.
When you get to the practice problem
screens, complete the step in your
notebook before continuing to the
next slide.

3. 45- 45- 90 Triangles
• A 45 – 45 – 90 triangle is also
known as an isosceles right
triangle.
• An isosceles right triangle is a
right triangle with 2 equal
sides or legs. (a = b)
• The 2 angles across from the
equal sides each measure 45o.
(angle A = angle B = 45o)
c
a
b
45o
45o
A
C B

4. 45- 45- 90 Triangles
• Because the lengths of the 2
legs in 45 – 45 – 90 triangle
are equal, the legs are usually
labeled x.
• The hypotenuse in a 45-45-90
triangle is often labeled h.
hx
x
45o
45o

5. 45- 45- 90 Triangles
Findingthe Length of the Hypotenuse
• The Pythagorean Theorem
can be used to find the length
of the hypotenuse when
given the length of the legs.
• x2 + x2 = h2
• 2x2 = h2
• 𝑥2 ∗ 2 = h2
• x 2 = h
• You can save a lot of time and
work if you remember
h = x 2
hx
x
45o
45o

6. 45- 45- 90 Triangles
Practice Problem 1
• Find the length of x
h
x = ?
5
45o
45o

7. 45- 45- 90 Triangles
Practice Problem 1
• Find the length of x
• The two legs of a 45 – 45 – 90
triangle are equal so
x = 5
h
x = 5
5
45o
45o

8. 45- 45- 90 Triangles
Practice Problem 1
• Find the length of h
h = ?
x= 5
5
45o
45o

9. 45- 45- 90 Triangles
Practice Problem 1
• Find the length of h
• You can always use the
Pythagorean Theorem to find
the length of h.
• But if you remember the
shortcut
h = x 2
x = 5
5
45o
45o

10. 45- 45- 90 Triangles
Practice Problem 1
• Find the length of h
• You can always use the
Pythagorean Theorem to find
the length of h.
• But if you remember the
shortcut
• h = 5 2
h = 5 2
x = 5
5
45o
45o

11. 45- 45- 90 Triangles
Findingthe Lengths of the Legs
• The Pythagorean Theorem can be used
to find the lengths of the legs when
given the length of the hypotenuse.
• x2 + x2 = h2
• 2x2 = h2
• x2 =
ℎ2
2
• 𝑥2 =
ℎ2
2
• x =
ℎ
2
*
2
2
=
ℎ 2
2
• (Remember to always rationalize the
denominator)
hx
x
45o
45o

12. 45- 45- 90 Triangles
Findingthe Lengths of the Legs
You can save a lot of time
and work if you remember
x =
ℎ 2
2 h
x =
ℎ 2
2
x =
ℎ 2
2
45o
45o

13. 45- 45- 90 Triangles
Practice Problem 2
• Find the length of x
h = 3
x = ?
x = ?
45o
45o

14. 45- 45- 90 Triangles
Practice Problem 2
• Find the length of x
• You can always use the
Pythagorean Theorem to find
the lengths of the legs.
h = 3
x = ?
x = ?
45o
45o

15. 45- 45- 90 Triangles
Practice Problem 2
• Find the length of x
• But if you remember the
shortcut
• x =
ℎ 2
2
h = 3
x =
ℎ 2
2
45o
45o
x =
ℎ 2
2

16. 45- 45- 90 Triangles
Practice Problem 2
• Find the length of x
• But if you remember the
shortcut
• x =
ℎ 2
2
• Then x =
3 2
2
h = 3
x =
3 2
2
45o
45o
x =
3 2
2

17. 45- 45- 90 Triangles
Practice Problem 3
• Find the length of x
h = 1
x = ?
x = ?
45o
45o

18. 45- 45- 90 Triangles
Practice Problem 3
• Find the length of x
• You can always use the
Pythagorean Theorem to find
the lengths of the legs.
h = 1
x = ?
x = ?
45o
45o

19. 45- 45- 90 Triangles
Practice Problem 3
• Find the length of x
• But if you remember the
shortcut
• x =
ℎ 2
2
h = 1
x =
ℎ 2
2
45o
45o
x =
ℎ 2
2

20. 45- 45- 90 Triangles
Practice Problem 3
• Find the length of x
• But if you remember the
shortcut
• x =
ℎ 2
2
• Then x =
1 2
2
=
2
2
h = 1
x =
2
2
45o
45o
x =
2
2

21. 45- 45- 90 Triangles
in the Unit Circle
• In the Unit Circle:
• h = 1
• So remembering this
shortcut for a 45 – 45 - 90
triangle will save you time
and work.
• x =
2
2
h = 1
x =
2
2
45o
45o
x =
2
2