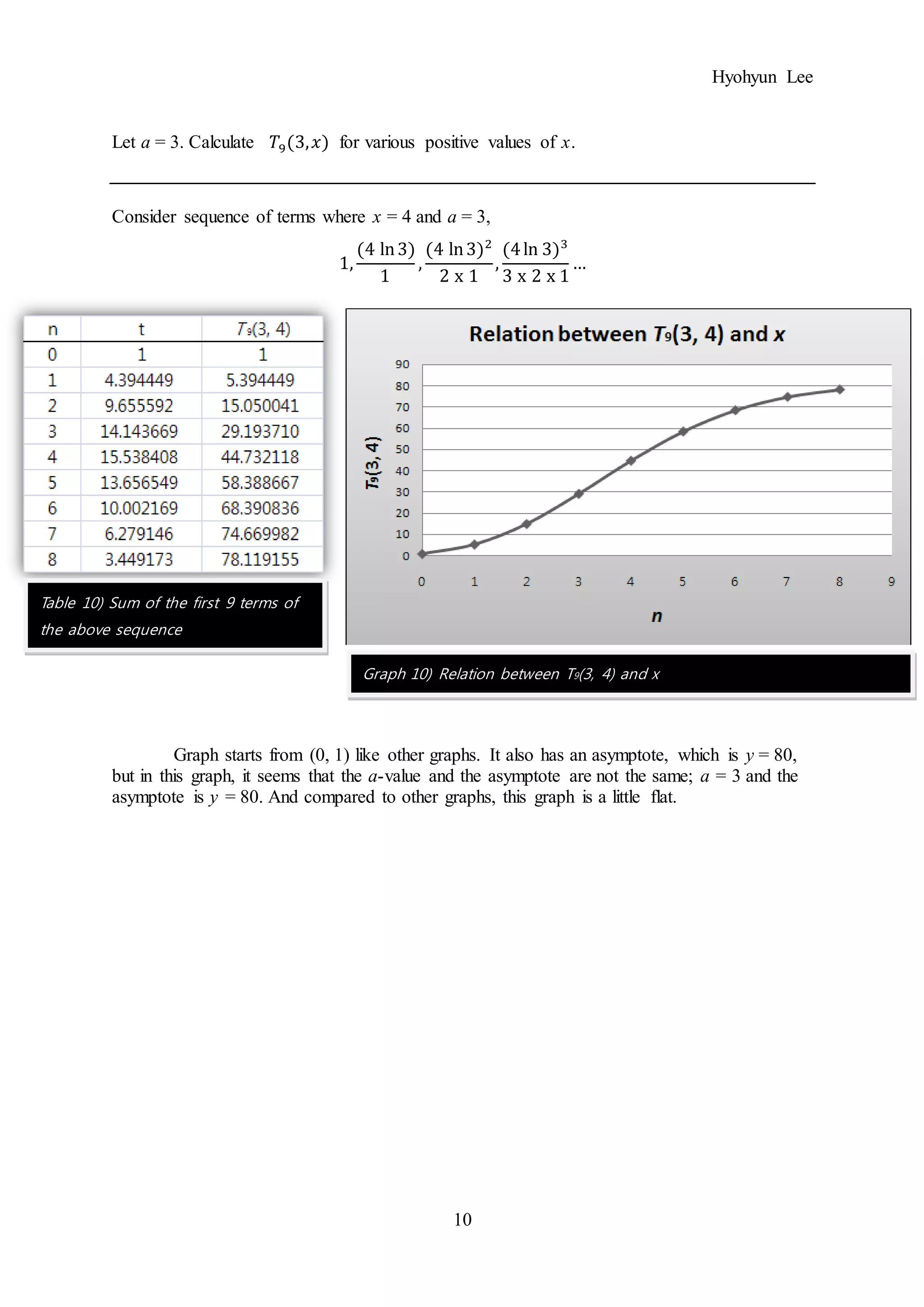
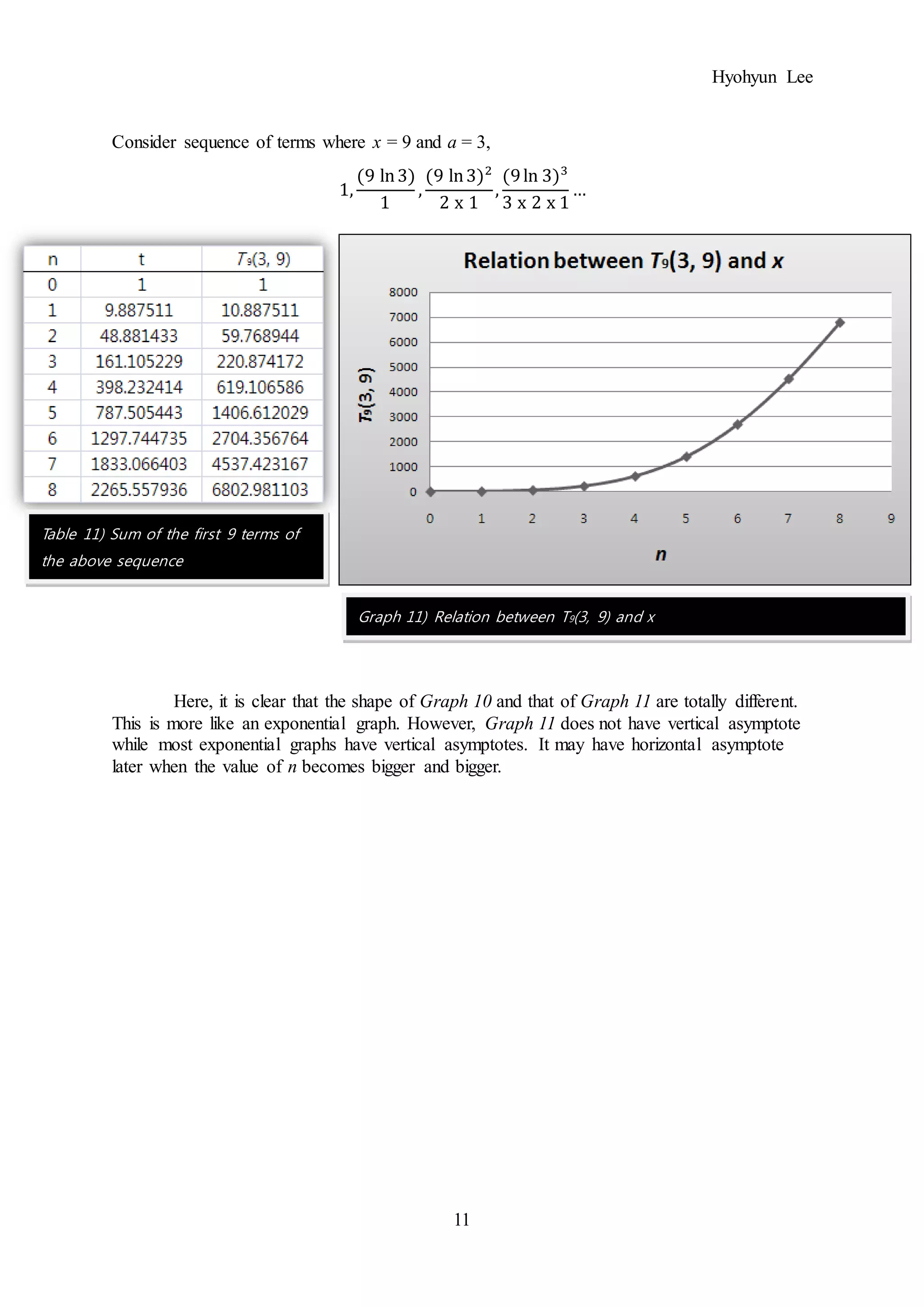
The document investigates an infinite sequence where terms are defined using natural logarithms and factorials. Six graphs are presented showing the relationship between the partial sum Sn and n for different values of variables a and x. The graphs demonstrate that as a increases, the increasing period at the beginning gets longer, and Sn approaches a as the asymptote. Further graphs show that for a fixed a, the shape of the graph becomes more exponential-like as x increases.

1. Hyohyun Lee
1
The purpose of this assignment is to investigate the sum of the infinite sequences 𝑡 𝑛, where
𝑡0 = 1, 𝑡1 =
(𝑥ln𝑎)
1
, 𝑡2 =
(𝑥ln𝑎)2
2 x 1
, 𝑡3 =
(𝑥ln𝑎)3
3 x 2 x 1
…, 𝑡n =
(𝑥ln𝑎)n
𝑛!
There used several notations and basic operations in this sequence. Firstly, function
ln is used in numerators. It can be expected that the graph of this sequence will appear as
similar as the graph of y = ln(x). In addition, as the terms go further, each term has equations
which are growing exponentially. In denominators, the factorial notation n! is used.
n! = n(n-1)(n-2)…3 x 2 x 1; 0! = 1
By using these basic notations, the purpose of this assignment will be achieved.
Consider the following sequence of terms where x = 1 and a = 2,
1,
(ln2)
1
,
(ln2)2
2 x 1
,
(ln2)3
3 x 2 x 1
…
From Graph 1, it can be seen that the shape of the plot itself is similar to that of y =
log(x) graph or y = ln(x) graph. However, while the y = ln(x) graph has two asymptotes:
vertical and horizontal, Graph 1 has only horizontal asymptote, which is y = 2. To be more
specific, in Graph 1, when x = 0, it can be seen that the x has a right y-value, which is 1. On
the contrary, in y = ln(x), when x = 0, there is no right y-value because the graph does not
touch the x = 0, which is a vertical asymptote.
Furthermore, it is obvious that when x = 1, the a-value is the same as an asymptote in
graph. Table 1 shows that the sum of the first ten terms approaches to 2 and the Graph 1 also
shows that the line does not cross or touch y = 2.
0
0.5
1
1.5
2
2.5
0 2 4 6 8 10 12
Sn
n
Relation between Sn and n
Sum
Table 1) Sum of the first n terms of the
above sequence for 0≤n≤10 Graph 1) Relation between Sn and n

2. Hyohyun Lee
2
Consider another sequence of terms where x = 1 and a = 3,
1,
(ln3)
1
,
(ln3)2
2 x 1
,
(ln3)3
3 x 2 x 1
…
As it is shown in Graph 1, Graph 2 also shows the similarity in the shape with the
function of log or ln. However, unlike the Graph 1, the location where the line bends comes
later, which means that the graph has longer increasing period than the Graph 1 has.
As n approaches ∞, the value of 𝑆 𝑛 approaches 3. Here, it can be known that the a-
value, which is 3, is an asymptote as shown in Graph 1. In addition, from the Table 2, the
value of each term is getting smaller and smaller as it goes infinitely.
0
1
2
3
4
0 2 4 6 8 10 12
Sn
n
Relation between Sn and n
Sum
Table 2) Sum of the first n terms of
the above sequence for 0≤n≤10
Graph 2) Relation between Sn and n

3. Hyohyun Lee
3
Now consider a general sequence where x =1,
1,
(ln 𝑎)
1
,
(ln 𝑎)2
2 x 1
,
(ln 𝑎)3
3 x 2 x 1
…
Calculate the sum Sn of the first n terms of this general sequence for 0 ≤ 𝑛 ≤ 10 for
different values of a.
Consider sequence of terms where x = 1 and a = 5,
1,
(ln5)
1
,
(ln 5)2
2 x 1
,
(ln5)3
3 x 2 x 1
…
Graph 3 also appears as similar as the Graph 1 or Graph 2. It starts from (0, 1) and
the a-value is an asymptote again. As n goes infinitely, Sn approaches 5, the a-value, and does
not touch y = 5.
More interestingly, even though the shape is similar with other graphs, the increasing
period in Graph 3 seems much longer than previous ones.
Table 3) Sum of the first n terms of
the above sequence for 0≤n≤10
Graph 3) Relation between Sn and n

4. Hyohyun Lee
4
Consider sequence of terms where x = 1 and a = 10,
1,
(ln10)
1
,
(ln 10)2
2 x 1
,
(ln 10)3
3 x 2 x 1
…
Like in any other graphs, in Graph 4, the a-value, 10, is an asymptote and the graph
does not touch the asymptote. As a-value is getting bigger, the increasing period at the
beginning of the graph is getting longer and longer.
Graph 4) Relation between Sn and n
Table 4) Sum of the first n terms of
the above sequence for 0≤n≤10

5. Hyohyun Lee
5
Consider sequence of terms where x = 1 and a = 20,
1,
(ln20)
1
,
(ln 20)2
2 x 1
,
(ln 20)3
3 x 2 x 1
…
Like in any other graphs, in Graph 5, the a-value, 20, is an asymptote and the graph
does not touch the asymptote. As a-value is getting bigger, the increasing period at the
beginning of the graph is getting longer and longer.
Table 5) Sum of the first n terms of
the above sequence for 0≤n≤10
Graph 5) Relation between Sn and n

6. Hyohyun Lee
6
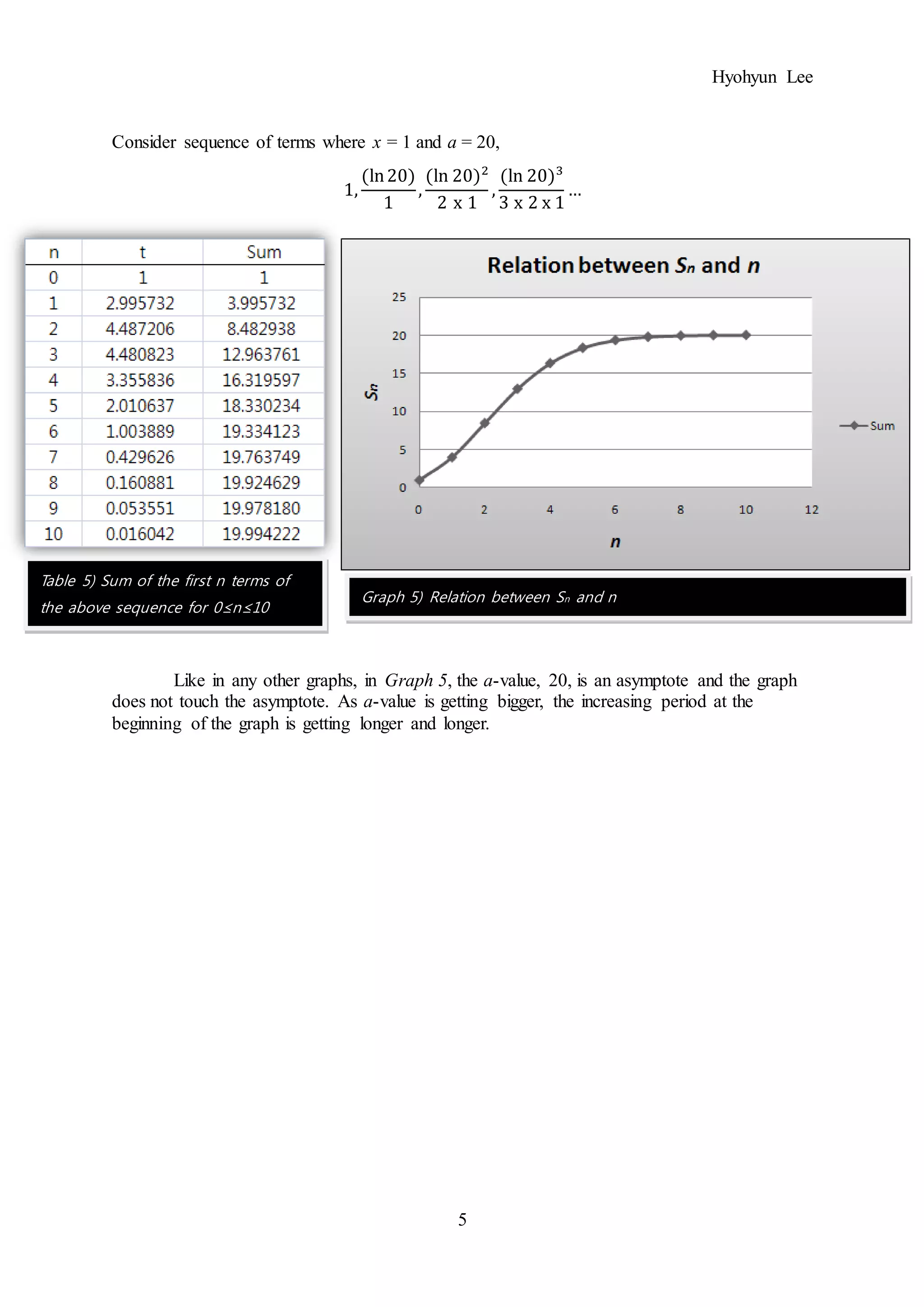
Consider sequence of terms where x = 1 and a = 100,
1,
(ln 100)
1
,
(ln100)2
2 x 1
,
(ln 100)3
3 x 2 x 1
…
Like in any other graphs, in Graph 6, the a-value, 100, is an asymptote and the graph
does not touch the asymptote. As a-value is getting bigger, the increasing period at the
beginning of the graph is getting longer and longer.
[General Statement]
From six graphs and tables, it is obvious that the all a-values become asymptotes in
all graphs when x = 1. To be more specific, when x-value is 1, all graphs do not go more than
the a-value. Additionally, as a-value is getting bigger, the point where the graph bends comes
later, which means that the period until the graph reaches almost the asymptote is longer and
longer.
Therefore, as the n goes infinitely, the value of Sn approaches the asymptote, which is
set by a-value.
Table 6) Sum of the first n terms of
the above sequence for 0≤n≤10
Graph 6) Relation between Sn and n

7. Hyohyun Lee
7
Define 𝑇𝑛(𝑎, 𝑥) as the sum of the first n terms, for various values of a and x.
e.g. 𝑇9(2,5) is the sum of the first nine terms when a = 2 and x = 5.
Let a = 2. Calculate 𝑇9(2, 𝑥) for various positive values of x.
Consider sequence of terms where x = 4 and a = 2,
1,
(4 ln2)
1
,
(4 ln2)2
2 x 1
,
(4ln 2)3
3 x 2 x 1
…
The shape of Graph 7 seems similar to that of previous ones. Additionally, the graph
starts from (0, 1) like other graphs. It also has an asymptote, which is y = 16, but in this graph,
it seems that the a-value and the asymptote are not the same; a = 2 and the asymptote is
y = 16.
Table 7) Sum of the first 9 terms of
the above sequence
Graph 7) Relation between T9(2, 4) and x

8. Hyohyun Lee
8
Consider sequence of terms where x = 9 and a = 2,
1,
(9 ln2)
1
,
(9 ln2)2
2 x 1
,
(9ln 2)3
3 x 2 x 1
…
Here, it is clear that the shape of Graph 7 and that of Graph 8 are totally different.
This is more like an exponential graph while the previous ones are similar to the graph of ln
or log. However, Graph 8 does not have vertical asymptote while most exponential graphs
have vertical asymptotes.
Table 8) Sum of the first 9 terms of
the above sequence
Graph 8) Relation between T9(2, 9) and x

9. Hyohyun Lee
9
Consider sequence of terms where x = 15 and a = 2,
1,
(15 ln2)
1
,
(15 ln2)2
2 x 1
,
(15ln 2)3
3 x 2 x 1
…
In comparison to Graph 8, Graph 9 is more like an exponential graph. Therefore, it
can be said that as the x-value is getting bigger with fixed a-value, the shape of graph
becomes more like that of an exponential graph. However, there will not be any vertical
asymptote in this graph because the number is continuously added to the previous number. So,
it will grow infinitely as n goes ∞.
Table 9) Sum of the first 9 terms of
the above sequence
Graph 9) Relation between T9(2, 15) and x

10. Hyohyun Lee
10
Let a = 3. Calculate 𝑇9(3, 𝑥) for various positive values of x.
Consider sequence of terms where x = 4 and a = 3,
1,
(4 ln3)
1
,
(4 ln3)2
2 x 1
,
(4ln 3)3
3 x 2 x 1
…
Graph starts from (0, 1) like other graphs. It also has an asymptote, which is y = 80,
but in this graph, it seems that the a-value and the asymptote are not the same; a = 3 and the
asymptote is y = 80. And compared to other graphs, this graph is a little flat.
Table 10) Sum of the first 9 terms of
the above sequence
Graph 10) Relation between T9(3, 4) and x

11. Hyohyun Lee
11
Consider sequence of terms where x = 9 and a = 3,
1,
(9 ln3)
1
,
(9 ln3)2
2 x 1
,
(9ln 3)3
3 x 2 x 1
…
Here, it is clear that the shape of Graph 10 and that of Graph 11 are totally different.
This is more like an exponential graph. However, Graph 11 does not have vertical asymptote
while most exponential graphs have vertical asymptotes. It may have horizontal asymptote
later when the value of n becomes bigger and bigger.
Table 11) Sum of the first 9 terms of
the above sequence
Graph 11) Relation between T9(3, 9) and x

12. Hyohyun Lee
12
Consider sequence of terms where x = 15 and a = 3,
1,
(15 ln3)
1
,
(15 ln3)2
2 x 1
,
(15ln 3)3
3 x 2 x 1
…
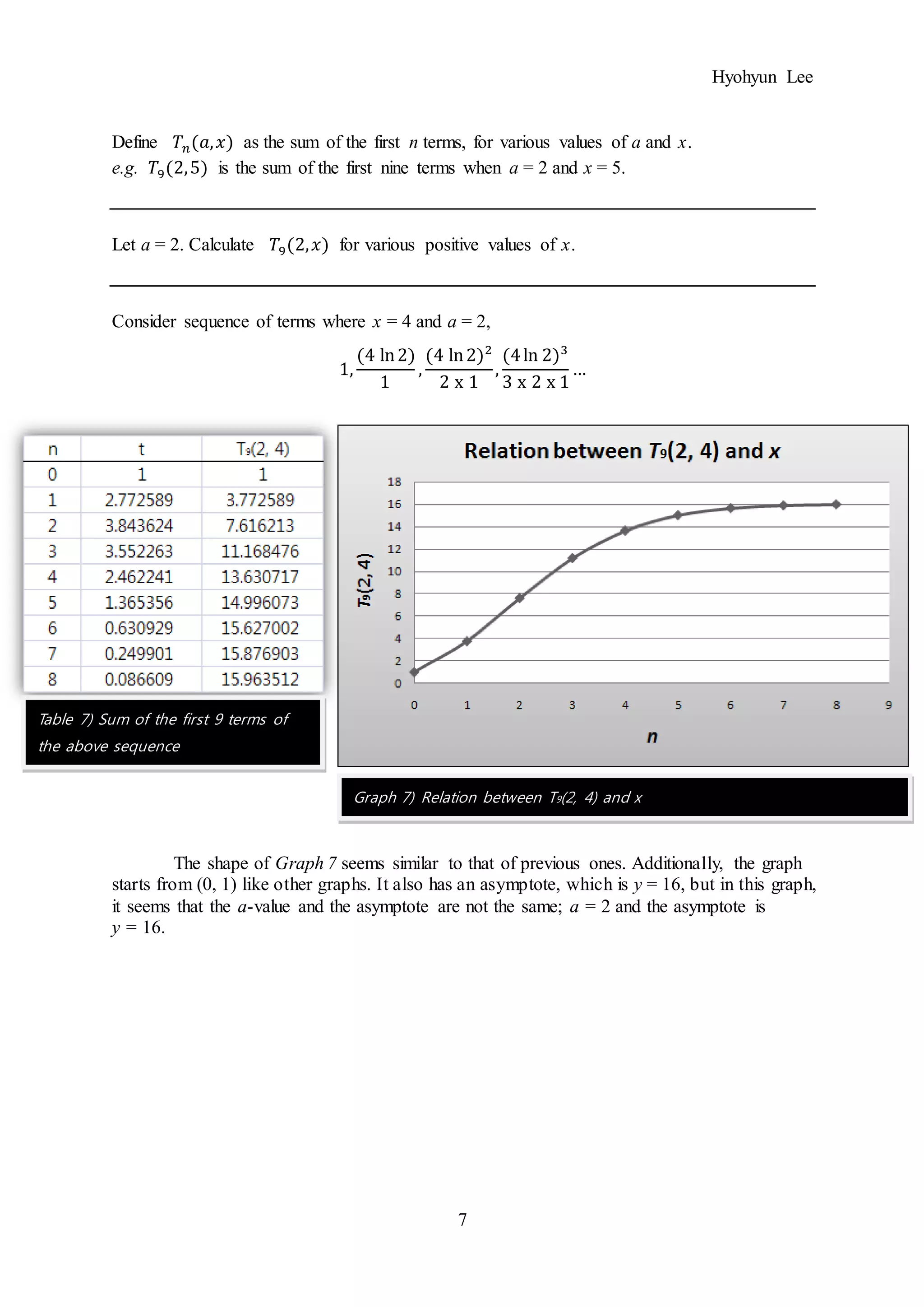
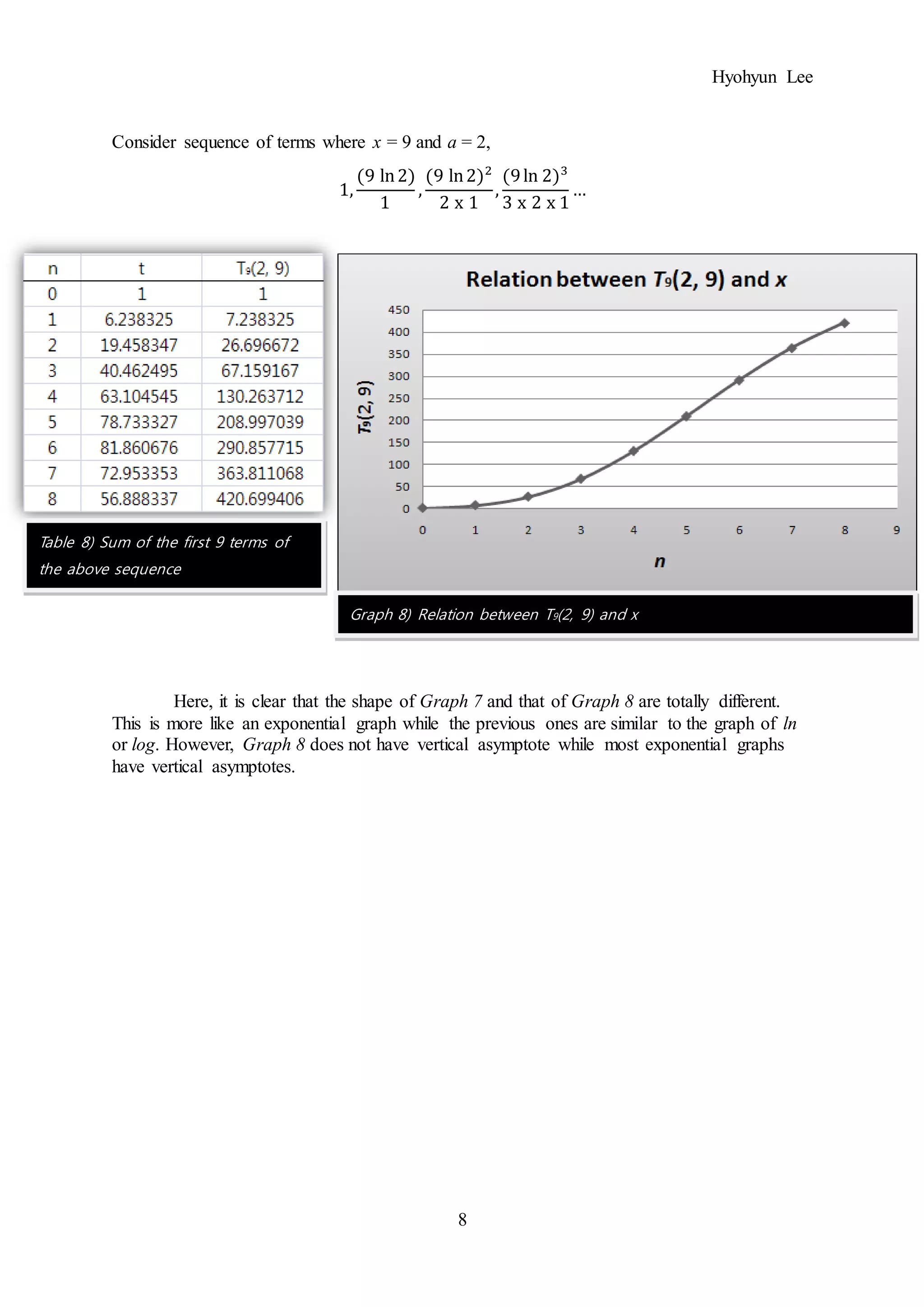
In comparison to Graph 11, Graph 12 is more like an exponential graph. Therefore, it
can be said that as the x-value is getting bigger with fixed a-value, the shape of graph
becomes more like that of an exponential graph. However, there will not be any vertical
asymptote in this graph because the number is continuously added to the previous number. So,
it will grow infinitely as n goes ∞.
[General Statement]
When the a-value is fixed and only x-values are changeable, as the x-value is getting
bigger, the graph becomes more similar to an exponential graph. In addition, when the x-
value is small, the graph appears a little flat compared to other graphs.
Therefore, as n approaches ∞, 𝑇𝑛(𝑎, 𝑥) keeps increasing and may reach its
asymptote at the point of a really big value.
Table 12) Sum of the first 9 terms of
the above sequence
Graph 12) Relation between T9(3, 15) and x

13. Hyohyun Lee
13
Test the validity of the general statement with other values of a and x.
Consider sequence of terms where x = 17 and a = 6,
1,
(17 ln6)
1
,
(17 ln6)2
2 x 1
,
(17ln 6)3
3 x 2 x 1
…
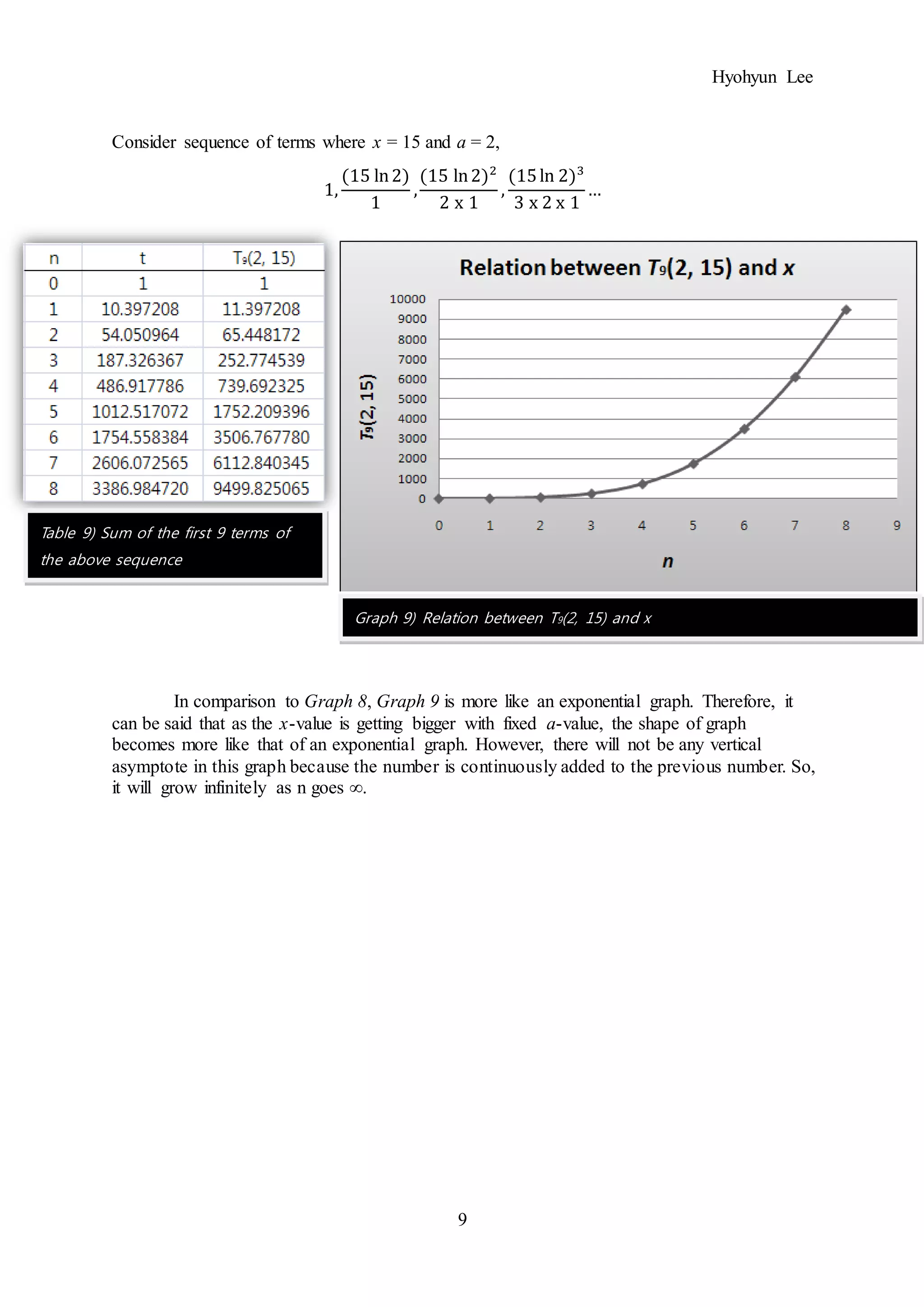
If the general statement is correct, this equation should have a graph with the shape of an
exponential graph.
As the value of x is big (x = 17), the shape of Graph 13 is similar to that of an
exponential graph.
[Scope and/or limitations of the general statement]
The first limitation of the general statement is that either x-value or a-value has to be
fixed in order to see what happened to each graph. So, when two of the values are changed, it
is hard to determine what has been different from other graphs.
The second limitation is that in the second general statement, it is vague that ‘as n
approaches ∞, 𝑇𝑛(𝑎, 𝑥) keeps increasing and may reach its asymptote at the point of a really
big value.’ It has not been proved that where it meets the asymptote and that whether this
graph really has an asymptote or not. Thus, the words ‘may reach its asymptote’ well show
the limitations of the general statement.
[How I arrived at the general statement]
By observing all graphs that I came up with, I could arrive at the general statement
easily. First, I tried to find some similarities between two graphs so that I could make sure the
same aspect could adjust to other graphs. And then, I tried to find out some differences such
as the shape of graphs or the asymptote. Those differences show how each graph is different
from each other and how each value affects graphs.
Table 13) Sum of the first 9 terms of the
above sequence
Graph 13) Relation between T9(6, 17) and x