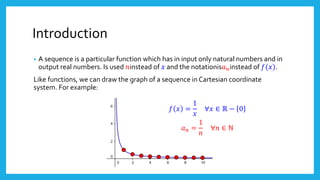
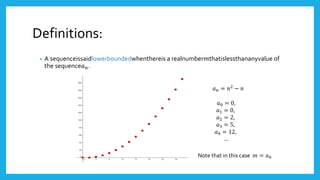
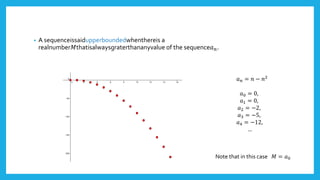
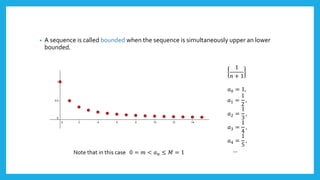
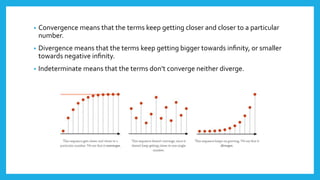
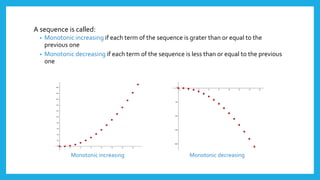
The document defines key concepts related to sequences: - A sequence is a function with natural numbers as inputs and real numbers as outputs. Sequences can be bounded, meaning all terms fall within a certain range, or unbounded. - Sequences can converge, meaning the terms get closer to a limit, or diverge, meaning the terms approach positive or negative infinity. - A sequence is monotonically increasing if each term is greater than or equal to the previous one, and monotonically decreasing if each term is less than or equal to the previous one. - A sequence converges to a value L if, given any small positive number ε, there exists an N such that all terms after N are within

1. THE SEQUENCES
Introduction

2. Introduction
• A sequence is a particular function which has in input only natural numbers and in
output real numbers. Is used 𝑛instead of 𝑥 and the notationis𝑎 𝑛instead of 𝑓(𝑥).
Like functions, we can draw the graph of a sequence in Cartesian coordinate
system. For example:
𝑓 𝑥 =
1
𝑥
∀𝑥 ∈ ℝ − 0
𝑎 𝑛 =
1
𝑛
∀𝑛 ∈ ℕ

3. Definitions:
• A sequenceissaidlowerboundedwhenthereis a realnumber𝑚thatislessthananyvalue of
the sequence𝑎 𝑛.
𝑎 𝑛 = 𝑛2
− 𝑛
𝑎0 = 0,
𝑎1 = 0,
𝑎2 = 2,
𝑎3 = 5,
𝑎4 = 12,
…
Note that in this case 𝑚 = 𝑎0

4. • A sequenceissaidupperboundedwhenthereis a
realnumber𝑀thatisalwaysgraterthananyvalue of the sequence𝑎 𝑛.
𝑎 𝑛 = 𝑛 − 𝑛2
𝑎0 = 0,
𝑎1 = 0,
𝑎2 = −2,
𝑎3 = −5,
𝑎4 = −12,
…
Note that in this case 𝑀 = 𝑎0

5. • A sequence is called bounded when the sequence is simultaneously upper an lower
bounded.
1
𝑛 + 1
𝑎0 = 1,
𝑎1 =
1
2
,
𝑎2 =
1
3
,
𝑎3 =
1
4
,
𝑎4 =
1
5
,
…Note that in this case 0 = 𝑚 < 𝑎 𝑛 ≤ 𝑀 = 1

6. A sequence is called:
• Monotonic increasing if each term of the sequence is grater than or equal to the
previous one
• Monotonic decreasing if each term of the sequence is less than or equal to the previous
one
Monotonic increasing Monotonic decreasing

7. LIMIT OF SEQUENCES
How is the overall graphic of a sequence?
In studying a sequence we may be interested in what happens to the terms
as we increase more and more the 𝑛 value.

8. • Convergence means that the terms keep getting closer and closer to a particular
number.
• Divergence means that the terms keep getting bigger towards infinity, or smaller
towards negative infinity.
• Indeterminate means that the terms don’t converge neither diverge.

9. Convergence definition
• When 𝑛 becomes bigger and bigger, we say that a sequence 𝑎 𝑛converges to a
valuey if for any tiny positive number 𝜀 you can choose, exists a natural number 𝑁
so that 𝑎 𝑁, 𝑎 𝑁+1, 𝑎 𝑁+2, … are all between y − 𝜀 and y + 𝜀.

10. Divergence definition
When 𝑛 becomes bigger and bigger, we say that a sequence 𝑎 𝑛diverges to
+/−∞ when for any positive number 𝑀 you choose, exists a natural number 𝑁 so
that 𝑎 𝑁, 𝑎 𝑁+1, 𝑎 𝑁+2, … are all bigger than 𝑀 (divergence toward +∞) or are all less
than – 𝑀 (divergence toward −∞)
𝑎 𝑛 = 𝑛3
𝑀 = 2500

11. Created by
Erasmus+ M.A.T.H.S.
Geogebra team students
Giovanni Montanari
Simone Mattioli
Jernie Pasahol
I.T.T.S. «A.Volta» Perugia
2015/2016