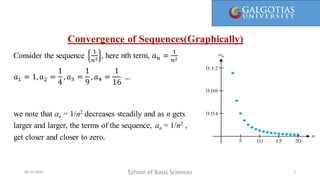
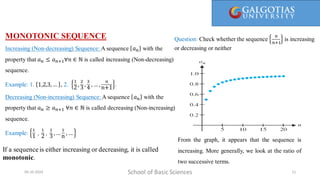
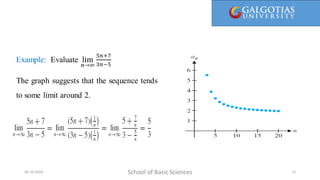
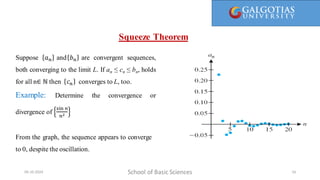
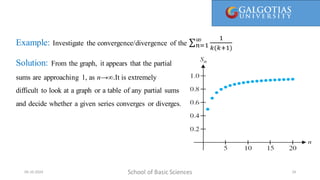
The document covers concepts related to sequences and their convergence, as well as infinite series. It explains definitions, examples, and properties of various types of sequences, including bounded and monotonic sequences, and includes methods for determining convergence or divergence of both sequences and series. Key takeaways include the uniqueness of limits for convergent sequences and the application of the nth-term test for series divergence.