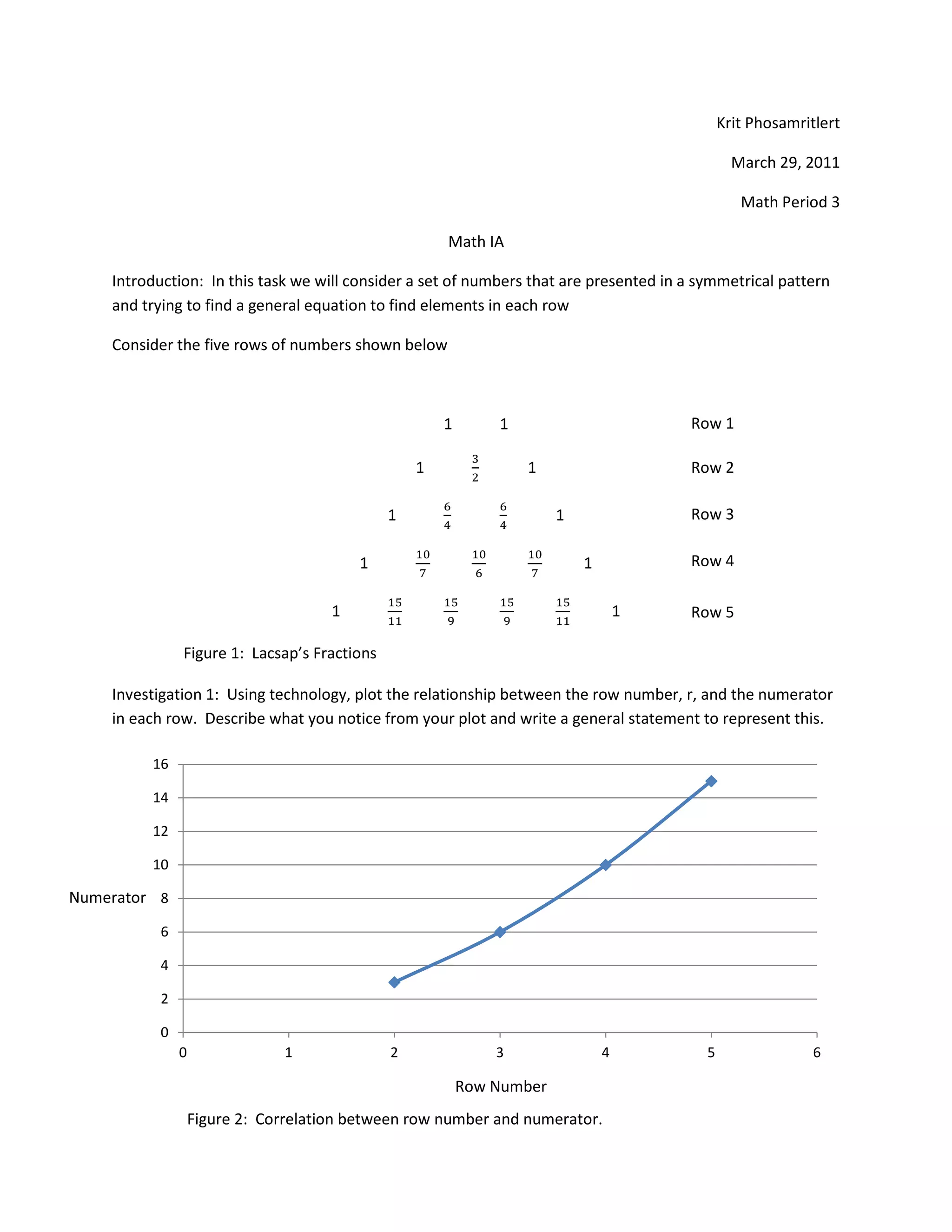
This document presents an investigation into Lacsap's Fractions, a symmetrical pattern of numbers. The author derives a general equation to calculate any element in any given row. They plot the relationship between row number and numerator, noticing the numerators increase by one more than the previous term. This leads to an equation relating row number r and numerator. By observing patterns in the differences between numerators and denominators, they extend the equation to calculate any element Er(n). They validate the general equation by calculating additional rows. The limitations are it cannot calculate the first row or elements outside the range from 1 to r-1.

1. Math IA
IB Math SL
Period 3
By: Krit Phosamritlert

2. Krit Phosamritlert
March 29, 2011
Math Period 3
Math IA
Introduction: In this task we will consider a set of numbers that are presented in a symmetrical pattern
and trying to find a general equation to find elements in each row
Consider the five rows of numbers shown below
1 1 Row 1
3
2
1 1 Row 2
6 6
4 4
1 1 Row 3
10 10 10
7 6 7
1 1 Row 4
15 15 15 15
11 9 9 11
1 1 Row 5
Figure 1: Lacsap’s Fractions
Investigation 1: Using technology, plot the relationship between the row number, r, and the numerator
in each row. Describe what you notice from your plot and write a general statement to represent this.
16
14
12
10
Numerator 8
6
4
2
0
0 1 2 3 4 5 6
Row Number
Figure 2: Correlation between row number and numerator.

3. By looking at the graph, the numerator of each row is consistent when all the “1” are discarded. The
numerator of the sixth row can be found by observing the sequence of the numerators in each row.
Since all the “1” are discarded the sequence actually starts at row 2 and not at row 1. The sequences of
numerators are 3, 6, 10, and 15. As one can observe the numerators are increasing by one more than
the previous term as from 3 to 6 the numerator is increased by 3 and from 6 to 10 the numerator is
increase by 4 and so on. This can then be formulated into an equation using the row number as a
variable to calculate the numerator. Using the row number as the base to find the numerator, one can
observe that to get from 2 (row number 2) to 3 (numerator of row 2) the row number is multiplied by
1.5. In the next row, to get from 3 (row number 3) to 6 (numerator of row 3) the row number is
multiplied by 2. In row four, to get from 4 (row number) to 10 (numerator of row 4) the row number is
multiplied by 2.5. From this observation I observed that to get the numerator from the row number
each row is multiplied by a certain number that is 0.5 more than the previous row. This can then be
formulated into an equation where each row number (r) is multiplied by the row divided by 2 plus 0.5 as
������
shown below.
������( + 0.5)
2
Equation 1
This equation was found by looking at each row number and the number that each row number is
multiplied by to get the numerator. For example for row 2 the row number is multiplied by 1.5 and for
row 3 the row number is multiplied by 2. One can see that if the row number is divided by 2 and 0.5 was
added to the result, the outcome is the number that is multiplied with the row number to find the
numerator.
Investigation 2: Describe how to find the numerator of the sixth row
To find the numerator of the sixth row 6 is substituted for r and equation 1 was used as shown below
6
6 � + 0.5� = 21
2
Investigation 3: Find the sixth and seventh rows. Describe any patterns you used. Find the general
statement for Er(n).
To find each element in each row, the denominator of each element must be found in addition to the
numerator of each row. To find the denominator of each element in each row the relationship between
the numerator and the denominator of each row was observed. Once again all the “1” are discarded
since the “1” were discarding during the calculation of the numerator also. This also limits the number
of elements in a certain row to be r – 1 (i.e. for row 2 there is only 1 element after the “1” are
discarded). To find the denominator of each element, the denominator of the first element of each row
was observed first as shown in the figure below.

4. 1 1 Row 1
3
2
1 1 Row 2
6 6
4 4
1 1 Row 3
10 10 10
7 6 7
1 1 Row 4
15 15 15 15
11 9 9 11
1 1 Row 5
Figure 3: Correlation between numerator and denominator of element 1
The difference between the numerator and the denominator was observed for element 1 (highlighted
yellow). The difference was recorded as 1, 2, 3, and 4 for row 2, 3, 4, and 5 respectively. Using the
numerator as the base for finding the denominator the initial equation was formed as shown below
������������������������������������������������������ − (������) = ������������������������������������������������������������������ Equation 2
This is where x is the difference between the numerator and denominator and is formed by using the
row number and the element number. Knowing that the difference of the denominator of element one
increases by 1 every consecutive row, a statement can be made that the numerator minus 1 times the
row number minus 1 equals the denominator of element 1 as shown below
������������������������������������������������������ − 1(������ − 1) = ������������������������������������������������������������������ Equation 3
Now the second of each row was observed (highlighted blue). The difference between the numerator
and the denominator of the second element was recorded as 2, 4 and, 6. For element two, the
difference between the numerator and the denominator increases by 2 every consecutive row. This can
then be made into a statement that the numerator minus 2 times the row number minus 2 equals the
denominator of element 2 as shown below
������������������������������������������������������ − 2(������ − 2) = ������������������������������������������������������������������ Equation 4
Now that two equations have been formulated for element one and element two of each row, the
similarity between the two equations was observed. In equation 3 the “1” in the x part of the equation
is equivalent to the element number and as for equation 4 the “2” in the x part of the equation is also
equivalent to the element number. The x part of the equation can now be substituted by the element
number, n, to form a general statement as shown below
������������������������������������������������������ − ������(������ − ������) = ������������������������������������������������������������������
or
������ � + 0.5� − ������(������ − ������) = ������������������������������������������������������������������
������
2
Equation 5

5. To find the sixth and seventh row, the general statement of the numerator and the denominator must
������
be combined to create the general statement for the element, Er(n), as shown below
������(2 + 0.5)
������������ (������) = ������
������ �2 + 0.5� − ������(������ − ������)
Equation 6
Using this general statement for Er(n), each element can then be found by substituting r for the row
number, starting off at r = 2, and n for the element number, stating off at n = 1 up to n = r – 1 according
to the limitations. Using this equation the sixth row is as shown below
������6 (1) = ������6 (5) =
6( +0.5) 6( +0.5)
6 6
2 2
6� +0.5� − 1(6−1) 6� +0.5� − 5(6−5)
6 … 6
2 2
Using the calculations above the sixth row comes out to be as shown below
21 21 21 21 21
16 13 12 13 16
Knowing that the “1” in each row is discarded while doing the calculations the “1” must be added back
into the row at the beginning and at the end after doing the calculation to get the entire row as shown
below
21 21 21 21 21
Row 6
16 13 12 13 16
1 1
The seventh row is also found using the same equation used to find the sixth row (equation 6) as shown
below
������7 (1) = ������7 (6) =
7( +0.5) 7( +0.5)
7 7
2 2
7� +0.5� − 1(7−1) 7� +0.5� − 6(7−6)
7 … 7
2 2
Using the calculations above the seventh row comes out to be as shown below
28 28 28 28 28 28
21 18 16 16 18 21
Knowing that the “1” in each row is discarded while doing the calculations the “1” must be added back
into the row at the beginning and at the end after doing the calculation to get the entire row as shown
below
28 28 28 28 28 28
21 18 16 16 18 21
1 1 Row 7
Investigation 4: Test validity of the general statement by finding additional rows
By using the same method used to find the sixth and seventh row, the eighth, ninth, and tenth row were
found to validate the general statement made as shown below

6. ������8 (1) = ������8 (7) =
8( +0.5) 8( +0.5)
8 8
2 2
8� +0.5� − 1(8−1) 8� +0.5� − 7(8−7)
8 … 8
2 2
������9 (1) = ������9 (8) =
9( +0.5) 9( +0.5)
9 9
2 2
9� +0.5� − 1(9−1) 9� +0.5� − 8(9−8)
9 … 9
2 2
10(1) = ������10 (9) =
10( +0.5) 10( +0.5)
10 10
2 2
10� +0.5� − 1(10−1) 10� +0.5� − 9(10−9)
10 … 10
2 2
Using these equations the eighth, ninth, and tenth row comes out to be as shown below
36 36 36 36 36 36 36
29 24 21 20 21 24 29
45 45 45 45 45 45 45 45
37 31 27 25 25 27 31 37
55 55 55 55 55 55 55 55 55
46 39 34 31 30 31 34 39 46
Knowing that the “1” in each row is discarded while doing the calculations the “1” must be added back
into the row at the beginning and at the end after doing the calculation to get the entire row as shown
below
36 36 36 36 36 36 36
29 24 21 20 21 24 29
1 1 Row 8
45 45 45 45 45 45 45 45
37 31 27 25 25 27 31 37
1 1 Row 9
55 55 55 55 55 55 55 55 55
46 39 34 31 30 31 34 39 46
1 1 Row 10
Investigation 5: Discuss the scope and/or limitations of the general statement
During the calculation of the numerator and the denominator of each element, the “1” at the beginning
and at the end of each row were discarded before making the calculations. This is a limitation to the
application for using the general equation that was derived to find a specific element in a specific row.
Since the first row is only comprised of “1” and the “1” are discarded, the general equation cannot be
used to calculate the elements of the first row. Also due to this discarding of the “1” the number of
element in each row is also decreased by 2 therefore the element number does not start at 0 (the
beginning “1”) but starts at 1 and does not end at the row number but at the row number – 1 (due to
the discarding of the “1” at the end of the row). This means that to calculate a specific element in a
specific row r must be greater than or equal to 2 and n must be greater than or equal to 1 and less than
or equal to row – 1 of that particular row.

7. Academic Honest
“I, the undersigned, hereby declare that the following assignment is all my own work and that I worked
independently on it.”
“In this assignment, I used Microsoft Excel to draw my graphs.”
Krit Phosamritlert