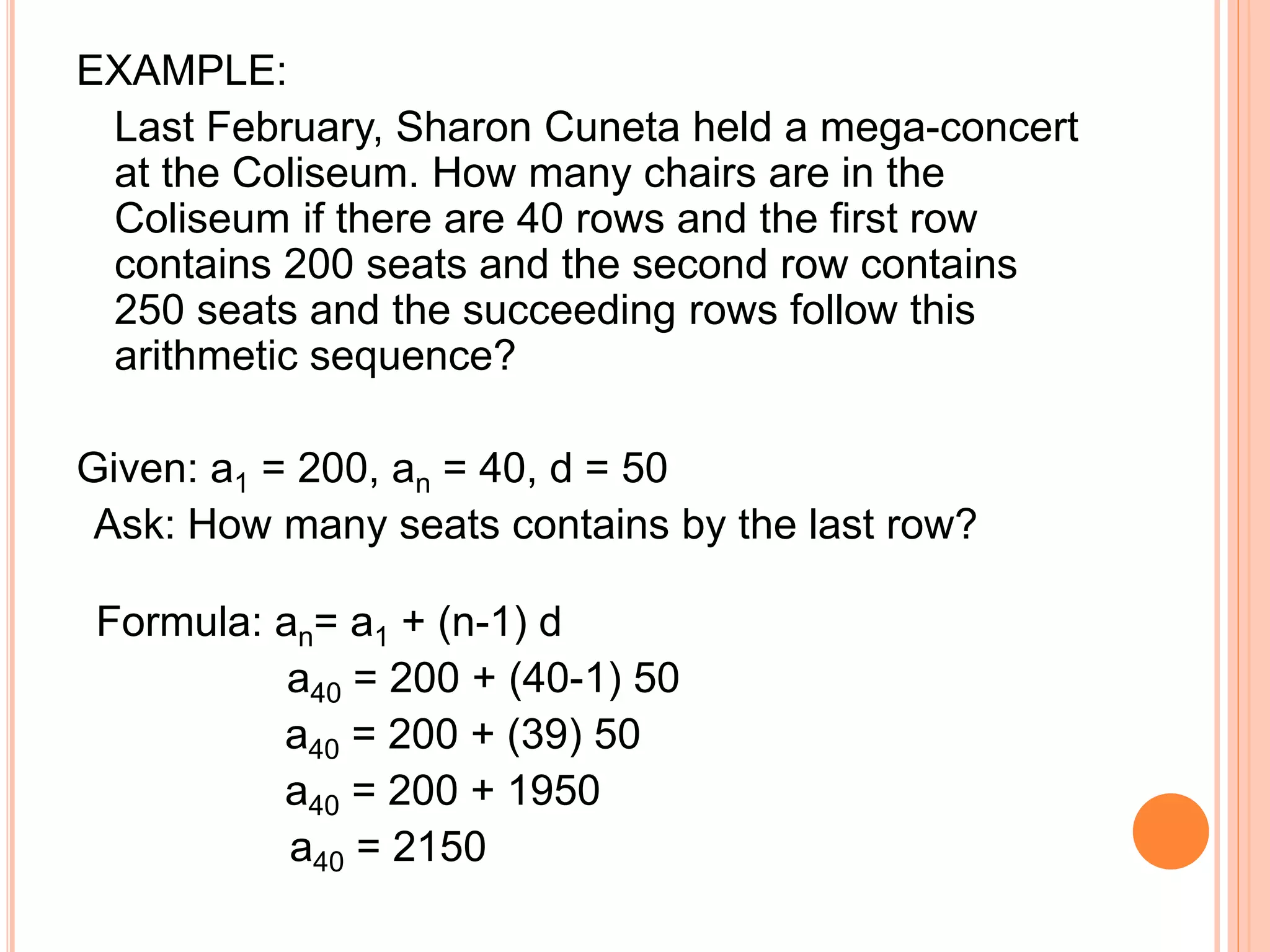An arithmetic sequence is a sequence where each term after the first is obtained by adding a constant value, called the common difference, to the preceding term. The document provides examples of arithmetic sequences and explains how to identify them and calculate the nth term using formulas like an = a1 + (n-1)d, where a1 is the first term, d is the common difference, and n is the term number. It also shows how to use these concepts and formulas to solve problems involving finding terms and sums of arithmetic sequences.

1. Prepared by:
Kevin P. Gabisay
Joan C. Tonacao
Jezreel A. Carbonquillo
Arithmetic Sequence

2. Learning Objectives:
I can identify arithmetic sequences
I can calculate the nth term in arithmetic
sequences
I can find the number of terms in an
arithmetic sequences

3. Arithmetic Sequence
-is a sequence where each new term after the first is
obtained by adding a constant d, to the preceding term.
Identifying an Arithmetic Sequence
Sequences of numbers that follow a pattern of
adding a fixed number from one term to the next are
called arithmetic sequences. The following sequences
are arithmetic sequences:
Example A: 5 , 8 , 11 , 14 , 17 , ...
For Example A, if we add 3 to the first number we
will get the second number. This works for any pair of
consecutive numbers. The second number plus 3 is the
third number:
8 + 3 = 11, and so on.

4. Example B:
Write down the first 5 term of arithmetic
sequence with first term 8 and common difference
of 7.
Answer:
8, 15, 22, 29, 36
Because this sequence behave according to
this simple rule of adding a constant number to one
term to get to another, they are called arithmetic
sequence. So that we can examine these sequence
to greater depth, we must know that the fixed
numbers that bind each sequence together are
called the common difference. Sometimes
mathematicians use the letter d when referring to
these types of sequence.

5. Calculating the nth Term
The formula for finding any term of an
arithmetic sequence is an=a+ (n-1)d where a is the
first term of the sequence, d is the common
difference, and n is the number of the term to find.

6. EXAMPLE:
Last February, Sharon Cuneta held a mega-concert
at the Coliseum. How many chairs are in the
Coliseum if there are 40 rows and the first row
contains 200 seats and the second row contains
250 seats and the succeeding rows follow this
arithmetic sequence?
Given: a1 = 200, an = 40, d = 50
Ask: How many seats contains by the last row?
Formula: an= a1 + (n-1) d
a40 = 200 + (40-1) 50
a40 = 200 + (39) 50
a40 = 200 + 1950
a40 = 2150

7. There is also another formula to use:
an = dn + the number before the first term
where: d – is the difference between the first term
an/n – the term that is ask to find out
Base on the given problem:
Given: a1 = 200, an /n = 40, d = 50
Formula: an = dn + the number before the first term
a40 = 50 (40) + 150
a40 = 2000 + 150
a40 = 2150

8. Evaluation:
Direction: Solve what is ask?
1. Write down the 50th and 60th terms of
arithmetic sequence 7,15,23,…
2. Find the sum of all integers from 1 to 1,000.
3. Find the sum of the first 100 terms of even
integers.
4. Write down the 101th term of arithmetic
sequence 2/15,7/15,12/15,…
5. An arithmetic sequence has first term 4 with
the difference of ½. Find the sum of first 120
terms.

9. References:
 http://www.mathguide.com/lessons/SequenceArithmeti
c.html
 Exploring Mathematics II (Intermediate Algebra), by
Orlando A. Oronce and Marilyn O. Mendoza