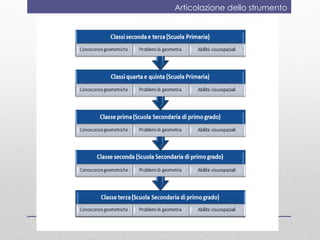
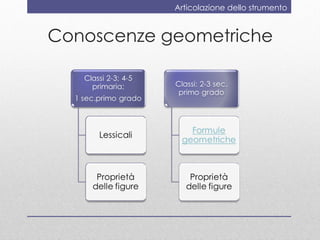
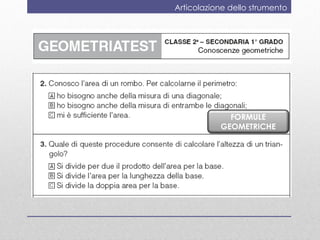
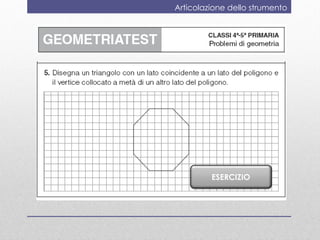
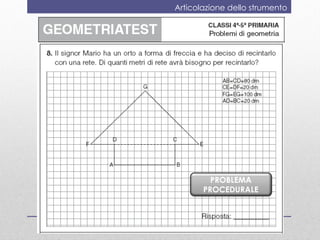
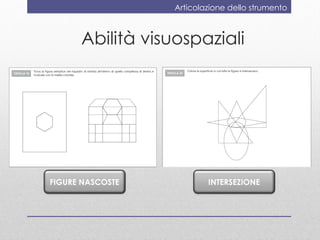
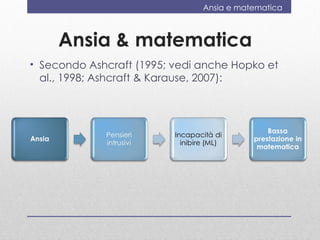
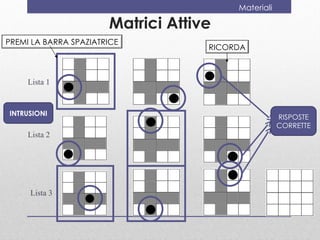
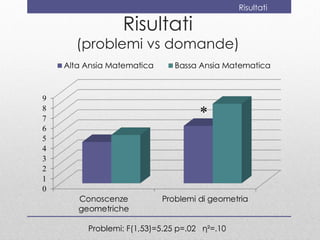
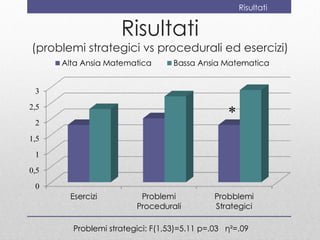
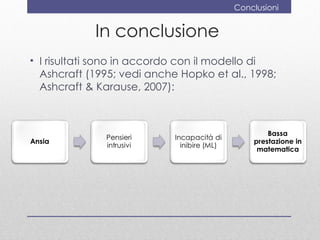
Il documento discute la valutazione dell'apprendimento della geometria nei bambini dai 4 ai 6 anni, evidenziando conoscenze e abilità chiave come la denominazione e la classificazione delle figure. Viene presentato uno strumento di valutazione, il 'geometriatest', e una ricerca sull'ansia per la matematica che mostra come i bambini con alta ansia affrontano difficoltà nei problemi geometrici strategici. Si conclude suggerendo l'importanza di valutare l'ansia matematica e di far vivere esperienze di successo in geometria.