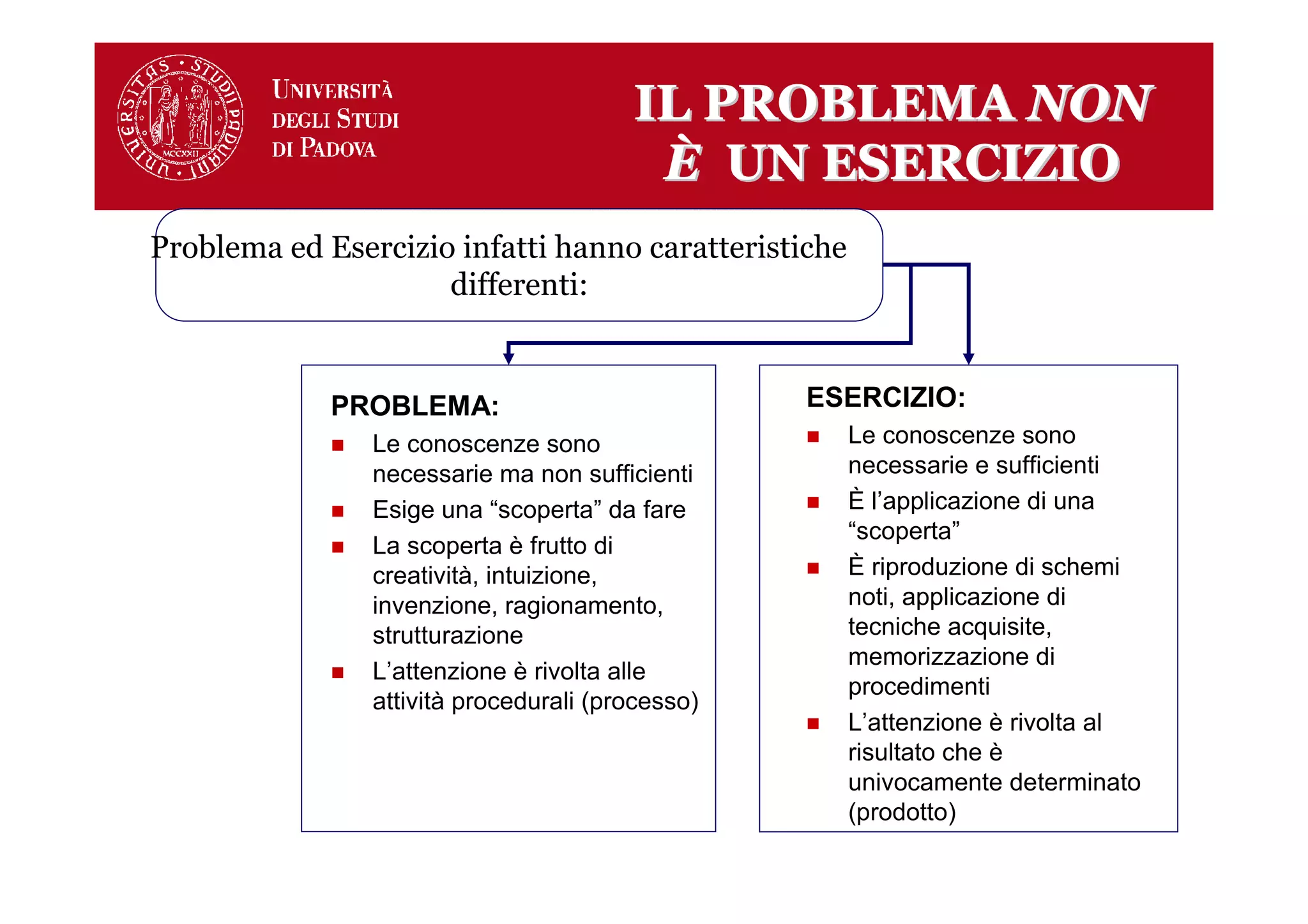
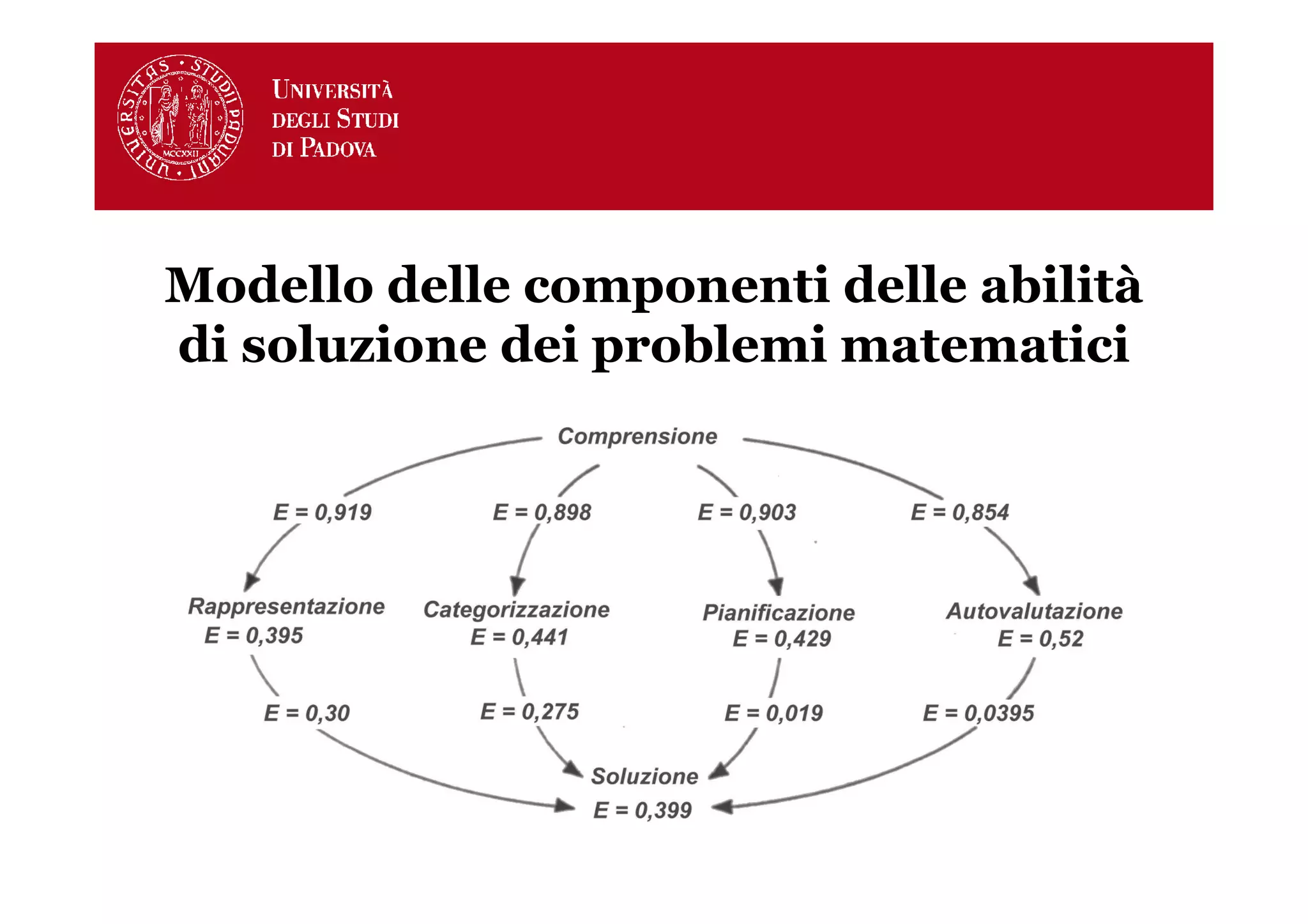
Il documento analizza il processo di risoluzione dei problemi in geometria, evidenziando le differenze tra problemi ed esercizi e le fasi in cui possono sorgere difficoltà. Viene presentato un modello delle componenti delle abilità di soluzione dei problemi e classificati vari tipi di problemi, con esempi pratici. Infine, si suggeriscono programmi di potenziamento e risorse per approfondire le difficoltà nell'apprendimento della geometria.

1. Problemi ed Esercizi
Apprendere in geometria
Prof. Daniela Lucangeli
8 maggio 2012, III Seminario di studio
“APPRENDERE LA GEOMETRIA”

2. Un esempio
divertente …

3. La soluzione dei problemi
rappresenta un
Processo dinamico:
elaborazione cognitiva
complessa

4. IL PROBLEMA NON
È UN ESERCIZIO
Problema ed Esercizio infatti hanno caratteristiche
differenti:
PROBLEMA: ESERCIZIO:
Le conoscenze sono Le conoscenze sono
necessarie ma non sufficienti necessarie e sufficienti
Esige una “scoperta” da fare È l’applicazione di una
“scoperta”
La scoperta è frutto di
creatività, intuizione, È riproduzione di schemi
invenzione, ragionamento, noti, applicazione di
strutturazione tecniche acquisite,
memorizzazione di
L’attenzione è rivolta alle
procedimenti
attività procedurali (processo)
L’attenzione è rivolta al
risultato che è
univocamente determinato
(prodotto)

5. In quali fasi di risoluzione del
problema si può incontrare
difficoltà?
1. Comprensione delle informazioni presenti nel
COMPRENSIONE
problema e delle loro relazioni
2. Rappresentazione delle informazioni mediante uno
schema in grado di strutturarle ed integrarle
3. Categorizzazione del problema in base alla struttura
profonda (operazioni necessarie per risolvere il
problema stesso)
PRODUZIONE
4. Pianificazione delle procedure
5. Monitoraggio e Valutazione

6. Modello delle componenti delle abilità
di soluzione dei problemi matematici

7. Classificazione dei
problemi
• Problemi procedurali richiedono che il bambino
ricordi la procedura (o formula) per ottenere un
dato
• I problemi strategici non offrono subito tutti i
dati necessari per applicare la procedura o
semplicemente per rispondere al problema,
bisogna individuare i dati usando una strategia
che deve essere scoperta dal bambino.

8. Es. Problemi vs
Esercizi
• Zia Maria ha un orto a forma di triangolo
isoscele. Un lato misura 5 m e i due lati uguali
PROBLEMA
PROCEDURALE misurano 8 m. Quanto misura il perimetro
dell’orto?
• Un pentagono ha i lati le cui misure sono
PROBLEMA
numeri interi consecutivi. Il perimetro misura
STRATEGICO 45cm. Calcola le misure dei lati.
• Disegna due rette che non sono né
perpendicolari né parallele
ESERCIZIO

9. La valutazione
• Prova carta-matita SPM (Lucangeli,
Tressoldi, Cendron 1998)
• Software SPM (Lucangeli, Tressoldi,
Cendron, Bertolo, Potenza, Stocchi)

10. La valutazione
10

11. PROCEDURA
1. Leggere attentamente il problema
2. Non eseguire operazioni prima di aver
svolto i passaggi preliminari
3. Segnare la risposta corretta per
ciascuna componente
4. Risolvere il problema
5. Autovalutare la corretta esecuzione

12. La valutazione

13. Gli strumenti specifici
Dalla classe seconda primaria alla
terza secondaria di primo grado
Conoscenze geometriche
Problemi di geometria
Abilità visuospaziali

14. Geometria test
Conoscenze
Problemi di geometria
geometriche

15. Geometria test
Abilità visuospaziali

16. Il potenziamento
Programmi di
potenziamento:
Risolvere i problemi in 6
mosse (De Candia, Cibinel,
Lucangeli 2009)
Risolvere problemi aritmetici
(Passolunghi, Bizzaro)
Problemi per immagini
(Bortolato)
16

17. Per approfondire:
• Cornoldi C. (2007). Difficoltà e Disturbi dell’Apprendimento.
Bologna: il Mulino
• D. Lucangeli, e M.C. Passolunghi (2001). Psicopatologia del calcolo e
della soluzione dei problemi. Trento: Erickson.
• Lucangeli, e Passolunghi (1995). Psicologia dell'apprendimento
matematico. Torino, Utet.
• Biancardi, Mariani, Pieretti (2003). La discalculia evolutiva. Dai
modelli neuropsicologici alla riabilitazione Franco Angeli
• www.airipa.it

18. daniela.lucangeli@unipd.it