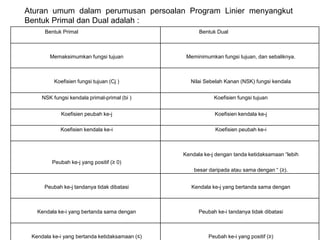
Dokumen tersebut membahas tentang program linier dan metode simpleks untuk menyelesaikan masalah program linier. Program linier digunakan untuk mengalokasikan sumber daya terbatas guna memaksimalkan keuntungan atau meminimalkan biaya. Metode simpleks adalah metode yang efisien untuk menyelesaikan masalah program linier dengan variabel keputusan lebih dari dua."

1. PENELITIA IOERASIONAL
TAMBANG
Disampaikan Oleh :
Admizal Nazki
Teknik Pertambangan
Jurusan Pertambangan
Universitas Negeri Padang
2016

2. PROGRAM LINEAR
Program linier merupakan metode matematik dalam mengalokasikan sumber daya
yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan
meminimumkan biaya. Program Linier banyak diterapkan dalam masalah ekonomi, industri,
militer, sosial dan lain-lain. Konsep dasar program linier telah ada pada jenjang pendidikan
dasar, yang dimulai pengenalan lambang bilangan yang direpresentasikan melalui gambar
benda di sekitar siswa, kemudian penjumlahan, pengurangan, perkalian serta
membandingkan banyaknya benda. Di Sekolah Menengah Pertama (SMP) konsep
diperluas melalui pembelajaran materi Sistem Persamaan Linier Satu Variabel (SPLSV),
kemudian ditingkatkan melalui materi Sistem Persamaan Linier Dua Variabel (SPLDV), di
Sekolah Menengah Atas (SMA) telah diperkenalkan sistem pertidaksamaan linier dan
materi khusus program linier yang menyajikan persoalan sehari-hari, kemudian
menerjemahkan permasalahan ke dalam model matematika, menyelesaikan sistem
pertidaksamaan yang merupakan kendala atau pembatas, mencari penyelesaian optimum,
menjawab permasalahan. Metode yang digunakan adalah metode grafik dengan
menggunakan uji titiksudut dan garis selidik. Pada tingkat universitas, terdapat mata kuliah
khusus program linier yang membahas metode penyelesaian program linier yang tujuannya
mencari keuntungan maksimum dan mengeluarkan biaya minimum. Metode yang diberikan
pada universitas adalah metode grafik, metode simpleks, metode analisis dual, metode
transportasi.

3. A. PROGRAM LINIER
Pemrograman Linier disingkat PL merupakan metode matematik dalam
mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan
seperti memaksimumkan keuntungan dan meminimumkan biaya. PL banyak
diterapkan dalam masalah ekonomi, industri, militer, sosial dan lain-lain. PL
berkaitan dengan penjelasan suatu kasus dalam dunia nyata sebagai suatu
model matematik yang terdiri dari sebuah fungsi tujuan linier dengan beberapa
kendala linier.
a. Formulasi Permasalahan
Urutan pertama dalam penyelesaian adalah mempelajari sistem relevan dan
mengembangkan pernyataan permasalahan yang dipertimbangakan dengan
jelas. Penggambaran sistem dalam pernyataan ini termasuk pernyataan tujuan,
sumber daya yang membatasi, alternatif keputusan yang mungkin (kegiatan atau
aktivitas), batasan waktu pengambilan keputusan, hubungan antara bagian yang
dipelajari dan bagian lain dalam perusahaan, dan lain-lain.
Penetapan tujuan yang tepat merupakan aspek yang sangat penting dalam
formulasi masalah. Untuk membentuk tujuan optimalisasi, diperlukan identifikasi
anggota manajemen yang benar-benar akan melakukan pengambilan keputusan
dan mendiskusikan pemikiran mereka tentang tujuan yang ingin dicapai.

4. LANJUTAN
b. Pembentukan model matematik
Tahap berikutnya yang harus dilakukan setelah memahami permasalahan
optimasi adalah membuat model yang sesuai untuk analisis. Pendekatan
konvensional riset operasional untuk pemodelan adalah membangun model
matematik yang menggambarkan inti permasalahan. Kasus dari bentuk cerita
diterjemahkan ke model matematik. Model matematik merupakan representasi
kuantitatif tujuan dan sumber daya yang membatasi sebagai fungsi variabel
keputusan. Model matematika permasalahan optimal terdiri dari dua bagian.
Bagian pertama memodelkan tujuan optimasi. Model matematik tujuan selalu
menggunakan bentuk persamaan. Bentuk persamaan digunakan karena kita
ingin mendapatkan solusi optimum pada satu titik. Fungsi tujuan yang akan
dioptimalkan hanya satu. Bukan berarti bahwa permasalahan optimasi hanya
dihadapkan pada satu tujuan. Tujuan dari suatu usaha bisa lebih dari satu.
Tetapi pada bagian ini kita hanya akan tertarik dengan permasalahan optimal
dengan satu tujuan.

5. lannjutan
Bagian kedua merupakan model matematik yang merepresentasikan
sumber daya yang membatasi. Fungsi pembatas bisa berbentuk persamaan
(=) atau pertidaksamaan (≤ atau ≥). Fungsi pembatas disebut juga sebagai
konstrain. Konstanta (baik sebagai koefisien maupun nilai kanan) dalam fungsi
pembatas maupun pada tujuan dikatakan sebagai parameter model. Model
matematika mempunyai beberapa keuntungan dibandingakan pendeskripsian
permasalahan secara verbal. Salah satu keuntungan yang paling jelas adala
model matematik menggambarkan permasalahan secara lebih ringkas. Hal ini
cenderung membuat struktur keseluruhan permasalahan lebih mudah
dipahami, dan membantu mengungkapkan relasi sebab akibat penting. Model
matematik juga memfasilitasi yang berhubungan dengan permasalahan dan
keseluruhannya dan mempertimbangkan semua keterhubungannya secara
simultan. Terakhir, model matematik membentuk jembatan ke penggunaan
teknik matematik dan komputer kemampuan tinggi untuk menganalisis
permasalahan

6. LANJUTAN
Di sisi lain, model matematik mempunyai kelemahan. Tidak semua
karakteristik sistem dapat dengan mudah dimodelkan menggunakan fungsi
matematik. Meskipun dapat dimodelkan dengan fungsi matematik, kadang-
kadang penyelesaiannya sulit diperoleh karena kompleksitas fungsi dan teknik
yang dibutuhkan.
Bentuk umum pemrograman linier adalah sebagai berikut :
Fungsi tujuan :
Maksimumkan atau minimumkan z = c1x1 + c2x2 + ... + cnxn
Sumber daya yang membatasi :
a11x1 + a12x2 + ... + a1nxn = /≤ / ≥ b1
a21x1 + a22x2 + … + a2nxn = /≤ / ≥ b2
…
am1x1 + am2x2 + … + amnxn = /≤ / ≥ bm
x1, x2, …, xn ≥ 0

7. LANJUTAN
Simbol x1, x2, ..., xn (xi) menunjukkan variabel keputusan. Jumlah variabel
keputusan (xi) oleh karenanya tergantung dari jumlah kegiatan atau aktivitas
yang dilakukan untuk mencapai tujuan. Simbol c1,c2,...,cn merupakan kontribusi
masing-masing variabel keputusan terhadap tujuan, disebut juga koefisien
fungsi tujuan pada model matematiknya.Simbol a11, ...,a1n,...,amn merupakan
penggunaan per unit variabel keputusan akan sumber daya yang membatasi,
atau disebut juga sebagai koefisien fungsi kendala pada model matematiknya.
Simbol b1,b2,...,bm menunjukkan jumlah masing-masing sumber daya yang ada.
Jumlah fungsi kendala akan tergantung dari banyaknya sumber daya yang
terbatas.
Pertidaksamaan terakhir (x1, x2, …, xn ≥ 0) menunjukkan batasan non
negatif. Membuat model matematik dari suatu permasalahan bukan hanya
menuntut kemampuan matematik tapi juga menuntut seni permodelan.
Menggunakan seni akan membuat permodelan lebih mudah dan menarik.

8. Kasus pemrograman linier sangat beragam. Dalam setiap
kasus, hal yang penting adalah memahami setiap kasus
dan memahami konsep permodelannya. Meskipun fungsi
tujuan misalnya hanya mempunyai kemungkinan bentuk
maksimisasi atau minimisasi, keputusan untuk memilih
salah satunya bukan pekerjaan mudah. Tujuan pada suatu
kasus bisa menjadi batasan pada kasus yang lain. Harus
hati-hati dalam menentukan tujuan, koefisien fungsi tujuan,
batasan dan koefisien pada fungsi pembatas

9. B. METODE SIMPLEKS
Pada bagian terdahulu masalah program linear dengan dua peubah
keputusan masih dapat diselesaikan dengan metode grafik. Akan tetapi
pada kenyataannya masalah program linear yang dihadapi kebanyakan
lebih dari dua peubah keputusan dengan berbagai macam batasan,
sehngga dipandang tidak efisien bila menggunakan metode grafik untuk
mencari penyelesaian optimumnya.
Menghadapi masalah program linear yang memiliki peubah keputusan lebih
dari dua, metode simpleks yang lebih efisien. Metode simpleks merupakan
pengembangan metode aljabar yang hanya menguji sebagaian dari jumlah
penyelesaian yang layak dalam bantuan tabel. Penggunaan dalam bentuk
tabel ini membuat metode simpleks lebih siap untuk digunakan dengan
bantuan komputer.

10. lanjutan
a. Bentuk-Bentuk Masalah Program Linear
Kendala utama masalah program linear dapat berbentuk ≤ atau = , I =
1,2,3,4,… m (ada m banyaknya kendala, k peubah keputusan) kendala yang
berbentuk pertidaksamaan dapat diubah menjadi persamaan beberapa cara
sebagai berikut:
(i) Bentuk kendala xj ≤ bi. dapat diubah dengan menyisipkan peubah
tambahan st pada ruas kiri sedimikian hingga + st = bt dengan st ≥ 0.
Dalam hal ini, st = 0, bila = bi dan sj > 0 bila <>I
(ii) <>i, dapat diubah dengan menyisipkan peubah tambahan c1 pada ruas
kanan sedemikian sehingga = + ti atau i, dengan bi ≥ 0
Sesuai dengan fungsinya, s1 disebut peubah kekurangan (slack variabel) dan
t1 disebut peubah kelebihan (surplus variabel).

11. LANJUTAN
Berdasarkan perubahan di atas, himpunan kendala utama akan berubah
menjadi susunan persamaan linear.
= bi, i = 1, …, m
ialah dengan memberi lambang peubah-peubah kekurangan atau kelebihan
dengan xj dimulai dari j = k + 1 samapi j = n. supaya penyelesaian susunan ini
menjadi layak masih harus dipenuhi kendala tidak negative
Xj ≥ 0, j = 1, …, n
Pada umumnya susunan persamaan linear (1) di atas termasuk jenis
yang mempunyai peyelesaian tidak terhingga banyaknya. Di antara
peyelesaian (1) dicari yang juga memenuhi kendala tidak negative (2), dan
inipun pada umumnya masih tidak terhingga banyaknya. Kemudian, diantara
penyelesaian layak yang tidak terhingga banyaknya ini, kita mencari yang
mengoptimumkan fungsi tujuan, utnuk memperoleh penyelesaian yang
optimum

12. lanjutan
Untuk menyesuaikan dengan bentuyk kendala yang baru, fungsi tujuan yang
semula berbentuk
Z = dilengkapi menjadi
Z = dengan ck+1 = ck+2 = ck+3 …= cn = 0
Oleh karena itu, masalah program linear dapat digambarkan dalam
berbagai bentuk seperti maksimasi atau minimasi dan dengan kendala dapat
pula berbentuk lebih kecil atau sama dengan, sama dengan, atau lebih besar
atau sama dengan (≤, =, ≥), maka diperlukan suatu bentuk baku yang dapat
memenuhi prosedur penyelesaian yang optimum. Bentuk baku yang sudah
umum digunakan untuk meyelesaikan model program linear dapat
dikemukakan sebagai berikut

13. LANJUTAN
1. bentuk baku
bentuk baku dari masalah program linear dengan m kendala dan n
peubah, merupakan bentuk umum program linear. Keutamaan dari bentuk
baku ini adalah: (a) fungsi tujuan berbentuk maksimum atau minimum, (b)
semua kendala utama digambarkan dalam bentuk persamaan, (c) semua
peubah keputusan tidak negative, dan (d) nilai ruas kanan setiap kendala tidak
negative . dalam bentuk baku maslah program linear dapat digambarkan
bentuk soal sebagai berikut :
mencari xj, j = 1, …, n
yang memenuhi = bi I = 1, …, m
atau memaksimumkan atau meminimumkan
Z =
Apabila fungsi tujuan diamaksimumkan maka soal disebut berpola maksimum ,
dan bila fungsi tujuan diminimumkan maka soal disebut berpola minimum.

14. LANJUTAN
2. bentuk kanonik
bentuk kanonik mempunyai karakteristik sebagai berikut: (a) fungsi tujuan
berbentuk maksimasi atau minimasi, (b) semua kendala utama berbentuk lebih
kecil atau sama dengan (≤) untuk fungsi tujuan maksimum atau semua kendala
utama berbentuk lebih besar atau sama dengan (≥) untuk fungsi tujuan minimum,
(c)semua peubah keputusan tidak negative. Dalam bentuk kanonik masalah
program linear dapat digambarkan bentuk soal sebagai berikut:
mencari xj, j = 1,2 …n
yang memenuhi , I = 1, … , m
x1 ≥ 0
untuk maksimumkan Z =
hubungan dalam semua kendala utama berbentuk disebut berbentuk kanonik
maksimum
mencari xj, j = 1,2 …n
yang memenuhi , i = 1, … , m
x1 ≥ 0
untuk maksimumkan Z =
hubungan dalam semua kendala utama berbentuk ≥ disebut berbentuk kanonik
minimum

15. Contoh SOAL
Tulis bentuk baku dari soal yang berbunyi:
Mencari x,y yang memenuhi
5x + 4y ≤ 200
3x + 6y = 180
8x + 5y ≥ 160
x, y ≥ 0 kendala tidak negative
untuk meminimumkan Z = 4x + 5y
penyelesaian:
sisipkan peubah s pada kendala pertama dan peubah t pada kendala ketiga
sehingga soal menjadi:
mencari x, y, s, t yang memenuhi
5x + 4y + s = 200
3x + 6y = 180
8x + 5y - t = 160
x, y, s, t ≥ 0 kendala tidak negative
untuk meminimumkan Z = 4x + 5y + 0s + 0t
soal ini sudah berbentuk baku dengan x,y peubah asli, s peubah kekurangan
dan t peubah kelebihan

16. b. Tahapan-Tahapan Penyelesaian
Metode Simpleks
1. Tahap pra analisis
i. mengenali masalah PL yang diajukan:
beberapa keterangan yang perlu diajukan pada tahap ini, yaitu apakah fungsi
tujuan
· meminimumkan atau memaksimumkan?
· Terdapat berapa banyak peubah asli?
· Terdapat berapa banyakkendala utama?
ii. Konversi semua kendala kedalam bentuk baku (system persamaan)
· Masukkan peubah kekurangan (slack) atau,
· Masukkan peubah kelebihan (surplus) atau,
· Masukkan peubah semu (artifisial)

17. 2. Tahap analisis
i Tentukan pemecahan layak dasar (basis) awal
ii Sajikan data masalah PL ke dalam tabel simpleks awal
iii Tentuka kolom peubah yang akan masuk dalam dasar, kolom ini disebut kolom
kunci. Apabila masalah PL berpola maksimum keuntungan, maka penentuan
kolom kunci ini ditandai oleh nilai pada baris zj – cj yang memepunyai nilai
negative terbesar (zj – cj ¸0). Dan apabila berpola minimum biaya, maka kolom
kunci ditandai oleh nilai pada baris zj – cj yang mempunyai nilai positif terbesar
(zj – cj > 0)
iv Tentukan peubah yang akan keluar dasar (disebut baris kunci) dengan Ri yang
terkecil.
v Cari unsur baru yang terdapat pada baris kunci dengan cara membagi semua
unsur yang terdapat pada baris kunci dengan unsur kunci. Unsur kunci adalah
unsur yang terdapat pada persilangan pada baris kunci dengan kolom kunci.
vi Mencari unsure baru pada baris yang laindengan aturan unsure pada baris
baru = unsur pada baris lama dikurangi dengan hasil kali unsure pada kolom
kunci dengan unsur baru baris kunci.
vii Apabila penyelesaian optimum belum trcapai pada tabel yang bersangkutan,
maka ulangi kembali langkah (iii) sampai dengan ditemukannya penyelsaian
optimum. Penyelesaian optimum tercapai bila zj – cj ≤ 0 untuk semua j pada pola
minimum.

18. lanjutan
Maks/Min Ci
CB XB X1 X2 …. xn bn R1
CB1
CB2
.
.
.
CBM
XB1
XB2
.
.
.
XBM
a11
a21
.
.
.
am1
a12
a22
.
.
.
am2
….
….
….
….
….
….
a1n
a2n
.
.
.
amn
b1
b2
.
.
.
bm
R1
R2
.
.
.
Rm
zj Z1 Z2 …. zmn z
zj - cj Z1-c1 Z2-c2 … Zn-cn
Untuk mengoperasikan data-data soal dan menerapkan tahapan-tahapan di
atas disusun tabel yang kemudian disebut tabel simpleks sebagai berikut
Tabel simpleks

19. Keterangan tabel :
CJ : koefisien ongkos dari fungsi tujuan dan koefisien peubah kekurangan/
kelebihan/ semu
CB : Koefisien ongkos untuk peubah dasar XB
XB : Peubah yang menjadi dasar dalam tabel yang ditinjau
Xj : Peubah-peubah lengkap (asli/kekurangan/kelebihan/semu)
aij : koefisien teknis
bi : suku tetap (tidak negatif) atau nilai ruas kanan setiap kendala
zj : (hasil kali dari CB dengan kolom aij )
z : (hasil kali dari CB dengan bi
zj - cj : selisih zj dengan cj
Apabila tabel bersangkutan belum optimal dan Xb terpilih sebagai dasar baru
maka dibuat kolom Ri yang diperoleh dengan Ri = , hanya untuk aek > 0.

20. c. Pemecahan awal yang layak
Penyelesaian masalh program linear dengan metode simpleks,
menghendaki adanya pemecahan awal yang layak pada awal
perhitungan.tanpa adanya pemecahan awal yang layak (dasar awal yang
layak), maka tabel simpleks tidak dapat dibentuk. Hal demikian tentu saja tidak
dapat ditemui pad setiap permasalahn program linear. Untuk dapat
menyelesaikan permasalahn program linear sehingga didapat pemecahan
awal yang layak. Pendekatan dasar yangdapat ditempuh adalah dengan
penambahan peubah semu (artificial variabel).

21. Contoh
Tentukan x1 dan x2 tidak negative dan maksimumkan X = 4x1+5x2 yang
memenuhi
5x1 + 4x2 ≤ 200
3x1 + 6x2 = 180
8x1 + 5x2 ≥ 160
X1, x2 ≥ 0
Soal diatas diuba ke bentuk baku dengan menyisipkan peubah kekurangan
ke dalam kendala ke-1 dan peubah kelebihan ke dalam kendala ke-3, sedang
kendala ke-2 tidak memerlukan karena sudah berbentuk persamaan, jadi aoal
sekarang adalah
Tentukan x1, x2, x3, x4 tidak negative dan
Maksimumkan Z = 4x1 + 5x2 + 0x3 + 0x4
5x1+ 4x2 + x3 = 200
3x1 + 6x2 = 180
8x1 + 5x2 - x4 = 160 dan
x1, x2, x3, x4 ≥ 0

22. LANJUTAN
sekarang dipeiksa apakah semua kendala utama tersebut memliki peubah
dasar yang layak?
· Kendala ke-1 : memiliki peubah dasar yang layak yaitu x3
· Kendala ke-2 : belum memiliki peubah dasar
· Kendala ke-3 : memiliki peubah dasar tapi tidak layak, karena memuat
nilai negative untuk -x4
Oleh karena itu, tabel awal simpleks belum dapat dibuat. Untuk
mendapatkan pemecahan awal yang layak, maka kendala ke-2 dan ke-3 perlu
ditambahkan peubah semu yang bertindak sebagi peubah dasar yang layak.
Sebagai akibat, timbul syarat perlu supaya soal asli mempunyai
penyelesaian optimum ialah bahwa dalam tabel optimum peubah semu harus
bernilai nol.

23. lanjutan
Dengan demikian diharapkan bahwa peubah semu segera keluar dari dasar
karena koefisien ongkosnya negative besar, sehingga soal menjadi :
Tentukan x1, x2, x3, x4 tidak negative dan
Maksimumkan Z = 4x1 + 5x2 + 0x3 + 0x4 – Mx5 – Mx6
5x1+ 4x2 + x3 = 200
3x1 + 6x2 -x5 = 180
8x1 + 5x2 - x4 -x6 = 160 dan
x1, x2, x3, x4 , x5, x6 ≥ 0
sekarang soal sudah siap untuk dimasukan ke dalam tabel simpleks awal

24. C. ANALISIS PRIMAL - DUAL
Setiap persoalan program linier selalu mempunyai dua macam analisis,
yaitu : analisis primal dan analisis dual yang biasanya disebut analisis
primal-dual.
Model Umum Persoalan Primal – Dual
Bentuk Primal :
Maksimumkan :
syarat ikatan : ≤ bi untuk i= 1, 2, 3, ...,m.
dan Xj ≥ 0, j = 1, 2, ... , n
Kalau akan dinyatakan menjadi Bentuk Dual :
Minimumkan : F =
syarat ikatan : ≥ Cj , untuk j= 1, 2, 3, ...,n.
Yi ≥ 0, I = 1,2,… m
Dimana: Zopt = adalah sama dengan Fopt =

25. Aturan umum dalam perumusan persoalan Program Linier menyangkut
Bentuk Primal dan Dual adalah :
Bentuk Primal Bentuk Dual
Memaksimumkan fungsi tujuan Meminimumkan fungsi tujuan, dan sebaliknya.
Koefisien fungsi tujuan (Cj ) Nilai Sebelah Kanan (NSK) fungsi kendala
NSK fungsi kendala primal-primal (bi ) Koefisien fungsi tujuan
Koefisien peubah ke-j Koefisien kendala ke-j
Koefisien kendala ke-i Koefisien peubah ke-i
Peubah ke-j yang positif (≥ 0)
Kendala ke-j dengan tanda ketidaksamaan “lebih
besar daripada atau sama dengan “ (≥).
Peubah ke-j tandanya tidak dibatasi Kendala ke-j yang bertanda sama dengan
Kendala ke-i yang bertanda sama dengan Peubah ke-i tandanya tidak dibatasi
Kendala ke-i yang bertanda ketidaksamaan (≤) Peubah ke-i yang positif (≥)

26. D. METODE TRANSPORTASI
Metode Transportasi merupakan suatu metode yang digunakan untuk
mengatur distribusi dari sumber-sumber yang menyediakan produk yang sama
ke tempat-tempat yang membutuhkan secara optimal dengan biaya yang
termurah . Alokasi produk ini harus diatur sedemikian rupa karena terdapat
perbedaan biaya-biaya alokasi dari satu sumber atau beberapa sumber ke
tempat tujuan yang berbeda.
Tabel awal dapat dibuat dengan dua metode, yaitu:
1. Metode North West Corner (NWC) => dari pojok kiri atas ke pojok kanan
bawah
Kelemahan : tidak memperhitungkan besarnya biaya sehingga kurang
efisien.
2. Metode biaya terkecil => mencari dan memenuhi yang biayanya terkecil
dulu. Lebih efisien dibanding metode NWC.
Setelah tabel awal dibuat, tabel dapat dioptimalkan lagi dengan metode:
1. Stepping Stone (batu loncatan)
2. Modified Distribution Method (MODI)
Selain metode-metode di atas masih ada satu metode yang lebih sederhana
penggunaannya yaitu metode Vogel’s Approximation Method (VAM).