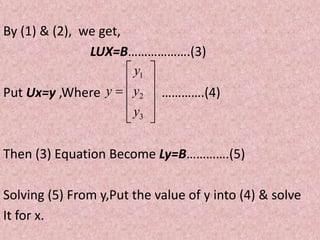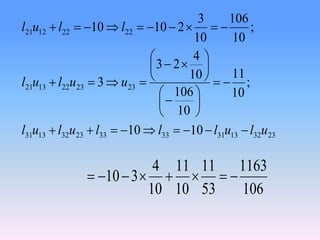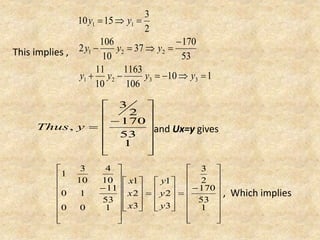The document discusses LU decomposition, a method to solve simultaneous linear equations. It can be summarized as: 1. LU decomposition involves factoring a matrix A into the product of a lower triangular matrix L and upper triangular matrix U. 2. This allows transforming the system of equations Ax=b into Ly=b and Ux=y, which can then be solved step-by-step. 3. As an example, a 3x3 system is factorized and the solutions for x, y are obtained and back substituted to find the final solutions.

1. SUBJECT TEACHER:- GROUP STUDENTS:-
 Dr.Leena Rani  Madhav Pandey
 Mayank Kumar

3. LU Decomposition
 LU Decomposition is
another method to solve a set of
simultaneous linear equations.
z

4. [A] = [L][U]
where
[L] = lower triangular matrix
[U] = upper triangular matrix
Let A be a n × n square matrix. The LU decomposition is the
technique of factoring a matrix A as a product of Lower
triangular matrix (L) and upper triangular matrix (U). That
is, A=LU where L and U have same dimension of A.

5.     





















33
2322
131211
3231
21
00
0
1
01
001
u
uu
uuu
ll
lULA
•Consider the system of equation
AX=B…………………(1)
Let A=LU…………(2)
Where

6. By (1) & (2), we get,
LUX=B……………….(3)
Put Ux=y ,Where ………….(4)
Then (3) Equation Become Ly=B………….(5)
Solving (5) From y,Put the value of y into (4) & solve
It for x.











3
2
1
y
y
y
y

7. 101023
373102
154310
321
321
321



xxx
xxx
xxx


































10
37
15
1023
3102
4310
3
2
1
x
x
x
In marix form, the given system of equation can be
written as ,

8. Which is of the form Ax=b. Let A=LU, Which implies

































33
2322
131211
3231
21
00
0
1
01
001
1023
3102
4310
u
uu
uuu
ll
l












332332133132123131
2322132122122121
1311121111
lulullull
ulullull
ulull
;
10
4
;
10
3
;3,2,10 1312312111  uulll

9. 23321331333323321331
2323221321
22221221
1010
;
10
11
10
106
10
4
23
3
;
10
106
10
3
21010
ululllulul
uulul
llul


















106
1163
53
11
10
11
10
4
310 

10. Therefore,we get,
Now,Let Ux=y,then Ly=b implies





































100
53
11
10
10
4
10
3
1
106
1163
10
11
3
0
10
106
2
0010
andUl








































10
37
15
3
2
1
106
1163
10
11
3
0
10
106
2
0010
y
y
y

11. This implies ,
and Ux=y gives
, Which implies
110
106
1163
10
11
53
170
37
10
106
2
2
3
1510
3321
221
11




yyyy
yyy
yy
















1
53
170
2
3
, yThus
























































1
53
170
2
3
3
2
1
3
2
1
100
53
11
10
10
4
10
3
1
y
y
y
x
x
x

12. By back substitution,we get
Therefore, the required solution by LU decompostion method
(Crout’s method)is
1
53
170
53
11
2
3
10
4
10
3
3
32
321




x
xx
xxx
21
10
4
)3(
10
3
2
3
10
4
10
3
2
3
3
53
170
53
111
1
321
2
3





xxx
x
x
.1,3,2 321  xxx