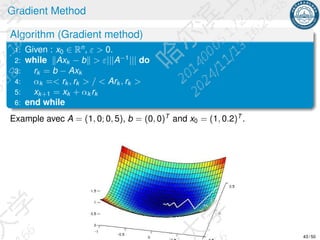
The document discusses numerical methods for solving linear systems of equations, focusing on direct and iterative methods, with computational costs generally being O(n^3). It covers techniques such as LU decomposition, both with and without pivoting, and introduces Cholesky decomposition for positive definite matrices. The document emphasizes efficiency and stability in solving systems while providing examples and algorithms for practical application.

1. Resolution of Linear System
Chang YANG
School of Mathematics, Harbin Institute of Technology, Harbin, China
Autumn, Semester
1 / 50

2. This chapter introduce different numerical methods for solving linear system
Ax = b.
Motivations
In generally, the resolution of linear system is almost the most costly part of a
numerical algorithm. How to solve linear system efficiently?
Two types of methods:
(i)
Direct methods: Factorization of the matrix A and solve exactly the linear
system.
(ii)
Iterative methods: Solve the linear system approximately.
Computational cost:
In general case, the computational cost is O(n3
), where n is the size of the
matrix.
2 / 50

3. Simple Examples
Diagonal matrix



a1,1 0
...
0 an,n






x1
.
.
.
xn


 =



b1
.
.
.
bn


 =⇒



x1 = b1/a1,1,
xi = bi /ai,i ,
xn = bn/an,n.
Computational cost -> O(n).
Triangle matrix





a1,1 a1,2 . . . a1,n
a2,2 . . . a2,n
...
.
.
.
0 an,n










x1
x2
.
.
.
xn





=





b1
b2
.
.
.
bn





=⇒





xn = bn/an,n,
xn−1 =
bn−1−an−1,nxn
an−1,n−1
,
xk =
bk −
Pn
j=k+1 ak,j xj
ak,k
.
Computational cost -> O(n2
).
3 / 50

4. Outline
1 Direct Methods
2 Condition Number and Error for Resolution of Linear Systems
3 Classical Iterative Methods
4 / 50

5. Table of contents
1 Direct Methods
2 Condition Number and Error for Resolution of Linear Systems
3 Classical Iterative Methods
5 / 50

6. LU decomposition: General idea
The LU decomposition consists to factorize A as follows
PA = LU,
with
L =





1 0
l2,1 1
.
.
.
...
ln,1 . . . ln,n−1 1





and U =





u1,1 u1,2 . . . u1,n
u2,2 . . . u2,n
...
.
.
.
0 un,n





and P is a permutation matrix (P−1
= PT
).
Motivation: The resolution of linear system is made by two steps
LUx = Pb =⇒
Ly = Pb,
Ux = y.
6 / 50

7. LU decomposition without pivot
Hypothesis :
Assume all the principle matrices of A are invertible, i.e. det(Ak ) ̸= 0, with
Ak =



a1,1 . . . a1,k
.
.
.
.
.
.
ak,1 . . . ak,k


 , ∀k = 1, . . . , n.
Then there exists a decomposition LU with P = Id, i.e.
A = LU.
Example in dimension 3:
A =


a1,1 a1,2 a1,3
a2,1 a2,2 a2,3
a3,1 a3,2 a3,3

 , and
a1,1 = det(A1) ̸= 0,
a1,1a2,2 − a2,1a1,2 = det(A2) ̸= 0.
7 / 50

8. LU decomposition without pivot
With
G1 =


1 0 0
−q2,1 1 0
−q3,1 0 1

 , with
(
q2,1 =
a2,1
a1,1
,
q3,1 =
a3,1
a1,1
.
We have
A(1)
= G1A =



a1,1 a1,2 a1,3
0 a
(1)
2,2 a
(1)
2,3
0 a
(1)
3,2 a
(1)
3,3


 , with











a
(1)
2,2 = a2,2 − a1,2q2,1,
a
(1)
2,3 = a2,3 − a1,3q2,1,
a
(1)
3,2 = a3,2 − a1,2q3,1,
a
(1)
2,3 = a3,3 − a1,3q3,1.
We restart with A(1)
:
G2 =


1 0 0
0 1 0
0 −q3,2 1

 , with q3,2 =
a
(1)
3,2
a
(1)
2,2
.
8 / 50

9. LU decomposition without pivot
A(2)
= G2G1A =



a1,1 a1,2 a1,3
0 a
(1)
2,2 a
(1)
2,3
0 0 a
(2)
3,3


 , with a
(2)
3,3 = a
(1)
3,3 − a
(1)
1,3q3,2.
Finally,
A = (G2G1)−1



a1,1 a1,2 a1,3
0 a
(1)
2,2 a
(1)
2,3
0 0 a
(2)
3,3


 = LU,
where L = (G2G1)−1
= G−1
1 G−1
2 , i.e.
L =


1 0 0
q2,1 1 0
q3,1 0 1




1 0 0
0 1 0
0 q3,2 1

 =


1 0 0
q2,1 1 0
q3,1 q3,2 1

 .
9 / 50

10. LU decomposition without pivot
Algorithm: LU decomposition without pivot
for k = 1 : n − 1 do
for i = k + 1 : n do
qi,k = a
(k−1)
i,k /a
(k−1)
k,k
for j = k + 1 : n do
a
(k)
i,j = a
(k−1)
i,j − qi,k a
(k−1)
k,j
end for
end for
end for
Exercise
Compute the computational cost this algorithm.
10 / 50

11. LU decomposition without pivot
Example with
A =


1 4 7
2 5 8
3 6 11

 , and b =


18
24
32

 .
We compute q2,1 = a2,1/a1,1 = 2, q3,1 = a3,1/a1,1 = 3.


1 4 7 18
2 5 8 24
3 6 11 32

 =⇒


1 4 7 18
0 −3 −6 −12
0 −6 −10 −22

 .
Then we compute q3,2 = a
(1)
3,2/a
(1)
2,2 = 2.


1 4 7 18
0 −3 −6 −12
0 −6 −10 −22

 =⇒


1 4 7 18
0 −3 −6 −12
0 0 2 2

 .
11 / 50

12. LU decomposition without pivot
Finally,
A =


1 4 7
2 5 8
3 6 11

 =


1 0 0
2 1 0
3 2 1




1 4 7
0 −3 −6
0 0 2

 .
The resolution of linear system is performed by two steps:


1 0 0
2 1 0
3 2 1




y1
y2
y3

 =


18
24
32

 =⇒


y1
y2
y3

 =


18
−12
2

 ,


1 4 7
0 −3 −6
0 0 2




x1
x2
x3

 =


18
−12
2

 =⇒


x1
x2
x3

 =


3
2
1

 .
12 / 50

13. LU decomposition with pivot
Motivation
The LU decomposition is unstable when the coefficients a
(i)
i+1,i+1 is too small,
or the principle matrices are no longer invertible.
In practice, it is more efficient to use a LU decomposition with pivot.
Example with
A =


0 2 2
4 2 4
2 4 4

 , and b =


4
10
10

 .
We start by choosing the pivot, the largest element of the first column, then
we proceed the same LU algorithm without pivot.


0 2 2 4
4 2 4 10
2 4 4 10

 =⇒ P1 =


0 1 0
1 0 0
0 0 1

 =⇒


4 2 4 10
0 2 2 4
2 4 4 10

 ,


4 2 4 10
0 2 2 4
0 3 2 5

 =⇒ P2 =


1 0 0
0 0 1
0 1 0

 =⇒


4 2 4 10
0 3 2 5
0 2 2 4

 ,
13 / 50

14. LU decomposition with pivot


4 2 4 10
0 3 2 5
0 2 2 4

 =⇒


4 2 4 10
0 3 2 5
0 0 2/3 2/3

 .
Therefore, 


x3 = 1,
x2 = (5 − 2)/3 = 1,
x1 = (10 − 4 − 2)/4 = 1,
and
P = P2P1 =


1 0 0
0 0 1
0 1 0




0 1 0
1 0 0
0 0 1

 =


0 1 0
0 0 1
1 0 0

 ,
L =


1 0 0
1/2 1 0
0 2/3 1

 U =


4 2 4
0 3 2
0 0 2/3

 .
14 / 50

15. LU decomposition with pivot
The previous calculation yields
G2P2G1P1A = U.
By denoting M = G2P2G1P1, we have
MA = U,
MP−1
PA = U,
where P = P2P1. This implies
PA = (PM−1
)U.
Finally, L = PM−1
= P2P1P−1
1 G−1
1 P−1
2 G−1
2 = P2G−1
1 P−1
2 G−1
2 .
Exercise
Solve the linear system by using the LU decomposition with pivot
A =


3 1 6
2 1 3
1 1 1

 , and b =


2
4
7

 .
15 / 50

16. Cholesky Decomposition
The Cholesky decomposition consists to decompose the matrix A under the
form A = LLT
, where
L =





l1,1 0
l2,1 l2,2
.
.
.
...
ln,1 . . . ln,n−1 ln,n





Motivation
As the LU decomposition, the resolution of linear system Ax = b is performed
by two steps:
LLT
x = b =⇒
Ly = b,
LT
x = y.
The advantages with respect to the LU decomposition are
1 only have to store one matrix;
2 twice faster than the LU decomposition.
16 / 50

17. Cholesky Decomposition
Definition
A matrix A is positive definite if
x, Ax ≥ 0 and x, Ax = 0 =⇒ x = 0.
An example of such matrix are the diagonal strictly dominant matrices.
Theorem
If A is a symmetric positive definite matrix, then there are a unique inferior
triangular matrix L with positive diagonal coefficients such that
A = LLT
.
17 / 50

18. Cholesky Decomposition
Example in dimension 2
Let A =
a c
c b
be a positive definite matrix.
In particular, the hypothesis of positivity implies that
a = e1, Ae1 0,
ab − c2
= det(A) 0.
With
L =
l1,1 0
l2,1 l2,2
and LLT
=
l2
1,1 l1,1l2,1
l2,1l1,1 l2
2,1 + l2
2,2
.
We thus reduce that 




l1,1 =
√
a,
l2,1 = c
√
a
,
l2,2 =
q
b − c2
a .
18 / 50

19. Cholesky Decomposition
In general case,




l1,1 0
l2,1 l2,2
.
.
.
...
ln,1 . . . ln,n−1 ln,n









l1,1 l2,1 . . . ln,1
l2,2
.
.
.
... ln,n−1
0 ln,n





=





a1,1 a1,2 . . . a1,n
a1,2 a2,2
.
.
.
.
.
.
... an−1,n
a1,n . . . an−1,n an,n





.
The first row implies that a1,i = l1,1li,1 and



l1,1 =
√
a1,1,
li,1 =
a1,i
l1,1
, for i 1.
Thus, the first column is obtained.
The second row implies that a2,i = l2,1li,1 + l2,2li,2, for i ≥ 2 and



l2,2 =
q
a2,2 − l2
2,1,
li,2 =
a2,i −l2,1li,1
l2,2
, for i 2.
Thus, the second column is obtained.
19 / 50

20. Cholesky Decomposition




l1,1 0
l2,1 l2,2
.
.
.
...
ln,1 . . . ln,n−1 ln,n









l1,1 l2,1 . . . ln,1
l2,2
.
.
.
... ln,n−1
0 ln,n





=





a1,1 a1,2 . . . a1,n
a1,2 a2,2
.
.
.
.
.
.
... an−1,n
a1,n . . . an−1,n an,n





.
At the kth row, the k − 1 first columns of L are known, then
ak,i =
k
X
j=1
lk,j li,j , for i ≥ k
and 




lk,k =
q
ak,k −
Pk−1
j=1 l2
k,j ,
li,k =
ak,i −
Pk−1
j=1
lk,j li,j
lk,k
, for i k.
Thus, the kth column of L is obtained.
20 / 50

21. Cholesky Decomposition
Algorithm: Cholesky Decomposition
for k = 1 : n − 1 do
lk,k =
q
ak,k −
Pk−1
j=1 l2
k,j
for i = k + 1 : n do
li,k =
ak,i −
Pk−1
j=1
lk,j li,j
lk,k
end for
end for
Exercise
Compute the computational cost this algorithm.
Exercise
Apply the algorithm of Cholesky to decompose the matrix
A =


4 2 1
2 4 2
1 2 4

 .
21 / 50

22. Table of contents
1 Direct Methods
2 Condition Number and Error for Resolution of Linear Systems
3 Classical Iterative Methods
22 / 50

23. The condition number of a matrix
Motivation
How an error δA of matrix A and an error δb of a vector b affect the solution x
of the linear system
Ax = b.
In particular, by denoting x + δx, the solution of linear system
(A + δA)(x + δx) = b + δb,
we expect to control the relative error
∥δx∥
∥x∥
.
23 / 50

24. Vectorial Norm
Definition
∥ · ∥ is a norm in Rn
verifying that if ∀(x, y) ∈ (Rn
)2
and α ∈ R, then
Positivity : ∥x∥ 0 and ∥x∥ = 0 ⇐⇒ x = 0.
Linearity : ∥αx∥ = |α|∥x∥.
Triangular Inequality : ∥x + y∥ ≤ ∥x∥ + ∥y∥.
Example :
∥x∥2 =
qPn
i=1 x2
i .
∥x∥1 =
Pn
i=1 |xi |.
∥x∥∞ = maxi=1:n{|xi |}.
24 / 50

25. Matrix Norm
Definition
Let ∥ · ∥ be a norm in Rn
. We denote ||| · ||| an associated norm of matrix
space Rn×n
defined by
|||A||| = max
∥x∥≤1
||Ax|| = max
∥x∥
||Ax||
∥x∥
.
Exercise
Prove that ||| · ||| is a norm in matrix space Rn×n
.
Example :
|||A|||2 =
√
λmax, where λmax is the largest eigenvalue of the matrix AT
A.
|||A|||1 = maxj=1:n
Pn
i=1 |ai,j |.
|||A|||∞ = maxi=1:n
Pn
j=1 |ai,j |.
25 / 50

26. Condition Number
Definition
Let A ∈ Rn×n
be an invertible matrix. The condition number associated with a
given norm is defined by
cond(A) = |||A||| · |||A−1
|||.
Exercise
Compute condition number associated to the norm ∥ · ∥∞ of the matrix
A =
1.2969 0.8648
0.2161 0.1441
.
26 / 50

27. Condition Number
Theorem
Let x and x + δx be the solution of the linear systems
Ax = b,
A(x + δx) = b + δb.
Then
∥δx∥
∥x∥
≤ cond(A)
∥δb∥
∥b∥
.
Proof :
It is sufficient to remark that
Ax = b =⇒ ∥b∥ ≤ |||A||| · ∥x∥ =⇒ 1
∥x∥ ≤ |||A|||
∥b∥ .
Aδx = δb =⇒ ∥δx∥ ≤ |||A−1
||| · ∥δb∥.
27 / 50

28. Condition Number
Theorem
Let x and x + δx be the solution of the linear systems
Ax = b,
(A + δA)(x + δx) = b + δb.
Assume that |||A−1
||| · |||δA||| 1. Then
∥δx∥
∥x∥
≤
cond(A)
1 − |||A||| · |||δA|||
∥δb∥
∥b∥
+
|||δA|||
|||A|||
.
Proof :
By introducing δx = δxb + δxA, where
Aδxb = δb,
it yields that
Ax = b =⇒ ∥b∥ ≤ |||A||| · ∥x∥ =⇒
1
∥x∥
≤
|||A|||
∥b∥
,
Aδxb = δb =⇒ ∥δxb∥ ≤ |||A−1
||| · ∥δb∥,
28 / 50

29. Condition Number
and
(A + δA)(x + δxb + δxA) = b + δb =⇒ δxA = −A−1
δA(x + δx)
=⇒ ∥δxA∥ ≤ |||A−1
||| · |||δA|||(∥x∥ + ∥δx∥).
We thus reduce that
∥δx∥ ≤ ∥δxA∥ + ∥δxb∥ ≤ |||A−1
||| · ∥δb∥ + |||A−1
||| · |||δA|||(∥x∥ + ∥δx∥),
and
∥δx∥ ≤
1
1 − |||A−1||| · |||δA|||
|||A−1
||| · ∥δb∥ + |||A−1
||| · |||δA|||∥x∥
.
29 / 50

30. Table of contents
1 Direct Methods
2 Condition Number and Error for Resolution of Linear Systems
3 Classical Iterative Methods
30 / 50

31. Classical Iterative Methods
Motivations :
The computational cost of the direct method is O(N3
).
Usually, the matrix A is sparse (which means the majority coefficients
are zeros). While the LU decomposition losses this property. Thus we
have to face the problem of storage.
Example:
31 / 50

32. Fixed point method
The principle is to search the solution x∗
of linear system
Ax = b,
as a fixed point of an application ϕ : Rn
→ Rn
:
ϕ(x∗
) = x∗
.
The fixed point algorithm constructs a xk defined by
x0 ∈ Rn
,
xk+1 = ϕ(xk ).
If the application ϕ is well chosen, then we have
lim
k→∞
xk = x∗
.
32 / 50

33. Example of 1 dimension
With the function of the form ϕ(x) = ax + b.
a 1 a 1
A necessary and sufficient condition for xk → x∗
is
|a| 1.
33 / 50

34. Contraction and existence of fixed point
Definition
An application ϕ : Rn
→ Rn
is a contraction for the norm ∥ · ∥, if there exists
λ 1 such that
∥ϕ(x) − ϕ(y)∥ ≤ λ∥x − y∥.
Theorem
Let ϕ : Rn
→ Rn
be a contraction and x0 ∈ Rn
. Then the sequence xk defined
by
x0 ∈ Rn
,
xk+1 = ϕ(xk ).
converges to the unique fixed point x∗
. Moreover,
(i)
Estimation a posteriori ∥x∗
− xk ∥ ≤ 1
1−λ ∥xk − xk+1∥;
(ii)
Estimation a priori ∥x∗
− xk ∥ ≤ λk
1−λ ∥x0 − x1∥.
34 / 50

35. Contraction and existence of fixed point
Proof :
1 It is sufficient to remark that
∥x∗
− xk ∥ ≤ ∥x∗
− xk+1 + xk+1 − xk ∥ ≤ ∥x∗
− xk+1∥ + ∥xk+1 − xk ∥
≤ ∥ϕ(x∗
) − ϕ(xk )∥ + ∥xk+1 − xk ∥
≤ λ∥x∗
− xk ∥ + ∥xk+1 − xk ∥.
2 With the inequality (1), we have
∥x∗
− xk ∥ ≤
1
1 − λ
∥xk+1 − xk ∥ ≤
1
1 − λ
∥ϕ(xk ) − ϕ(xk−1)∥
≤
λ
1 − λ
∥xk − xk−1∥ ≤
λk
1 − λ
∥x1 − x0∥.
35 / 50

36. Algorithm with a precision ε
Algorithm (Fixed point method)
Given : x0 ∈ Rn
, ε 0.
x1 = ϕ(x0), k = 1.
while ∥xk − xk−1∥ cε do
xk+1 = ϕ(xk )
k = k + 1
end while
Exercise
How to choose cε such that the algorithm stops with a precision of ε?
36 / 50

37. Application for the resolution of linear system
We are interested in the applications ϕ of the form
ϕ(x) = M−1
(Nx + b)
where A = M − N.
Exercise
Prove that if x∗
is a fixed point of ϕ, then
Ax∗
= b.
The application ϕ is a contraction if
|||M−1
N||| 1.
We remark that xk+1 = ϕ(xk ) is the solution of linear system
Mxk+1 = Nxk + b.
Idea : choose M close to A and easy to inverse.
37 / 50

38. Jacobi Method
The Jacobi method uses
M = D, N = −L − U.
Exercise
Prove
(xk+1)i =
1
aii

bi −
n
X
j=1,j̸=i
ai,j (xk )j

 .
Theorem
If A is diagonal strictly dominant, then the Jacobi method converges.
Theorem
If A is symmetric, ai,i 0, i = 1, . . . n, then the Jacobi method converges if
and only if A and 2D − A are positive definite.
38 / 50

39. Jacobi Method
Exercise
Find the convergent condition of the Jacobi method for the linear system
Ax = b.
A =


1 a a
a 1 a
a a 1


The principal minors of matrix A is ∆1 = 1, ∆2 = 1 − a2
,
∆3 = (1 − a)2
(1 + 2a). A is positive definite iff ∆2 0 and ∆3 0, which is
equivalent to −1
2 a 1.
2D − A =


1 −a −a
−a 1 −a
−a −a 1


The principal minors of matrix 2D − A is ∆1 = 1, ∆2 = 1 − a2
,
∆3 = (1 + a)2
(1 − 2a). 2D − A is positive definite iff ∆2 0 and ∆3 0,
which is equivalent to −1 a 1
2 .
Conclusion : the Jacobi method converges iff a ∈ (−1
2 , 1
2 ).
39 / 50

40. Gauss-Seidel Method
The Gauss-Seidel method uses
M = D + L, N = −U.
Exercise
Prove
(xk+1)i =
1
aii

bi −
i−1
X
j=1
ai,j (xk+1)j −
n
X
j=i+1
ai,j (xk )j

 .
Theorem
If A is symmetric positive definite, then the Gauss-Seidel method converges.
Exercise
Consider again the previous exercise, find the convergent condition of the
Gauss-Seidel method for the linear system Ax = b.
40 / 50

41. Gradient Method
Hypothesis : A is symmetric positive definite.
The principle is to search the solution x∗
of the linear system
Ax = b,
as the minimum of the energy
J(x) =
1
2
Ax, x − b, x ,
where Ax, x = xT
Ax, b, x = xT
b.
We construct then a sequence {xk }, which minimizes J as follows
x0 ∈ Rn
,
xk+1 = xk + αk rk , ∀k ≥ 1,
where rk is the descent direction and αk is the descent step.
41 / 50

42. Gradient Method
The choice of rk :
The direction rk is the opposite of the gradient of J, i.e.
rk = −∇J(xk ) = −(Axk − b) = b − Axk .
The choice of αk :
We choose αk as the step who minimizes J in the direction rk
J̃(α) = J(xk + αrk ).
With
J̃′
(α) = ∇J(xk + αrk ), rk
= A(xk + αrk ) − b, rk
= α Ark , rk − rk , rk ,
we deduce that
J̃′
(α) = 0 ⇐⇒ αk =
rk , rk
Ark , rk
.
42 / 50

43. Gradient Method
Algorithm (Gradient method)
1: Given : x0 ∈ Rn
, ε 0.
2: while ∥Axk − b∥ ε|||A−1
||| do
3: rk = b − Axk
4: αk = rk , rk / Ark , rk
5: xk+1 = xk + αk rk
6: end while
Example avec A = (1, 0; 0, 5), b = (0, 0)T
and x0 = (1, 0.2)T
.
43 / 50

44. Gradient Method
The drawback of the Gradient method:
Theorem
Assume the spectral of A is λ1 ≥ λ2 ≥ · · · ≥ λn 0, then we have
∥xk − x∗
∥A ≤
λ1 − λn
λ1 + λn
k
∥x0 − x∗
∥A
where ∥u∥A =
p
(Au, u).
When λ1 ≫ λn, the convergent rate of the gradient method is very slow.
44 / 50

45. Conjugate Gradient Method
Definition
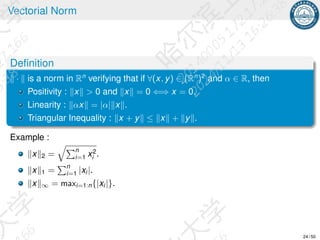
Assume A positive definite, if {p0, p1, . . . , pn−1} is Rn
, satisfying
Api , pj = 0, i ̸= j, then {p0, p1, . . . , pn−1} are A-conjugate.
Different from the gradient method, now we search the A-conjugate descent
directions.
Assume that the direction p0, p1, . . . , pk−1 are given and A-conjugate, we
search pk such that {p0, p1, . . . , pk } are A-conjugate. We decompose
x = y + αpk , where y ∈ span{p0, p1, . . . , pk−1}, α ∈ R.
J(x) = J(y + αpk )
= J(y) +
α2
2
Apk , pk −α b, pk , (since Ay, pk = 0)
min
x∈span{p0,p1,...,pk }
J(x) = min
y,α
J(y + αpk )
= min
y
J(y) + min
α
[
α2
2
Apk , pk −α b, pk ].
45 / 50

46. Conjugate Gradient Method
The solution of min
y
J(y) is y = xk .
The solution of min
α
[
α2
2
Apk , pk −α b, pk ] is
αk =
b, pk
Apk , pk
=
b − Axk , pk
Apk , pk
=
rk , pk
Apk , pk
.
Moreover, we assume that pk = rk + βk−1pk−1.
By using the fact pk , Apk−1 = 0, we obtain
βk−1 = −
rk , Apk−1
pk−1, Apk−1
.
46 / 50

47. Conjugate Gradient Method
Algorithm (Conjugate Gradient method)
1: Given : x0 ∈ Rn
, ε 0, r0 = b − Ax0, p0 = r0.
2: while ∥Axk − b∥ ε|||A−1
||| do
3: αk = rk , pk / Apk , pk
4: xk+1 = xk + αk pk
5: βk = − rk+1, Apk / pk , Apk
6: pk+1 = rk+1 + βk pk
7: end while
Example avec A = (1, 0; 0, 5), b = (0, 0)T
and x0 = (1, 0.2)T
.
47 / 50

48. Conjugate Gradient Method
Theorem
Assume the spectral of A is λ1 ≥ λ2 ≥ · · · ≥ λn 0, then we have
∥xk − x∗
∥A ≤ 2
√
λ1 −
√
λn
√
λ1 +
√
λn
k
∥x0 − x∗
∥A
where ∥u∥A =
√
Au, u .
Compare to the gradient method, the conjugate gradient method is much
better.
However, when λ1 ≫ λn, the convergent rate of the conjugate gradient
method is still very slow.
48 / 50

49. Complementary Exercises
Exercise
Compute the LU decomposition of matrix A:
A =


6 4 2
3 −2 −1
3 4 1


Exercise
Compute the LU decomposition of matrix A:
A =


1 2 3
4 5 6
7 8 10


49 / 50

50. Complementary Exercises
Exercise
Compute the Cholesky decomposition of matrix A:
A =


4 2 1
2 3 1
1 1 4


Exercise
Solve the following linear system by the Jacobi method and the Gauss-Seidel
method 

10 −1 −2
−1 10 −2
−1 −1 5




x1
x2
x3

 =


72
83
42


50 / 50