The document summarizes the Bisection method for finding roots of a continuous function. It presents the Bisection theorem, proves it in two parts: (1) that the absolute error decreases geometrically with each iteration, and (2) the sequence of midpoint estimates converges to the root. It also derives the error bound, showing the error approaches zero as the number of iterations increases, proving convergence of the Bisection method.

2. Bisection theorem analysis
State and prove the Bisection theorem
Find the error bound of the Bisection method

3. Presented by;
Hamza Nawaz CU-369-2017
Tauseef Ullah CU-358-2017
Salman Khan CU-384-2017
Waqar Ahmad CU-373-2017
Supervisor;
Madam Nudrat

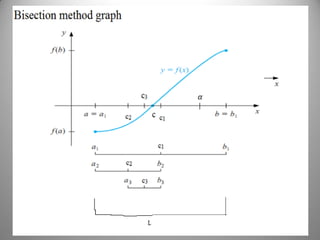
4. Bisection Method a quick overview
 Given a continuous function f (𝜘) on the interval [a , b] with
 f (a) ∙ f (b) < 0, there must be a root in (a, b).
 To find a root: set [𝑎1 , 𝑏1] = [a , b].
 Set 𝑐1 =
𝑎1+𝑏1
2
and compute f (𝑐1).
i. If f (𝑐1) = 0, then quit with root 𝑐1 (must be very lucky.)
ii. If (f (𝑎1) ∙ f (𝑐1) < 0), then set [𝑎2 , 𝑏2] = [𝑎1 , 𝑐1],
iii. Otherwise (f (𝑐1) ∙ f (𝑏1) < 0) set [𝑎2 , 𝑏2] = [𝑐1 , 𝑏1],
 Repeat with 𝑐2 =
𝑎2+𝑏2
2

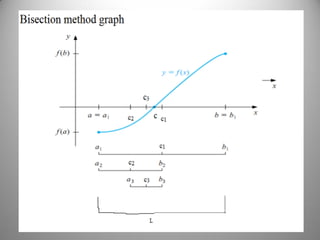
6. State and prove the Bisection theorem
• Statement:
 A function f (𝜘) is continuous on an interval [a, b]
 such that f (a) and f (b) have opposite sign, and
 the equation f (𝜘) = 0 has a real root 𝛼 in (a, b).
 If 𝑐 𝑛
∞
𝑛=0 is the sequence of midpoints of the intervals (which
brackets the root 𝛼), generated by the Bisection method then,
𝛼 − 𝑐 𝑛 ≤
𝑏 − 𝑎
2 𝑛+1 𝑓𝑜𝑟 𝑛 = 0,1,2, … …

7.  Further, the sequence 𝑐 𝑛
∞
𝑛=0 converges to the root 𝛼 :
lim
𝑛→∞
𝑐 𝑛 = 𝛼
 If there exists a root 𝛼 in the interval [a, b], then the distance
between any point 𝜘 in the interval [a, b] and the root is not
greater than the length of the interval, i.e.,
𝛼 − 𝜘 ≤ 𝑏 − 𝑎

8. Given:
 A function y = f (𝜘)
 For which f (𝜘) = f (a) or f (𝜘) = f (b)
 f (a) ∙ f (b) < 0
 f (α) = 0
 A sequence 𝑐 𝑛
∞
𝑛=0 converging to 𝛼
 𝛼 − 𝜘 ≤ 𝑏 − 𝑎
To prove:
1) 𝛼 − 𝑐 𝑛 ≤
𝑏−𝑎
2 𝑛+1 𝑓𝑜𝑟 𝑛 = 0,1,2, … …
2) lim
𝑛→∞
𝑐 𝑛 = 𝛼

10. • Proof:
 If L denotes the length of the recent root-bracketing interval
obtained by the Bisection method then
after first iteration, 𝐿1 =
1
2
𝑏 − 𝑎 =
𝑏−𝑎
2
and so on,
after nth iteration, 𝐿 𝑛 =
1
2
𝑏−𝑎
2 𝑛−1 =
𝑏−𝑎
2 𝑛
 Thus, any point 𝜘 in the root-bracketing interval after nth iteration is
not farther from the root than the length of the interval. That is,
𝛼 − 𝜘 ≤
𝑏 − 𝑎
2 𝑛

11.  Specifically, if 𝜘 = 𝑐 𝑛is the mid point of the most recent interval,
then the root 𝛼 is lying on either side of 𝑐 𝑛. Therefore,
𝛼 − 𝑐 𝑛 ≤ half of the length of the interval =
1
2
𝑏 − 𝑎
2 𝑛
𝛼 − 𝑐 𝑛 =
𝑏 − 𝑎
2 𝑛+1
Hence proved.
 This relation serves as the absolute error bound (maximum absolute
error) for the Bisection method.

12. Find the error bound of the Bisection method
 Let 𝜀 𝑛 denotes the error 𝛼 − 𝑐 𝑛. Assuming the error 𝜀 𝑛 after nth
iteration be equal to the maximum absolute error, then
𝜀 𝑛 =
𝑏 − 𝑎
2 𝑛+1
𝜀 𝑛 =
1
2
𝑏 − 𝑎
2 𝑛
=
1
22
𝑏 − 𝑎
2 𝑛−1
… =
1
2 𝑛
𝑏 − 𝑎
21
𝜀 𝑛 =
1
2 𝑛 𝜀0

13.  Note that, the right hand side of this relation would tend to be
zero as n becomes large.
 Hence, the error 𝜀 𝑛 approaches zero. That is,
lim
𝑛→∞
ℇ 𝑛 = lim
𝑛→∞
𝛼 − 𝑐 𝑛 = 0
lim
𝑛→∞
𝑐 𝑛 = 𝛼
Hence proved.
 Clearly, the Bisection method always converges.

14. Questions are welcome

15. AlhamdULilah