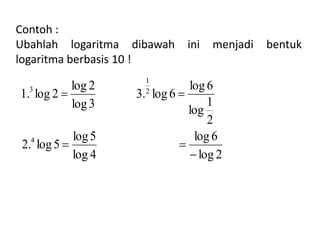
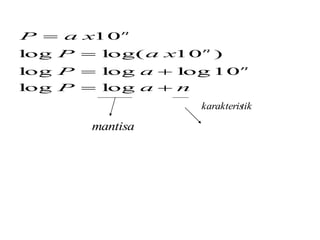
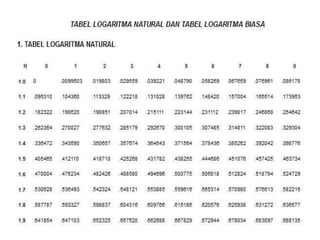
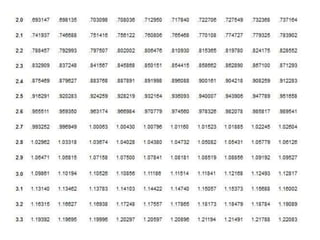
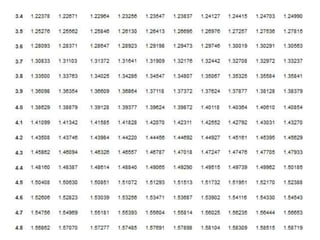
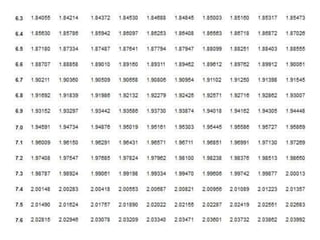
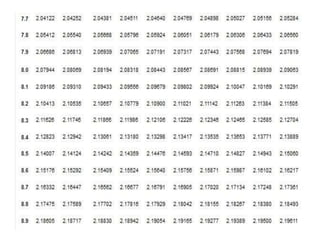
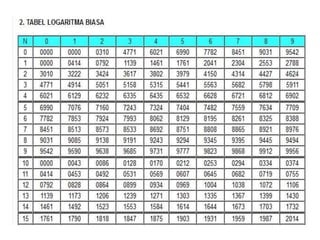
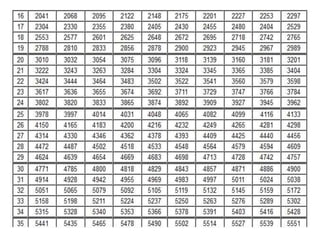
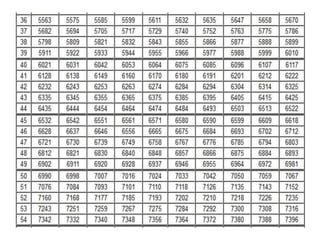
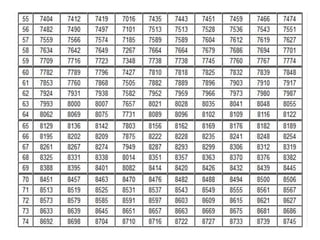
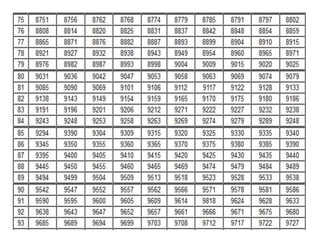
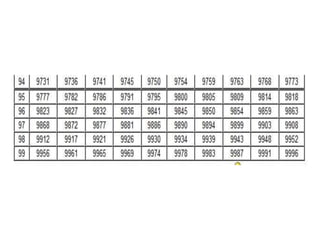
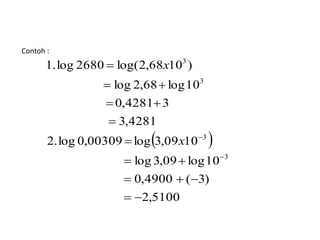Dokumen ini menjelaskan konsep dasar logaritma, termasuk definisi, sifat-sifat, dan cara penggunaannya dalam contoh perhitungan. Terdapat penjelasan tentang nilai logaritma berbasis 10 dan bagaimana mengkonversi logaritma dari basis lain. Juga dijelaskan cara menentukan antilogaritma dan karakteristik serta mantisa dalam nilai logaritma.

1. LOGARITMA
Oleh : Hidayati Rusnedy
SMA NEGERI 1 BANGKINANG KOTA

2. 1. Pengertian Logaritma
Plog a = m artinya a = pm
Keterangan:
p disebut bilangan pokok
a disebut bilangan logaritma atau numerus
dengan a > 0
m disebut hasil logaritma atau eksponen dari
basis

3. Logaritma dengan basis 10
Pada bentuk plog a = m, maka: 10log a = m
cukup ditulis log a = m.
Basis 10 pada logaritma tidak perlu dituliskan.
Contoh:
10log 3  dituliskan log 3
10log 5  dituliskan log 5

4. Sifat-sifat Logaritma
1. plog (a x b) = plog a + plog b
2. plog (a : b) = plog a - plog b
3. plog (a)n = n x plog a
m
n am = plog (a) n
4. plog
= m plog a
n

5. Contoh
1. Jika 2log x = 3
Tentukan nilai x = ….
Jawab:
2log x = 3  x = 23
x = 8.
2. Jika 2log x = 3
Tentukan nilai x = ….
Jawab:
2log x = 3  x = 23
x = 8.

6. 3. Nilai dari 2log (8 x 16) = …
Jawab:
= 2log 8 + 2log 16
= 2log 23 + 2log 24
= 3 + 4
= 7
4. Nilai dari 3log (81 : 27) = …
Jawab:
= 3log 81 - 3log 27
= 3log 34 - 3log 33
= 4 - 3
= 1

7. 5. Nilai dari 2log 84 = ….
Jawab:
= 2log 84
= 4 x 2log 23
= 4 x 3
= 12
6. Nilai dari 2log 84 = ….
Jawab:
= 2log 84 
= 2 x 2log 23
= 2 x 3
= 6
= 4 2log 8
2

8. Menentukan Logaritma Suatu Bilangan
Kita bisa menggunakan Tabel Logaritma atau
Kalkulator.
Walaupun kedua alat tersebut hanya
memberikan nlai logaritma untuk untuk
bentuk berbass 10, kita selalu dapat
mengubah bentuk logartma berbasis
berapapun kebentuk logartma berbasis 10.

9. Contoh :
Ubahlah logaritma dibawah ini menjadi bentuk
logaritma berbasis 10 !
log 6
1
log 6
log 2
log 2
 
log 5
log 4
2. log 5
2
log
1
3. log 6
log 3
1. log 2
4
2
3

 

10. Hasil logaritma suatu bilangan merupakan
blangan yang terdiri dari 2 bagian, yaitu bagian bulat
(KARAKTERISTIK) dan bagian desimal (MANTISA).
Pada tabel logaritma hanya bagian desimalnya
saja sedangkan karakteristiknya tidak tertulis dan kita
tentukan sendiri.
Untuk itu kita harus merubah ke bentuk baku
misal
P= a dengan a dan n bilanganbulat n 10 , 1 10 

11. P a x
10
P a x
log 
log( 10 )
P a
log  log 
log10
P a n
n
n
n
 

log log
mantisa
karakteristik

12. Contoh :
1.log 2680 log(2,68 10 )
3

 
log 2,68 log10
 
0,4281 3
3,4281
 
2.log 0,00309 
log 3,09 10
 
log 3,09 log10
  
0,4900 ( 3)
2,5100
3
3
3
 


 x
x

13. Menentukan Antilogaritma suatu bilangan
Misalkan log x=y maka
x=antilog y
y 10
10
2,95
2
10 . log 0,95
100.(8,913)
891,3




anti
Jadi,antilog y =
x
Contoh:
1. Log x=0.123 maka x = antilog 0,123
x = 1,327
2. Log x= 2,95 maka x = antilog 2,95