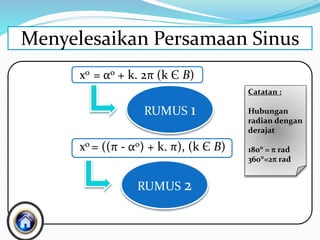
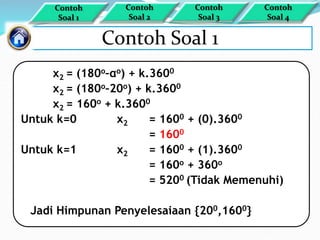
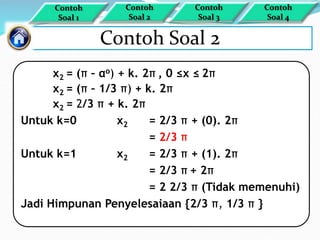
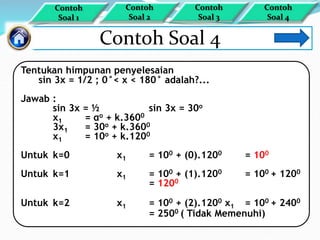
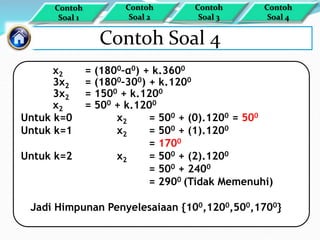
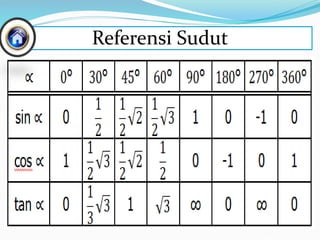
Dokumen ini membahas tentang penyelesaian persamaan sinus dengan berbagai rumus dasar dan contoh soal terkait. Metode yang digunakan termasuk hubungan antara derajat dan radian serta pembuktian trigonometri. Himpunan penyelesaian disampaikan melalui beberapa contoh spesifik dengan penerapan rumus dalam rentang yang ditentukan.

2. MENU UTAMA
MATERI UTAMA
REFERENSI
SUDUT
LATIHAN
CONTOH SOAL

3. Menyelesaikan Persamaan Sinus
Jika Sin x0 = sin 0 (x Є R ), maka :
x0 =  + k.3600, atau
x0 = (1800-0) + k.3600
Jika Sin x0 = sin 0(x Є R ), maka :
x0 = 0+ k.2π, atau
x0 = (π-0) + k.2π, k Є B
Next

4. Contoh Soal
Contoh Soal 1
Contoh Soal 4
Contoh Soal 3
Contoh Soal 2

5. Karena Sinus berharga positif hanya
berada di kuadran I, kuadran II dan
lebih dari kuadran IV.
Kuadran I
Kuadran <IV
Kuadran II
Menyelesaikan Persamaan Sinus
Next

6. Sin αo = sin αo
Maka :
Sin αo = sin αo
αo = αo
Menu Sub Bab

7. Sin αo = sin (180o – αo)
Maka :
Sin αo = sin (180o – αo)
αo = 180o – αo
Menu Sub Bab
Pembuktian

8. Sin αo = sin (180o – αo)
Pembuktian :
Sin αo = sin (180o – αo)
Menggunakan rumus trigonometri jumlah dan selisih
dua sudut
Sin (  )  sin  cos   cos  sin 
Maka :
Sin αo = sin 180o cos αo – cos 180o sin αo
Sin αo = (0) cos αo – (-1) sin α0
Sin αo = sin αo (Terbukti)
Maka :
αo = 180o – αo
Menu Sub Bab Pembuktian

9. Sin αo = sin (αo + k. 360o)
Maka :
Sin αo = sin (αo + k. 360o)
αo = αo + k. 360o
Menu Sub Bab
Pembuktian

10. Sin αo = sin (αo + k. 360o)
Pembuktian :
Sin αo = sin (αo + k. 360o)
Menggunakan rumus trigonometri jumlah dan selisih
dua sudut
Sin ( + )  sin  cos  + cos  sin 
Maka :
Sin αo = sin αo cos (k.360o) + cos αo sin (k.360o)
Menu Sub Bab Pembuktian

11. Sin αo = sin αo cos (k.360o) + cos αo sin (k.360o)
Jika k = 0
Sin αo = sin αo cos (k.360o) + cos αo sin (k.360o)
Sin αo = sin αo cos (0.360o) + cos αo sin (0.360o)
Sin αo = sin αo cos 0o + cos αo sin 0o
Sin αo = sin αo (1) + cos αo sin (0)
Sin αo = sin αo (Terbukti)
Menu Sub Bab Pembuktian

12. Sin αo = sin αo cos (k.360o) + cos αo sin (k.360o)
Jika k = 1
Sin αo = sin αo cos (k.360o) + cos αo sin (k.360o)
Sin αo = sin αo cos (1.360o) + cos αo sin (1.360o)
Sin αo = sin αo cos 360o + cos αo sin 360o
Sin αo = sin αo (1) + cos αo sin (0)
Sin αo = sin αo (Terbukti)
Menu Sub Bab Pembuktian

13. Jika sin xo = sin αo (x Є R ), maka :
xo = αo
Karena αo = αo + k. 360o
Maka :
xo = αo + k. 360o (k Є B)
Menyelesaikan Persamaan Sinus
RUMUS 1

14. xo = αo + k. 360o (k Є B) Rumus 1
Karena αo = 180o – αo
Maka :
xo = ((180o- αo) + k. 360o), (k Є B)
Menyelesaikan Persamaan Sinus
RUMUS 2

15. xo = αo + k. 360o (k Є B)
xo = ((180o- αo) + k. 360o), (k Є B)
Menyelesaikan Persamaan Sinus
RUMUS 2
RUMUS 1

16. xo = αo + k. 2π (k Є B)
xo = ((π - αo) + k. π), (k Є B)
Menyelesaikan Persamaan Sinus
RUMUS 2
RUMUS 1
Catatan :
Hubungan
radian dengan
derajat
180 =  rad
360=2 rad

17. Contoh Soal 1
Tentukan himpunan penyelesaian
sin x = sin 200 ; 0 ≤x ≤3600 adalah?...
Jawab :
sin x = sin 200 ; 0 ≤x ≤3600
x1 = αo + k.3600
x1 = 20o + k.3600
Untuk k=0 x1 = 200 + (0).3600
= 200
Untuk k=1 x1 = 200 + (1).3600
= 200 + 3600
= 3800 (Tidak memenuhi)
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

18. Contoh Soal 1
x2 = (180o–αo) + k.3600
x2 = (180o–20o) + k.3600
x2 = 160o + k.3600
Untuk k=0 x2 = 1600 + (0).3600
= 1600
Untuk k=1 x2 = 1600 + (1).3600
= 160o + 360o
= 5200 (Tidak Memenuhi)
Jadi Himpunan Penyelesaiaan {200,1600}
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

19. Contoh Soal 2
Tentukan himpunan penyelesaian
sin x = sin 1/3 π ; 0 ≤x ≤ 2π adalah?...
Jawab :
sin x = sin 1/3 π; 0 ≤x ≤ 2π
x1 = αo + k. 2π
x1 = 1/3 π + k. 2π
Untuk k=0 x1 = 1/3 π + (0). 2π
= 1/3 π
Untuk k=1 x1 = 1/3 π + (1). 2π
= 1/3 π + 2π
= 2 1/3 π (Tidak memenuhi)
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

20. Contoh Soal 2
x2 = (π – αo) + k. 2π , 0 ≤x ≤ 2π
x2 = (π – 1/3 π) + k. 2π
x2 = 2/3 π + k. 2π
Untuk k=0 x2 = 2/3 π + (0). 2π
= 2/3 π
Untuk k=1 x2 = 2/3 π + (1). 2π
= 2/3 π + 2π
= 2 2/3 π (Tidak memenuhi)
Jadi Himpunan Penyelesaiaan {2/3 π, 1/3 π }
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

21. Contoh Soal 3
Tentukan himpunan penyelesaian
sin x = 1/2 ; 0 ≤x ≤3600 adalah?...
Jawab :
sin x = ½ ; 0 ≤x ≤3600
sin x = 30o
x1 = αo + k.3600
x1 = 30o + k.3600,
Untuk k=0 x1 = 300 + (0).3600
= 300
Untuk k=1 x1 = 300 + (1).3600
= 300 + 3600
= 3900 (Tidak memenuhi)
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

22. Contoh Soal 3
x2 = (1800–αo) + k.3600
x2 = (1800–30o) + k.3600
x2 = 1500 + k.3600
Untuk k=0 x2 = 1500 + (0).3600
= 1500
Untuk k=1 x2 = 1500 + (1).3600
= 1500 + 3600
= 5200 (Tidak Memenuhi)
Jadi Himpunan Penyelesaiaan {300,1500}
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

23. Contoh Soal 4
Tentukan himpunan penyelesaian
sin 3x = 1/2 ; 0°< x < 180° adalah?...
Jawab :
sin 3x = ½ sin 3x = 30o
x1 = αo + k.3600
3x1 = 30o + k.3600
x1 = 10o + k.1200
Untuk k=0 x1 = 100 + (0).1200 = 100
Untuk k=1 x1 = 100 + (1).1200 = 100 + 1200
= 1200
Untuk k=2 x1 = 100 + (2).1200 x1 = 100 + 2400
= 2500 ( Tidak Memenuhi)
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

24. Contoh Soal 4
x2 = (1800–α0) + k.3600
3x2 = (1800–300) + k.1200
3x2 = 1500 + k.1200
x2 = 500 + k.1200
Untuk k=0 x2 = 500 + (0).1200 = 500
Untuk k=1 x2 = 500 + (1).1200
= 1700
Untuk k=2 x2 = 500 + (2).1200
= 500 + 2400
= 2900 (Tidak Memenuhi)
Jadi Himpunan Penyelesaiaan {100,1200,500,1700}
Contoh
Soal 1
Contoh
Soal 4
Contoh
Soal 3
Contoh
Soal 2

25. Latihan

26. Referensi Sudut