1. A linear transformation is a function between vector spaces that preserves vector addition and scalar multiplication. 2. To be a linear transformation, T(u+v) must equal T(u)+T(v) and T(αu) must equal αT(u) for any vectors u,v and scalar α. 3. Properties of linear transformations include: the zero vector maps to the zero vector; the image of a linearly independent set is linearly independent; and the image of any subspace is a subspace. The transformation is determined by its effect on a basis.

1. GP 116: Linear Algebra
Class Notes
Linear Transformations
Part 1
Dr. R. Palamakumbura

2. Linear Transformations
• You have already learnt about vector spaces.
• In this section we will learn about special type of
functions defined on vector spaces, that preserve the
algebraic structure of the space (addition and scalar
multiplication).
• These functions are called linear transformations and
we will see a close relationship with matrices and such
transformations.

3. Linear Transformations
• Definition: Linear Transformation
Let and be vector spaces over a field . Then a
transformation
that preserves the operations of addition,
and scalar multiplication,
is defined as a linear transformation.
𝒱 𝒲 ℱ
T : 𝒱 → 𝒲
T(u + v) = T(u) + T(v); u, v ∈ 𝒱
T(αu) = αT(u); u ∈ 𝒱, α ∈ ℱ

4. Linear Transformations
• Note:
1. In T(u+v)=T(u)+T(v), the symbol + in the left side denotes addition
in and the symbol + in the right side denotes addition in .
2. Both domain and codomain have to be vector space over the
same field.
3. If the domain and codomain is the same vector space then such
a linear transformation is called a linear operator.
𝒱 𝒲

5. Linear Transformations
• Some Examples:
1. Identity transformation,
For
2. For k>0, stretching or contraction,
For
3. Reflection through the x-axis,
For
T : ℜ ↦ ℜ, T(x) = x .
x, y ∈ ℜ; T(x + y) = x + y = T(x) + T(y), T(αx) = αx = αT(x) .
T : ℜ2
↦ ℜ2
, T(x) = (kx1, kx2), x = (x1, x2) ∈ ℜ2
.
x, y ∈ ℜ; T(x + y) = (k(x1 + y1), k(x2 + y2)) = (kx1, kx2) + (ky1, ky2)
= T(x) + T(y)
T(αx) = (kαx1, kαx2) = αT(x) .
T : ℜ2
↦ ℜ2
, T(x) = (x1, − x2), x = (x1, x2) ∈ ℜ2
.
x, y ∈ ℜ; T(x + y) = ((x1 + y1), − (x2 + y2)) = T(x) + T(y)
T(αx) = (αx1, − αx2) = αT(x) .

6. Linear Transformations
• Some Examples:
4. Counter clockwise rotation,
5. For shearing,
6. Projection on to the x-axis,
Exercise: Show that these are linear transformations.
T: ℜ2
↦ ℜ2
T(x) = (x1 cos θ − x2 sin θ, x1 sin θ + x2 cos θ), x = (x1, x2) ∈ ℜ2
.
k ≠ 0,
T : ℜ2
↦ ℜ2
, T(x) = (x1 + kx2, x2), x = (x1, x2) ∈ ℜ2
.
T : ℜ2
↦ ℜ2
, T(x) = (x1,0), x = (x1, x2) ∈ ℜ2
.

7. Linear Transformations

8. Linear Transformations
• Some Examples:
7. Derivative of a polynomial,
8. Integral of a polynomial,
9. Transpose of a matrix,
10. Trace of a matrix,
Exercise: Show that these are linear transformations.
T : 𝒫n ↦ 𝒫n, T(p(x)) = D(p(x)) = p′(x) .
T : 𝒫n ↦ 𝒫n+1, T(p(x)) =
∫
x
a
p(x)dx .
T : ℳm×n ↦ ℳn×m, T(M) = MT
.
T : ℳn×n ↦ ℜ, T(M) = trace(M) .

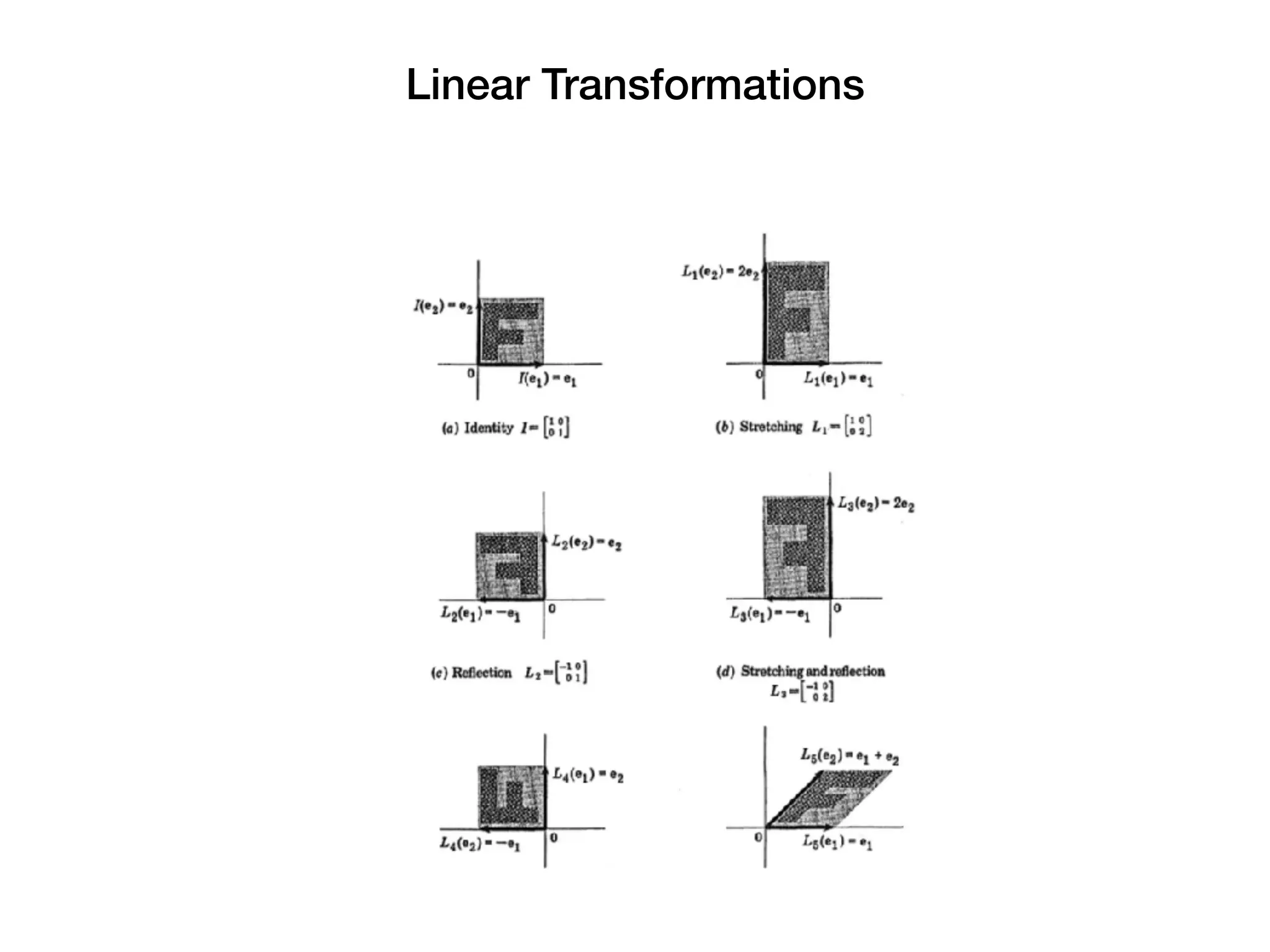
9. Linear Transformations
The following are not linear transformations.
1. Translation,
For
2. Quadratic function,
3. Trigonometric functions,
4. Determinant,
Exercise: Show that 2-4 are not linear transformations.
T : ℜ ↦ ℜ, T(x) = x + a, a ≠ 0.
x, y ∈ ℜ, T(x + y) = x + y + a ≠ (x + a) + (y + a) = T(x) + T(y) .
T : ℜ ↦ ℜ, T(x) = x2
.
T : ℜ ↦ [−1,1], T(x) = sin x .
T : ℳn×n ↦ ℜ, T(M) = det(M) .

10. Linear Transformations
• Properties:
Let be a linear transformation.
1. T sends zero vector of to the zero vector of . That is
2. T(-v)=-T(v) and T(u-v)=T(u)-T(v)
3. Under T, the image of a linearly independent set is linearly
independent. That is if is linearly independent then is
linearly independent.
4. Under T, the image of any subspace of the domain is a subspace of
the codomain. That is if is a subspace then is a
subspace.
T : 𝒱 ↦ 𝒲
𝒲
𝒱
T(0𝒱) = 0𝒲 .
𝒮 ⊂ 𝒱 T(𝒮)
𝒮 ⊂ 𝒱 T(𝒮) ⊂ 𝒲

11. Linear Transformations
• Properties:
7.For T, the inverse of a subspace of the codomain is a
subspace of the domain. That is if is a subspace
then is a subspace.
8.The rule for T is completely determined by its effect on a
basis for .
𝒮 ⊂ 𝒲
T−1
(𝒮) ⊂ 𝒱
𝒱

12. Linear Transformations
• Examples: These examples will explain the properties defined earlier.
Consider the linear transformation:
1. Consider subspace of the domain
Note that any vector in is of the form
Now since T is linear
Therefore image is a line through the origin and the point (1,1,0) and is a
subspace of the codomain.
2. Let be the standard basis for the domain.
Since T is linear
Therefore basis vectors completely determines T.
T: ℜ3
↦ ℜ3
T(x) = T(x1, x2, x3) = (x1 + x2, x1 + x3,0)
𝒮 = span{(1,0,0)} .
𝒮 v = α(1,0,0) .
T(v) = αT(1,0,0) = α(1,1,0) .
ℬ = {e1, e2, e3} x = x1e1 + x2e2 + x3e3
T(x) = x1T(e1) + x2T(e2) + x3T(e3)
= x1(1,1,0) + x2(1,0,0) + x3(0,1,0)