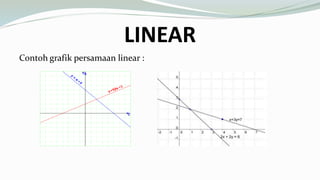
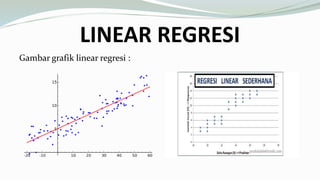
Sistem nonlinier membahas tentang pengertian linear, regresi, dan regresi linear. Persamaan linear memiliki sifat bahwa setiap suku hanya mengandung satu variabel dan dapat digambarkan dalam grafik kartesius. Regresi digunakan untuk melihat hubungan antara dua atau lebih variabel. Regresi linear adalah pendekatan untuk memodelkan hubungan antara variabel dependen dan satu atau lebih variabel independen.