Dokumen tersebut merangkum konsep sistem linier dan non-linier, serta proses linearisasi untuk menganalisis sistem non-linier. Ia menjelaskan bahwa sistem linier memenuhi hukum superposisi sedangkan sistem non-linier sulit diprediksi, kemudian mendefinisikan analisis regresi sebagai metode untuk melinearisasi sistem non-linier dengan mendekati datanya dengan fungsi linier atau non-linier sederhana.

1. Linearisasi
Disusun Oleh:
Rizki Adi Nugroho (1410501075)
Dosen Pembimbing:
R. Suryoto Edy Raharjo, S.T., M.Eng.

2. Linearisasi
• Sistem
• Sistem Linier
• Sistem Non-Linier
• Linearisasi

3. Sistem
• Berbicara tentang sistem berarti berbicara tentang sekumpulan elemen/unsur
yang menyusun sistem, dan berbicara tentang cara berhubungan antara
elemen-elemen penyusun itu. Umumnya pengertian sistem menyangkut
sesuatu yang tersusun dari elemen-elemen. Jadi sebuah komponen tidak
dapat disebut sistem. Tapi secara mikroskopis, sebuah elemen juga tersusun
dari elemen-elemen yang lebih kecil sehingga dapat disebut sistem juga.
Elemen-elemen penyusun sistem mempunyai perilaku yang khas dalam
sistem, atau mempunyai tugas yang spesifik yang tidak dapat digantikan oleh
elemen lain. Jika sebuah elemen penyusun sistem tidak ada, maka sistem
menjadi tidak ada atau sistem berganti menjadi sistem lain.

4. Sistem Elemen Fungsi elemen
Sistem audio
Mekanik playback
Mengubah sinyal magnetis dari kaset ke sinyal
elektris
Penguat Memperkuat sinyal elektris
Speaker
Mengubah sinyal elektris menjadi sinyal
suara/audio
Tombol volume Mengubah penguatan penguat
Tata surya
Matahari Pusat tata surya
Planet Mengitari pusat tata surya
Satelit Mengitari planet
Tabel ini mendaftar contoh beberapa sistem berikut elemen penyusun dan fungsi setiap elemen

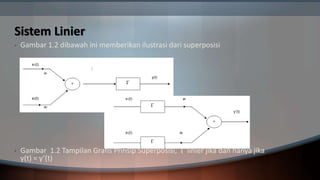
5. Sistem Linier
Sistem linier adalah sistem yang memenuhi hukum superposisi. Prinsip superposisi
adalah respons sistem (keluaran) terhadap jumlah bobot sinyal akan sama dengan
jumlah bobot yang sesuai dari respon (keluaran) sistem terhadap masing-masing sinyal
masukan individual. Karena itu linieritas dapat didefinisikan sebagai berikut.
Teorema : Sistem adalah linier jika dan hanya jika
[a1x1(t) + a2x2(t)] = a1 [x1(t)] + a2 [x2(t)] (1.3)
untuk setiap deret masukan x1(t) dan x2(t) yang berubah-ubah dan setiap konstanta a1
dan a2 yang berubah-ubah.

6. Sistem Linier
• Gambar 1.2 dibawah ini memberikan ilustrasi dari superposisi
• Gambar 1.2 Tampilan Grafis Prinsip Superposisi,  linier jika dan hanya jika
y(t) = y’(t)

7. Sistem Nonlinier
• Suatu sistem yang sifatnya tidak tetap, mudah berubah, sulit dikontrol, dan
sulit diprediksi. Selain itu bila suatu fungsi sistem linear digambarkan pada
grafik dan ditarik suatu garis tidak akan membentuk garis lurus.
• Sistem semacam ini memiliki tingkat ke-sensitivitas-an yang sangat tinggi.
• Bila di gambarkan dengan bagan :

8. Linearisasi
Keterangan :
• Dalam bagan tersebut dapat diamati 2 hal, yaitu:
• pertama, bahwa input-input yang berlainan dalam suatu proses dapat
menghasilkan output yang sama.
• kedua, bahwa satu input yang ada dalam suatu proses dapat memberikan
output yang sama.
• Sistem yang ada di alam semesta ini terbagi menjadi 2 macam sistem,
yaitu sistem linear dan sistem non-linear. Sekitar lebih dari 80% kejadian
dan fenomena yang terjadi di alam semesta ini merupakan suatu bentuk
dari sistem non-linear.
•

9. Linearisasi
• Regresi merupakan bagian dari linearisasi.
• Regresi merupakan metode analisis yang digunakan untuk melihat pengaruh
antara dua atau lebih variabel.
• Pada analisis regresi variabel dibedakan menjadi dua bagian:
- variabel respons (response variable) atau biasa juga disebut variabel
bergantung (dependent variable)
- variabel explanory atau biasa disebut variable) atau disebut juga
variabel bebas (independent variabel).
•

10. Linearisasi
• Regresi juga di bagi menjadi 2 yaitu :
- Regresi Linear :
 Regresi Linear Sederhana
 Regresi Linear Berganda
- Regresi Non Linear :
 Regresi Eksponensial

11. Linearisasi
• Fungsi analisis regresi :
• Untuk mengetahui pengaruh dari sebuah variabel atau lebih dari beberapa
variabel bebas terhadap variabel respon.
• Untuk memprediksi pengaruh dari sebuah variabel atau lebih dari beberapa
variabel bebas terhadap variabel respon.
• Untuk mengukur kekuatan hubungan antara variabel bebas dan variabel
respon.

12. Linearisasi
A. REGRESI LINEAR
• Misalkan (xi, yi) adalah data hasil pengukuran, kita akan menghampiri
titik tersebut dengan sebuah garis lurus. Garis lurus tersebut dibuat
sedemikian sehingga errornya sekecil mungkin dengan titik-titik data.
• Karena data mengandung error, maka nilai data sebenarnya, g(xi) dapat
ditulis sbb : g(xi) = yi + ei i = 1, 2, 3, .., n dalam hal ini ei adalah error
setiap data .
• Diinginkan untuk membentuk fungsi linier :

13. Linearisasi
• Yang mencocokkan data sedemikian sehingga deviasinya :
• Total kuadrat deviasinya adalah :
• Agar R minimum, maka haruslah

14. Linearisasi
• Masing-masing ruas kedua persamaan dibagi dengan -2 :
• Dalam bentuk matriks :

15. Linearisasi
• Tentukan persamaan garis lurus yang mencocokkan data pada tabel dibawah
ini.
Kemudian perkirakan nilai y untuk x = 1.0
Penyelesaian :

16. Linearisasi
• Diperoleh persamaan linear :
Maka didapatkan hasil :
a = 0.28616 b = 1.76456
Persamaan garis regresi f(x) = 0.28616 + 1.76256x

17. Linearisasi
B. REGRESI NON LINEAR
Meskipun fungsi hampiran berbentuk non linier, namun pencocokan kurva dengan fungsi non linier
tersebut dapat diselesaikan juga diselesaikan dengan cara regresi linier
Misalnya 2 macam fungsi non linear berikut ini :
1. Persamaan pangkat sederhana y = Cxb, C dan b konstanta
2. Model Eksponensial y = Cebx, C dan b konstanta
Contoh :
- model pertumbuhan populasi
- model peluruhan zat radioaktif

18. Daftar Pustaka
• http://tanya-ilmukomputer.blogspot.co.id/2014/11/konsep-dasar-sistem-
linier-perbedaan_7.html
• http://ririnbelajarlinier.blogspot.co.id/2014/11/sistem-linier-dan-non-linier.html
• https://en.wikipedia.org/wiki/Nonlinear_system
• http://googebra.blogspot.co.id/2014/11/sistem-persamaan-non-linear.html
• http://mn.uio.no/ifi/english/services/knowledge/cs/forelesn.kap4.pdf
• https://id.scribd.com/presentation/97435760/Sistem-Linier6
• http://jati.stta.ac.id/2015/07/komputasi-numeris-analisis-regresi_26.html
• http://irma.lecturer.pens.ac.id/Metode%20Numerik/MetNum07-Regresi.pdf
• http://www.pengertianahli.com/2014/07/pengertian-regresi-apa-itu-regresi.html
• https://willyoctora.wordpress.com/2013/07/09/kajian-analisa-regresi/

19. TERIMA KASIH