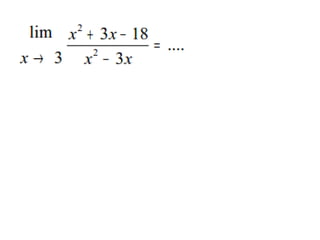Dokumen ini membincangkan konsep limit dalam fungsi aljabar, termasuk pengertian limit, teorema limit, dan metode penyelesaian. Ia menjelaskan cara menghitung nilai limit ketika x mendekati nilai tertentu serta tak hingga, dan melibatkan pemakaian teorema limit dengan berbagai contoh. Selain itu, dokumen ini juga memberikan latihan untuk pemahaman lebih lanjut mengenai topik limit.

1. Limit

2. Limit Fungsi
Aljabar
Limit Fungsi
Aljabar
Peta
Konsep
Limit
Fungsi
Teorema
Limit
Metode
Penyelesaian
Pengertian Limit
Limit fungsi yang
tidak memiliki nilai
limit
Limit fungsi untuk
x →∞
Metode substitusi
Metode faktorisasi
Metode perkalian
bilangan sekawan
Menentukan
nilai Limit
dengan Aljabar
Bentuk tak tentu
Bentuk tak tentu
Bentuk tak tentu
dan
~
~  0
0
c
k

o
o
~
~

3. Mengapa ada teorema limit?

8. Pengertian Limit
Limit fungsi f(x) adalah suatu nilai yang didekati
oleh fungsi f(x) jika x mendekati suatu nilai tertentu.
Misal untuk x mendekati a maka f(x) mendekati L.
Istilah mendekati dinotasikan dengan “”
L
f(x)
lim
a
x


X mendekati a
fungsi
Nilai limit
Cara membaca :
Limit f(x) = L
untuk x mendekati
a

9. Pengertian Limit
Limit fungsi f(x) adalah suatu nilai yang didekati
oleh fungsi f(x) jika x mendekati suatu nilai tertentu.
Misal untuk x mendekati a maka f(x) mendekati L.
Istilah mendekati dinotasikan dengan “”
L
f(x)
lim
a
x


X mendekati a
fungsi
Nilai limit
Cara membaca :
Limit f(x) = L
untuk x mendekati
a

10. Pengertian Limit
Limit fungsi f(x) adalah suatu nilai yang didekati
oleh fungsi f(x) jika x mendekati suatu nilai tertentu.
Misal untuk x mendekati a maka f(x) mendekati L.
Istilah mendekati dinotasikan dengan “”
L
f(x)
lim
a
x


X mendekati a
fungsi
Nilai limit
Cara membaca :
Limit f(x) = L
untuk x mendekati
a

11. Selidikilah nilai limit fungsi untuk x
mendekati tak hingga.
Kesimpulan :
x f(x)
100
1.000
10.000
100.000
1.000.000
1,01
1,001
1,0001
1,00001
1,000001
*Semakin besar nilai x,
maka nilai f(x) akan semakin
dekat dengan 1
Limit Fungsi Untuk X →∞

12. Teorema 1
k
k
lim
a
x


7
7
lim
8
x


Contoh :
5
5
lim
0
x


Teorema 2
a
x
lim
a
x


-2
x
lim
-2
x


Contoh :
0
x
lim
0
x


Teorema 3
kx
lim
a
x


Contoh :
k . a
x
k lim
a
x


3x
lim
-2
x


3 . (-2) = -6
x
3 lim
-2
x


0
lim

x


Teorema 4
0
lim

x


Contoh :
n
x
k
2
7
x

13. Teorema 5
[f(x) + g(x)]
lim
a
x


Contoh :
f(x)
lim
a
x
g(x)
+ lim
a
x
[f(x) - g(x)]
lim
a
x


f(x)
lim
a
x
g(x)
- lim
a
x
[3x + 6]
lim
2
x


3x
lim
2
x
6
+ lim
2
x
x
3. lim
2
x
6
+ lim
2
x

 3. 2 + 6
 12
Contoh :
[4x -7]
lim
0
x


4x
lim
0
x
7
- lim
0
x
x
4. lim
0
x
7
- lim
0
x

 4. 0 - 7
 -7

14. Teorema 6
[f(x) . g(x)]
lim
a
x


Contoh :
f(x)
lim
a
x
g(x)
. lim
a
x
x2
lim
2
x


x) .
(lim
2
x

Contoh :
[4x . 7x]
lim
1
x


4x
lim
1
x
7x
. lim
1
x
x
4. lim
1
x
x
. 7 lim
1
x

 (4 . 1) . (7 .1)
 4.7
 28
x . x
lim
2
x 
x)
(lim
2
x
 2 . 2

15. Teorema 7
f(x)
lim
a
x 

f(x)
lim
a
x
g(x)
lim
a
x
g(x)
x - 1
lim
4
x 

(x – 1)
lim
4
x
(x – 3)
lim
4
x
x - 3

3

4 - 1
4 - 3
Contoh :
Teorema 8
[f(x)]n
lim
a
x


f(x) ]n
[lim
a
x


[2x-1]3
lim
3
x


(2x-1)]3
[lim
3
x


 [2 . 3 – 1]3
 53
 125

16. LATIHAN SOAL