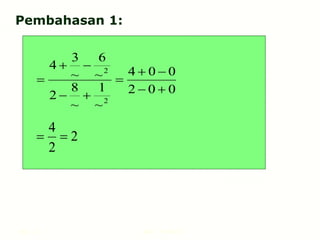
Dokumen ini membahas konsep limit fungsi aljabar dan trigonometri, termasuk langkah-langkah untuk menghitung limit dan teorema dasar tentang limit. Terdapat juga contoh soal dan pembahasan untuk membantu pemahaman mengenai nilai limit dari fungsi-fungsi tertentu. Struktur dokumen ini mencakup prosedur dan metode penyelesaian berbagai bentuk limit.

1. LIMITFUNGSIALJABAR
dan
LIMITFUNGSITRIGONOMETRI
KELOMPOK 5:
FEBYKESWANTO
LIA
SUPRIYANITASARI
TRIANA ELIN

2. LIMITFUNGSI:
Mendekatihampir,sedikitlagi,atauhargabatas

3. Limit fungsi:
Suatu limit f(x) dikatakan
mendekati a
{f(x) a} sebagai suatu limit.
Bila x mendekati a {x a}
Dinotasikan
Lim f(x) = a
x a

4. Langkat-langkahmengerjakanlimitfungsi
(supayabentuktaktentudapatdihindari)
adalah….
1. Subtitusilangsung.
2. Faktorisasi.
3. Mengalikandenganbilangansekawan.
4. Membagidenganvariabelpangkattertinggi.

5. Berapateoremalimit:
Bila Lim f(x) = A dan Lim g(x) = B
x a x a
Maka
1. Lim [k.f(x)] = k Lim f(x)
x a x a
= k. A
2. Lim [f(x)+g(x)] = Lim f(x) + Lim g(x)
x a x a x a
= A + B

6. 3. Lim {f(x) x g(x)}
x a x a
= Lim f(x) x Lim g(x)
x a x a
= A x B
4. B
A
x
g
x
f
x
g
x
f
Lim
Lim
Lim
a
x
a
x
a
x










 )
(
)
(
)
(
)
(

7. Hal.: 7 LIMIT FUNGSI
  n
n
a
x
n
a
x
A
x
f
x
f Lim
Lim 









)
(
)
(
5.
6.
A
x
f
n
a
x
n
n
a
x
Lim
x
f
Lim 



)
(
)
(

8. Soal latihan:
1. Nilai dari Lim 3x adalah….
x 2
Limit fungsi aljabar

9. Hal.: 9 LIMIT FUNGSI
Pembahasan 1:
Lim 3x = 3(2)
x 2
= 6
Pembahasan 2:
Lim 3x = 3 Lim X
x 2 x 2
= 3(2) = 6

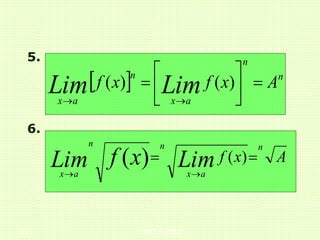
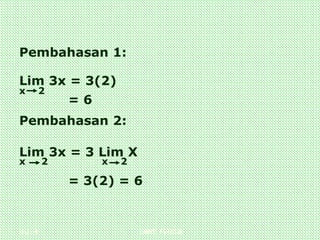
10. 2. Nilai dari Lim [6x-2x] adalah….
x 3
a. -6
b. 8
c. 12
d. 14
e. 16

11. Pembahasan 1:
Lim [6x-2x] = Lim 4x = 4(3) = 12
X 3 x 3
Pembahasan 2:
Lim [6x-2x] = Lim 6x – Lim 2x
X 3 x 3 x 3
= 6(3) – 2(3)
= 18 – 6 = 12
Limit fungsi aljabar

12. Hal.: 12 LIMIT FUNGSI
Limit fungsi bentuk
Jika f(x) = (x-a).h(x)
g(x) = (x-a).k(x)
Maka:
)
(
).
(
)
(
).
(
)
(
)
(
x
k
a
x
x
h
a
x
x
g
x
f
Lim
Lim a
x
a
x 




0
0
)
(
)
(
)
(
)
(
a
k
a
h
x
k
x
h
Lim
a
x

 
LIMIT FUNGSI ALJABAR

13. Hal.: 13 LIMIT FUNGSI
Limit Fungsi Bentuk
Jika diketahui limit tak hingga (~)
Sebagai berikut:
Maka:
1. R= 0 jika n<m
2. R= a jika n=m
3. R= ~ jika n>m
~
~
R
r
qx
px
c
bx
ax
m
m
n
n
x
Lim 








 ...
...
~
1
1
LIMIT FUNGSI ALJABAR

14. Hal.: 14 LIMIT FUNGSI
Limit Fungsi Bentuk (~ - ~)
a.
1. R= ~ jika a>p
2. R= 0 jika a=p
3. R= -~ jika a<p
  R
q
px
b
ax
Lim
x




~
LIMIT FUNGSI ALJABAR

15. Hal.: 15 LIMIT FUNGSI
b.
1. R= ~ jika a>p
2. jika a=p
3. R= -~ jika a<p
  R
r
qx
px
c
bx
ax
Lim
x







2
2
~
a
q
b
R
2


LIMIT FUNGSI ALJABAR

16. Hal.: 16 LIMIT FUNGSI
Soal latihan:
Nilai dari
adalah….
x
x
x
x
x
x
Lim
x 2
2
4
3
2
3
2
4
0 




LIMIT FUNGSI ALJABAR

17. Hal.: 17 LIMIT FUNGSI
Pembahasan:
Jika 0 didistribusikan menghasilkan ~
(bukan solusi) sehingga soal diselesaikan dengan
cara faktorisasi
0
0
0
.
2
0
0
.
2
0
.
4
0
.
3
0
2
2
4
3
2
3
2
4
2
3
2
4
0










 x
x
x
x
x
x
Lim
x
LIMIT FUNGSI ALJABAR

18. Hal.: 18 LIMIT FUNGSI
Maka:
 
 
2
2
4
2
0
0
4
0
0
2
2
4
3
2
2
4
3
2
2
4
3
2
3
0
2
3
0
2
3
2
4
0


























x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Lim
Lim
Lim
x
x
x
LIMIT FUNGSI ALJABAR

19. Hal.: 19 LIMIT FUNGSI
Nilai dari
adalah ….
1
8
2
6
3
4
2
2
~ 



 x
x
x
x
Lim
x

20. Hal.: 20 LIMIT FUNGSI
Pembahasan 1:
1
8
2
6
3
4
2
2
~ 



 x
x
x
x
Lim
x
2
2
2
2
2
2
2
2
2
2
1
8
2
6
3
4
1
8
2
6
3
4
x
x
x
x
x
x
x
x
x
x
x
x
x
x











21. Hal.: 21 LIMIT FUNGSI
Pembahasan 1:
0
0
2
0
0
4
~
1
~
8
2
~
6
~
3
4
2
2










2
2
4



22. Limit Fungsi Trigonometri
a
x 
1. Bentuk lim f(x) = f(a)
Contoh :
Tentukan nilai lim sin 2x.
4


x
Jawab :
Lim sin 2x = sin 2 = sin = 1






4

2

4


x

23. Hal.: 23 LIMIT FUNGSI
Limit Fungsi Trigonometri
2. Bentuk lim , dengan f(a) = 0 dan g(a) = 0
a
x 
 
 
x
g
x
f
Contoh :
Tentukan nilai dari :
x
x
cos
2
sin
lim
2


x
Jawab :
4


x
4


x
4


x
2
1
.
2
2
sin
2
sin
2
lim
cos
cos
sin
2
lim
cos
2
sin
lim 





x
x
x
x
x
x
x
x
x cos
sin
2
2
sin 
x
x 2
sin
2
1
2
cos 

Ingat !!!

24. Hal.: 24 LIMIT FUNGSI
Limit Fungsi Trigonometri
3. Bentuk atau
x
x
sin
lim
x
x
tan
lim
0

x 0

x
Catatan :
1.
2.
1
sin
lim
sin
lim 

x
x
x
x
1
tan
lim
tan
lim 

x
x
x
x
Secara umum
b
a
ax
ax
b
a
bx
ax
b
a
bx
ax



sin
tan
lim
,
tan
lim
,
sin
lim
0

x
0

x
0

x
0

x 0

x
0

x
0

x

26. Soal latihan
1. Nilai dari
adalah….
6
4
2
2
2 


 x
x
x
Lim
x
LIMITFUNGSIALJABAR

27. Limit FungsiTrigonometri
Contoh 1 :
Tentukan nilai limit fungsi trigonometri berikut!
x
x
a
x 2
8
sin
lim
.
0
 x
x
b
x 4
sin
3
tan
lim
.
0
