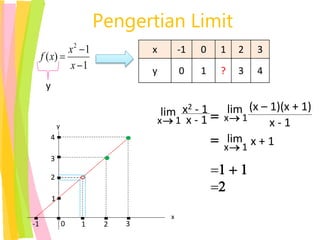
Dokumen ini membahas aspek-aspek limit fungsi aljabar, termasuk pengertian limit, metode penyelesaian, serta teorema-teorema yang terkait. Contoh-contoh disertakan untuk menjelaskan cara menentukan nilai limit, baik dari kanan maupun kiri, serta situasi di mana limit tidak ada. Selain itu, terdapat latihan soal yang dapat digunakan untuk menguji pemahaman tentang limit fungsi.

1. Sri Aji
Cakraningrum
Arita Jenni C
Argy Fadillah
Ezra M Fahrezy
Nafalia Nurjannah
Rinanda Erdika Putri
Kelompok 3
XI-MIA-1

2. Kompetensi Dasar
3.7 Menjelaskan limit fungsi aljabar (fungsi
polinom dan fungsi rasional) Secara intuitif
dan sifat - sifatnya, serta menentukan
eksistensinya.
4.7 Menyelesaikan masalah yang berkaitan
dengan limit fungsi aljabar

3. Limit Fungsi
Aljabar
Peta
Konsep
Limit
Fungsi
Teorema
Limit
Metode
Penyelesaian
Pengertian Limit
Limit fungsi yang tidak
memiliki nilai limit
Limit fungsi untuk
x →∞
Metode substitusi
Metode faktorisasi
Metode perkalian
bilangan sekawan
Menentukan nilai
Limit dengan
Aljabar
Bentuk tak tentu
Bentuk tak tentu
Bentuk tak tentu
dan
~
~  0
0
c
k

o
o
~
~

4. Pengertian Limit
Limit fungsi f(x) adalah suatu nilai yang didekati
oleh fungsi f(x) jika x mendekati suatu nilai tertentu.
Misal untuk x mendekati a maka f(x) mendekati L.
Istilah mendekati dinotasikan dengan “”
L
f(x)
lim
a
x
=

X mendekati a
fungsi
Nilai limit
Cara membaca :
Limit f(x) = L
untuk x mendekati a

5. Selidikilah nilai limit dari apabila x
mendekati 1.
• x mendekati 1 dari kiri :
…, -1, 0
• x mendekati 1 dari kanan :
2, 3, …
Nilai f(x) :
x -1 0 1 2 3
y 0 1 ? 3 4
1
1
)
(
2


=
x
x
x
f
Pengertian Limit

6. 1
1
)
(
2


=
x
x
x
f
y
x -1 0 1 2 3
y 0 1 ? 3 4
4
1
0 2 3
y
x
3
2
1
-1
x2 - 1
lim
1
x =
 x - 1
(x – 1)(x + 1)
lim
1
x
=
 x - 1
x + 1
lim
1
x
=1 + 1
=2

Pengertian Limit

7. Selidikilah nilai limit fungsi untuk x
mendekati 3.
• didekati dari kiri : f(x) = −∞
• didekati dari kanan : f(x) = ∞
Dari kiri Dari kanan
x fx) x f(x)
2
2,5
2,8
2,9
2,99
-1
-2
-5
-10
-100
4
3,5
3,8
3,1
3,01
1
2
1,25
10
100
3
1
)
(

=
x
x
f
Limit Fungsi Yang Tidak Memiliki
Nilai Limit

8. Dari tabel diatas , dapat disimpulkan bahwa
limit f(x) tidak ada untuk mendekati 3, atau secara
umum ditulis :
atau disebut :
Tidak ada untuk x mendekati 3
divergen untuk x mendekati 3
3
1
)
(

=
x
x
f
fungsi
1
lim =
3
x  3
Limit Fungsi Yang Tidak Memiliki
Nilai Limit

9. Selidikilah nilai limit fungsi untuk x
mendekati tak hingga.
Kesimpulan :
x f(x)
100
1.000
10.000
100.000
1.000.000
1,01
1,001
1,0001
1,00001
1,000001
*Semakin besar nilai x,
maka nilai f(x) akan
semakin dekat dengan 1
Limit Fungsi Untuk X →∞

10. Nilai Tentu Dalam Limit
k
b
a
=
0
0
=
k
~
0
=
k
~
~
~ =
+
~
k
(~) =
0
~
=
k
~
~
=
k
~
(~)
k =
K = bilangan asli = tak hingga
~
Keterangan :

11. Nilai Tidak Tentu
Dalam Limit
o
o
0
0
~
~ 
~
~
= tak hingga
~
Keterangan :

13. Teorema 1
k
k
lim
a
x
=

7
7
lim
8
x
=

Contoh :
5
5
lim
0
x
=

Teorema 2
a
x
lim
a
x
=

-2
x
lim
-2
x
=

Contoh :
0
x
lim
0
x
=

Teorema 3
kx
lim
a
x
=

Contoh :
k . a
x
k lim
a
x
=

3x
lim
-2
x
=

3 . (-2) = -6
x
3 lim
-2
x
=
 x
1
0
lim

x
=

Teorema 4
0
lim

x
=

Contoh :
n
x
k
0
lim

x
=
 2
7
x

14. Teorema 5
[f(x) + g(x)]
lim
a
x
=

Contoh :
f(x)
lim
a
x
g(x)
+ lim
a
x
[f(x) - g(x)]
lim
a
x
=

f(x)
lim
a
x
g(x)
- lim
a
x
[3x + 6]
lim
2
x
=

3x
lim
2
x
6
+ lim
2
x
x
3. lim
2
x
6
+ lim
2
x
=
= 3. 2 + 6
= 12
Contoh :
[4x -7]
lim
0
x
=

4x
lim
0
x
7
- lim
0
x
x
4. lim
0
x
7
- lim
0
x
=
= 4. 0 - 7
= -7

15. Teorema 6
[f(x) . g(x)]
lim
a
x
=

Contoh :
f(x)
lim
a
x
g(x)
. lim
a
x
x2
lim
2
x
=

x) .
(lim
2
x
=
Contoh :
[4x . 7x]
lim
1
x
=

4x
lim
1
x
7x
. lim
1
x
x
4. lim
1
x
x
. 7 lim
1
x
=
= (4 . 1) . (7 .1)
= 4.7
= 28
x . x
lim
2
x 
x)
(lim
2
x
= 2 . 2

16. Teorema 7
f(x)
lim
a
x =

f(x)
lim
a
x
g(x)
lim
a
x
g(x)
x - 1
lim
4
x =

(x – 1)
lim
4
x
(x – 3)
lim
4
x
x - 3
=
= 3
4 - 1
4 - 3
Contoh :
Teorema 8
[f(x)]n
lim
a
x
=

f(x) ]n
[lim
a
x 
[2x-1]3
lim
3
x
=

(2x-1)]3
[lim
3
x
= [2 . 3 – 1]3
= 53
= 125

17. Latihan
Soal

18. 21
lim
8
x
= ...

…
x
lim
14
x
=

6x
lim
4
x
= ...

…
lim

x
=
 2
7
x
[4x + 7]
lim
2
x
= ...

1.
2.
3.
4.
5.
[4x . 7x]
lim
8
x
= ...

6.
x - 5
lim
20
x = ...

[2x-2]3
lim
4
x
= ...

x – 15
7.
8.

19. Kunci Jawaban

20. 21
21
lim
8
x
=

14
x
lim
14
x
=

6x
lim
4
x
=

6 . 4 = 24
x
6 lim
4
x
=

0
lim

x
=
 2
7
x
[4x + 7]
lim
2
x
=

4x
lim
2
x
7
+ lim
2
x
1.
2.
3.
4.
5.
x
4. lim
2
x
7
+ lim
2
x
=
= 4. 2 + 7
= 56
x
4. lim
8
x
x
. 7 lim
8
x
=
= (4 . 8) . (7 .8)
= 32.56
= 1729
[4x . 7x]
lim
8
x
=

4x
lim
8
x
7x
. lim
8
x
6.

21. x - 5
lim
20
x =

(x – 5)
lim
20
x
(x – 15)
lim
20
x
[2x-2]3
lim
4
x
=

=
= 3
20-5
20-15
x – 15 = [2 . 4 – 2]3
= 63
= 216
(2x-2)]3
[lim
4
x
7. 8.

22. Menentukan nilai
limit dengan aljabar

23. MenentukanNilai Limit DenganAljabar
• Bentuktaktentu
0
0
Jikanilai x = a disubstitusilangsungke f(x)
padalim
𝑥→𝑎
𝑓 𝑥 ,diperolehbentuk
0
0
. Maka f(x) perludiubahbentuknya.
Contoh:
a. lim
𝑥→1
𝑥2
−1
𝑥2
−3𝑥+2
= …
Jikamensubstitusilangsungnilai x=1 maka:
• lim
𝑥→1
𝑥2
−1
𝑥2
−3𝑥+2
=
12
−1
12
−3.1+2
=
0
0
Agar bentukdapatditentukan, makadifaktorkan:
• lim
𝑥→1
𝑥2
−1
𝑥2
−3𝑥+2
= lim
𝑥→1
𝑥−1 𝑥+1
𝑥−1 𝑥−2
= lim
𝑥→1
𝑥+1
𝑥−2
=
1+1
1−2
= -2

24. Bentuk tak tentu
Limit f(x) untuk x ~ akan menghasilkan bentuk tak
tentu apabila x = ~ disubstitusi secara lagsung pada
fungsi pecahan polinom.
~
~
~
~
Pembagian suku-suku
pada pembilang dan
penyebut dengan x
berpangkat tertinggi
0
lim

x
=
 n
x
k
Penyelesaian :

25. 2
2
2
2
2
2
2
2
x
3
x
x
x
x
2
x
1
x
x
4
x
x
3
x
2
2
x
lim
3
x
x
2
1
x
4
x
3
lim
+


+
=
+


+




2
2
x
3
x
1
x
1
x
4
x 2
3
lim
+


+
=


2
3
0
0
2
0
0
3
+


+
=
=
Contoh :

26. 3
3
3
2
3
3
3
2
x
3
x
x
x
x
2
x
1
x
x
4
x
x
3
x
3
2
x
lim
6
4x
x
2
7
x
x
3
lim

+
+

=
+
+
+





3
3
x
6
x
4
x
7
x
1
x 2
3
lim

+
+

=


0
0
0
2
0
0
0
=
_
+
+

=
2
x
2

27. Tentukan nilai dari:
1.
= .
= =
Bentuk tak tentu & ~
~  0
0
c
k


28. Contoh soal

29. Contoh soal
a < p maka L = - ∞
a = p maka L =
1
2

30. Latihan
Soal

31. 1. ....
1
x
1
x
lim
2
1
x
=
+



1
x
)
1
x
)(
1
x
(
lim
1
x
1
x
lim
1
x
2
1
x +

+
=
+





)
1
x
(
lim1
x

= 

1
1 

=
2

=
2
1
x
1
x
lim
2
1
x

=
+




32. 2. ....
2
x
6
x
x
lim
2
2
x
=


+

2
x
)
3
x
)(
2
x
(
lim
2
x
6
x
x
lim
2
x
2
2
x 
+

=


+


)
3
x
(
lim
2
x
+
=

3
2+
=
5
=
5
2
x
6
x
x
lim
2
2
x
=


+


33. Rasionalka
n bentuk
akar
4
x
4
x
4
x
16
x
lim
4
x
16
x
lim
2
4
x
2
4
x 




=




3. ....
4
x
16
x
lim
2
4
x
=



4
x
4
x
)
16
x
(
lim
2
4
x 


=

4
x
4
x
)
4
x
)(
4
x
(
lim
4
x 


+
=

4
x
)
4
x
(
lim
4
x

+
=

4
4
)
4
4
( 
+
=
0
8 
=
0
=
0
4
x
16
x
lim
2
4
x
=




34. Kalikan akar
sekawan
x
1
x
1
x
1
x
1
x
x
1
x
1
lim
0
x 
+
+

+
+



+
=

)
x
1
x
1
(
x
x
2
lim
0
x 
+
+
=

4. ....
x
x
1
x
1
lim
0
x
=


+

....
x
x
1
x
1
lim
0
x
=


+

)
x
1
x
1
(
x
)
x
1
(
)
x
1
(
lim
0
x 
+
+


+
=

x
1
x
1
2
lim
0
x 
+
+
=

1
2
2
0
1
0
1
2
=
=

+
+
=
1
x
x
1
x
1
lim
0
x
=


+
