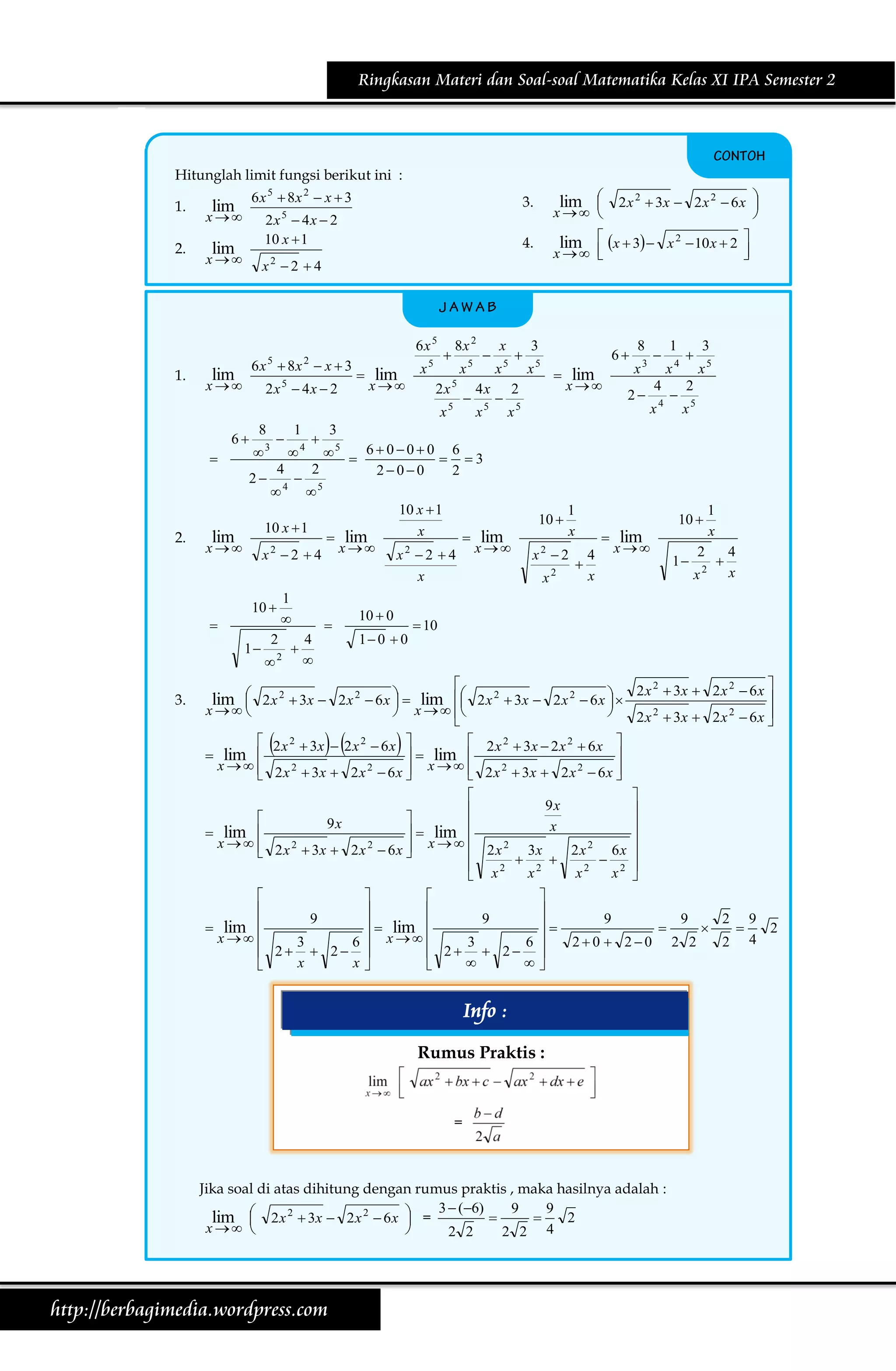
Dokumen ini membahas materi limit fungsi dan turunan dalam matematika kelas XI IPA semester 2. Penjelasan meliputi konsep limit di titik tertentu dan tak hingga, serta contoh perhitungan limit dan sifat-sifat fungsi aljabar. Terdapat juga langkah-langkah dalam menghitung limit fungsi dengan berbagai soal latihan.

1. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
6. Menggunakan konsep limit fungsi dan turunan
fungsi dalam pemecahan masalah.
6.1. Menjelaskan secara intuitif arti limit fungsi di
suatu titik dan di takhingga.
6.2. Menggunakan sifat limit fungsi untuk menghitung
bentuk tak tentu fungsi aljabar dan trigonometri
APERSEPSI
x2  x  2
x 1
Nilai fungsi tersebut untuk x = 1, adalah :
Diketahui fungsi : f ( x) 
12  1  2 0
  tak terdefinisi
1 1
0
Perhatikan nilai fungsi f ( x ) untuk x mendekati 1, sebagai berikut :
f (1) 
f(x)
Dalam hal ini dikatakan bahwa : limit fungsi f ( x ) untuk x
mendekati 1 dari kiri samadengan 3, dan dituliskan :’
lim

x 1
x2  x 3
3
x 1
x
tak terdefinisi
Jika nilai x mendekati 1 dari sebelah “kanan”, ternyata nilai
fungsi f ( x ) akan mendekati nilai 3.
Dalam hal ini dikatakan bahwa : limit fungsi f ( x ) untuk x
mendekati 1 dari kanan samadengan 3, dan dituliskan :’
lim

x 1
x2  x 3
3
x 1
f(x)
3
2
1,1
1,01
1,001
1,0001
1,00001
1,000001
1,0000001
5
4
3,1
3,01
3,001
3,0001
3,00001
3,000001
3,0000001
1
…
1
Jika nilai x mendekati 1 dari sebelah “kiri”, ternyata nilai
fungsi f ( x ) akan mendekati nilai 3.
…
2,5
2,7
2,9
2,99
2,999
2,9999
2,99999
2,999999
2,999999899
2,999999989
…
0,5
0,7
0,9
0,99
0,999
0,9999
0,99999
0,999999
0,9999999
0,99999999
…
x
tak terdefinisi
Kesimpulan :
Jika x mendekati 1 , maka nilai fungsi f ( x) 
lim
x 1
http://berbagimedia.wordpress.com
x2  x  2
akan mendekati 3, dituliskan :
x 1
x2  x 3
3
x 1

2. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
DEFINISI
lim f
xa
 x  k
, jika dan hanya jika , untuk x mendekati a , nilai f
 x  mendekati k
A . LIMIT FUNGSI ALJABAR UNTUK x → a
Jika f
 x  fungsi aljabar maka
lim f
xa
Langkah-langkah menghitung lim f
xa
 x  dinamakan limit fungsi aljabar .
 x  , jika
1.
Hitunglah nilai f  a  , jika f  a  
2.
 x  fungsi aljabar, adalah sebagai berikut :
f
Jika f  a  
0
, maka lim f
xa
0
 x  f a 
0
, maka f  x  harus disederhanakan terlebih dahulu .
0
Penyederhanaannya perlu memperhatikan bentuk f  x  , yaitu :
 Jika f
 Jika f
 x  merupakan persamaan aljabar biasa , maka f  x  difaktorkan terlebih dahulu
 x  merupakan bentuk akar , maka f  x  dikalikan dengan bentuk sekawannya
Hitunglah limit fungsi berikut ini :
1.
2.
1.
1
1
lim
x 3
x
3.
2
x2  6 x 8
x2
x2
x 3
Jadi
1
1
lim
x
1
lim
x 3
1
. Untuk x = 3 :
2
1
x
2

3.
x 6 x 8
. Untuk x = 2 :
x2
x2
4.

2x 1 1
1
1
3
2

1
1

9
8 2

9 3
2
0 C

0 0
x2  6 x  8 22  6. 2  8 0


x2
22
0
x  4x  2  lim x  4  2  4  2
x2  6 x 8
 lim
x2
x2
x2
x2
x2
2 x 2  7 x  15
x  5
x  4 x 5
2
x  5
x2  4 x 5
x
x0
2x 1 1
lim
x 0

. Untuk x = 2 :
2 x 2  7 x  15
lim
lim
Jadi
lim
x0
lim
lim
Jadi
2
x2  4 x 5
x
2
2
3
lim
Jadi
1
x
2
2.
x  5
4.
lim
2 x 2  7 x  15
lim

lim
x  5
. Untuk x = 0 :
x
x 0 

http://berbagimedia.wordpress.com

lim 
x  4 x 5
2


2  5 2  7 .  5   15
 5 
2 x  3x  5  lim
x  1x  5 x  5
0
2 . 0 1 1
x
x  0  2x  1 1


2x  1 1 
   lim 

x 0 
2x


2x  1 1
 x
lim 

2 x 2  7 x  15


0
0
2
 4 .  5   5

0
0
2 x  3 2  5   3 13


 5   1 6
x 1


2x  1 1 
2x  1  1
  lim  x
2x 1 1
2x 1 1  x  0 


2x  1  1 
2 . 0 1 1

1

2
2






3. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
Hitunglah limit fungsi berikut :
1.
x2  6 x
x 1
lim
x 8
9.
lim
x  2
2 x 2  9 x  10
x2
16.
lim
x  25
2 x  5 x  12
17.
lim
x 4
18.
lim
x 9
19.
lim
x 8
20.
lim
x 2
2
2.
lim
x4
x 2  2 x  11
x 1
10.
lim
x  4
3.
2 x2  x  3
lim
x 1 5  8 x  2 x 2
11.
2x 2  4 x  6
lim
x  1 2x 2  5 x  7
4.
lim
x2
x  9 x  14
x2
12.
5.
x 2  3 x  10
lim
x 5
x 5
2 x3
lim
2
3 4x  4 x  3
x
2
3x 2  8 x  4
13. lim
2
2
x   6 x  13 x  6
3
x 2  49
14. lim
x7 x 7
2
6.
7.
8.
lim
x  8
x2  2 x 8
x 2  5 x  24
x 8
x2  4 x 5
lim
x  1 x 2  8 x  9
x 3
lim
2
x  3 x  12 x  27
15.
lim
x  8
x  25
x 5
x4
x2  7 3
x 9
x 2  5x  6
x 2  4 x  32
x 2  6x  4
x 2  48 x  10
x 2  30 x  8
64  x 2
x 8
B . LIMIT FUNGSI ALJABAR UNTUK x → ∞
Teorema utama limit fungsi aljabar untuk x → ∞, adalah :
lim
x 
1
0
x
Ada dua bentuk limit fungsi aljabar untuk x   , yaitu :

Bentuk hasil bagi , yaitu lim
x
f x
, hasilnya dapat ditentukan dengan cara membagi sukugx
 x  dan g  x  dengan x yang pangkatnya paling tinggi .
Misal pangkat tertinggi dari f  x  adalah m dan pangkat tertinggi dari
suku f
maka :


Jika m  n , maka lim


Jika m  n , maka lim
Jika m  n , maka lim
x
x
x
g  x  adalah n ,
f x
koefisien pangkat tertinggi f x 
=
gx
koefisien pangkat tertinggi g x 
f x
= 
gx
f x
= 0
gx
Bentuk pengurangan , yaitu lim
x 
 f  x   g  x   , hasilnya dapat ditentukan dengan cara
f  x  g  x 
, sehingga diperoleh bentuk hasil bagi,
f  x  g  x 
kemudian tiap suku dari hasil dibagi dengan x yang pangkatnya paling tinggi.
mengalikan f  x   g  x  dengan
http://berbagimedia.wordpress.com

4. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
Hitunglah limit fungsi berikut ini :
1.
2.
3.
x 
2x  4x  2
10 x  1
lim
x 
x2  2  4
6 x  8x  x  3
5
lim
x
2
2x 5  4x  2

lim
x
x
5

6
8

1
8x 2
x
2x 5
x
5
5


x
x
4x
x
5

3

4

1
3.
2
2
x
x
2 x 2  3x  2 x 2  6 x 


6
5

8
x
lim
x
3
2
5
1

x
4
x
4
4


3
x5
2
x5
3

1

3
2


4


10  0
1 0  0
10 
1
x
x2  2
x2
x
10 

5
5  6  0  0  0  6  3
4
2
200
2
2 4  5


10 x  1
10 x  1
x
lim
 lim
 lim
x  x2  2  4 x  x2  2  4 x 

2.
lim  x  3  x 2  10 x  2 

x  


5
6x 5
1.
lim 

x  
4.
6 x 5  8x 2  x  3
lim
10 
4

x
 lim
x
1
2
x
2
1
x

4
x
 10

2 x 2  3x  2 x 2  6 x 

lim  2 x 2  3x  2 x 2  6 x   lim  2 x 2  3x  2 x 2  6 x  




x  



 

x   


2 x 2  3x  2 x 2  6 x 

 2 x 2  3x  2 x 2  6 x 
 2 x 2  3x  2 x 2  6 x 
  lim 

x    2 x 2  3x  2 x 2  6 x  x    2 x 2  3x  2 x 2  6 x 




lim 

 lim 
x 



 lim 
x 




9x



9x


x
  lim 

x
2
2
2
2
2 x  3x  2 x  6 x 
3x
2x
6x 
 2x

 2 
 2 

2
x
x2
x 
 x






9
9
9
9
2 9
  lim 




2
 x 

3
6
3
6
20  20 2 2
2 4
2  2 
 2  2 
x
x



Info :
Rumus Praktis :
=
Jika soal di atas dihitung dengan rumus praktis , maka hasilnya adalah :
3  (6)
9
9


2
lim  2 x 2  3x  2 x 2  6 x  =


x  

2 2
2 2 4
http://berbagimedia.wordpress.com

5. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
4.
lim  x  3  x 2  10 x  2 

x  


Jika akan dihitung dengan rumus praktis , maka bentuknya diubah menjadi :
lim  x  3  x 2  10 x  2   lim  x  32  x 2  10 x  2 

 x  
x  




 lim 
x  

Jadi :
x 2  6 x  9  x 2  10 x  2 


6  10  16
lim  x 2  6 x  9  x 2  10 x  2  

8


x  

2
2 1
Hitunglah limit fungsi berikut :
1.
2.
3x 4  x 2  6 x  1
lim
x   4  x 2  2x 3  6x 4
7.
lim
x
x 
8.
lim
x
9.
lim 

x  
10.
lim 4 x  2  16 x 2  3x  1

x  


11.
lim  9 x 2  x  2  3x  1

x  


12.
lim
x 
 6 x  5   3x 2  2 x  8 
lim
3
9x  4
8 x 4  2 x 3  3x  7
3.
lim
x   9 x 5  4 x 2  x  11
4.
lim
x 
5.
lim
x
6.
lim
x
x 6  3 x 5  x 3  10 x  16
7 x 3  2 x 2  12 x  3
12 x  3
4 x 2  16
7  14 x
x  3  6x
2
x2 8 x 9
6 x  11
8 x 2  23
9 x  42

4 x 2  12 x  3  4 x 2  6 x  1 


3x  18  5 x  12

C . TEOREMA-TEOREMA LIMIT FUNGSI
1.
2.
3.
4.
5.
lim C  C , dengan C = konstanta
xa
lim k f
 x 
lim  f
 x   g  x    lim f  x   lim g  x 
lim  f
 x  g  x    lim f  x  lim g  x 
xa
xa
x
k lim f
xa
, dengan k = konstanta
x a
xa
xa
xa
xa
lim f  x 
f  x  xa
lim

xa g  x 
lim g  x 
, jika lim g  x   0
xa
xa
6.
7.
http://berbagimedia.wordpress.com
lim
 f x
lim
n
xa
xa
f
n

  lim f
 xa
xn
lim f
xa
x


x
n

6. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
Hitunglah limit fungsi berikut dengan menerapkan teorema limit :

lim 
x4 







lim 2 x 3  1 4  x 2
x  1
1.

6x 5
lim  4 x  3
x2 
7x  6





1.

6x 5
lim  4 x  3

x2 
7x  6

lim 6 x 5
lim 6 x 5

x2
x2
  lim 4 x 
 4 lim x 
 x2
x2
lim 7 x 3  lim 6

lim  7 x 3  6 


x2
x2

x  2
2.
12  2 x
x5
3.


6  lim x 
x2 


6 lim x 5
x2
5
6 . 25
 4 lim x 
 4 lim x 
 4.2 
3
x2
x2
7 lim x 3  lim 6
7 . 23  6


x2
x2
 lim x   lim 6
7
x2  x2


 4.2 

lim 
x4 

12  2 x
x5

lim 
x4 

Jadi :
3.
7.2 6
3
 8
6 . 32
192 132
 8

7 .86
50
50

6x 5
lim  4 x  3
x2 
7x  6

Jadi :
2.
6 . 25

 132

 50

lim 12  lim 2 x
x4
x4

lim x  lim 5
x4
x4




12  2 x
x5
12  2 . 4

45
4 2

9 3
 2

 3



lim 12  2 lim x
x4
x4

lim x  lim 5
x4
x4



lim 2 x 3  1 4  x 2  lim 2 x 3  1  lim 4  x 2
x  1
x  1
x  1


 

  lim 2 x 3  lim 1   lim 4  lim x 2 
 x  1
x  1   x  1
x  1 

 

2

 

 
  2 lim x 3  lim 1   lim 4   lim x    2 13  1  4   12   1 3  3
 x  1
x  1   x  1  x  1  

 

 





lim 2 x 3  1 4  x 2   3
x  1
Jadi :
Hitunglah limit-limit fungsi berikut dengan menerapkan teorema limit :
1.


 1  x  3x  2 
lim 10 x  6 x  2 x  5
x  2

4
2
2.
lim 3x
x 1
3.
3
6
6
lim 4
x2 x 4
 5x 2  1 

lim  3
x 3  x  2 


4.

http://berbagimedia.wordpress.com


10
5.
lim 4 x 2  2
x  1
6.
 x2 

lim  3
x  3  4x  6 


7.
x2
lim 3 4
x  8 x  2x
8.
2 
 16 x
lim 


x  6  x 1 x  3 
3

7. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
D . LIMIT FUNGSI TRIGONOMETRI
Perhatikan lingkaran L dengan jari-jari 1
satuan.
Perhatikan sektor OBC :
1
1
LOBC  .OB.OC.x  (OB ) 2 x
2
2
1
2
 (cos x) . x
2
Perhatikan segitiga OBP :
1
1
LOBP  .OB.BP  cos x. sin x
2
2
Perhatikan sektor OAP :
1
1
1
LOAP  .OA.OP . x  .1.1. x  x
2
2
2
y
P ( cos x , sin x )
C
x
x
O
B
A(1,0)
LOBC  LOBP  LOAP
x 0
1
1
1
(cos x) 2 . x  cos x. sin x  x
2
2
2
(cos x) 2 . x cos x. sin x
x



x . cos x
x . cos x
x . cos x

 cos x 
sin x
1
 lim
x 0 x
x 0 cos x
 lim cos x  lim
 1  lim
x 0
sin x
1

x
cos x
sin x
1
x
Kesimpulan :
lim
x 0
sin x
1
x
E . TEOREMA LIMIT FUNGSI TRIGONOMETRI
lim
x0
sin x
1
x
,
lim
x 0
x
1
sin x
,
Hitunglah limit fungsi trigonometri berikut :
cos 2 x  3
lim
1.
cos x  1
1
x 
6x
lim
x  0 tan 2 x
3.
tan x
1
x
,
4.
lim
x0
5.
2
2.
lim
x0
lim
x2
lim
x0
x
1
tan x
1  cos 2 x
x2
x  4 tan x  2
x 2  6x  8
tan 4 x
lim
x  0 sin 3x
1.
lim
1
x 
cos 2 x  3
cos 2 x  3
1

, untuk x   diperoleh :
cos x  1
2
cos x  1
2
Jadi :
lim
1
x 
cos 2 x  3
 2
cos x  1
2
2.
3 . 2x
6x
2x
lim
 lim
 3 lim
 3 .1  3
x  0 tan 2 x x  0 tan 2 x
x  0 tan 2 x
http://berbagimedia.wordpress.com
1 
cos 2.    3
1  3
2 

 2
0 1
1 
cos     1
2 

8. Ringkasan Materi dan Soal-soal Matematika Kelas XI IPA Semester 2
3.
tan 4 x
4 x tan 4 x
3x
4 x tan 4 x
3x
lim
 lim

 lim


x  0 sin 3x x  0
4x
3x sin 3x x  0 3x
4x
sin 3x

4.
tan 4 x
4
3x
4
4
 lim
 lim
  1 1 
x  0 sin 3x 3
3 x  0 4x
3
lim
x 0
1  cos 2 x
 lim
x 0
x2
2 sin 2 x
x
2
 lim
x 0

1  1  2 sin 2 x
x2

lim
x 0
1  1  2 sin 2 x
x2
 lim
x 0
2 sin 2 x
x2
sin x
sin x
 sin x sin x 
 2 lim 

 lim
 2 .1.1  2
  2 lim
x 0  x
x 0 x
x 0 x
x 
Hitunglah limit-limit fungsi berikut :
1.
2


lim  sin x  cos x 
3
1

x  
2
2.
3.
4.
5.
sin x
lim
5
1

x   cos
6
4
sin 6 x
lim
x  0 2x
8 x
1
tan x
3
tan 4 x
lim
x  0 sin 3x
lim
x0
http://berbagimedia.wordpress.com
6.
lim
x 0
7.
lim
x 0
8.
1  cos x
x
1  cos x
x2
6x
lim
x  0 tan 2 x
9.
lim
x 0
10.
lim
x 0
cos ax  cos bx
x2
1  2 cos x  cos 2 x
x2