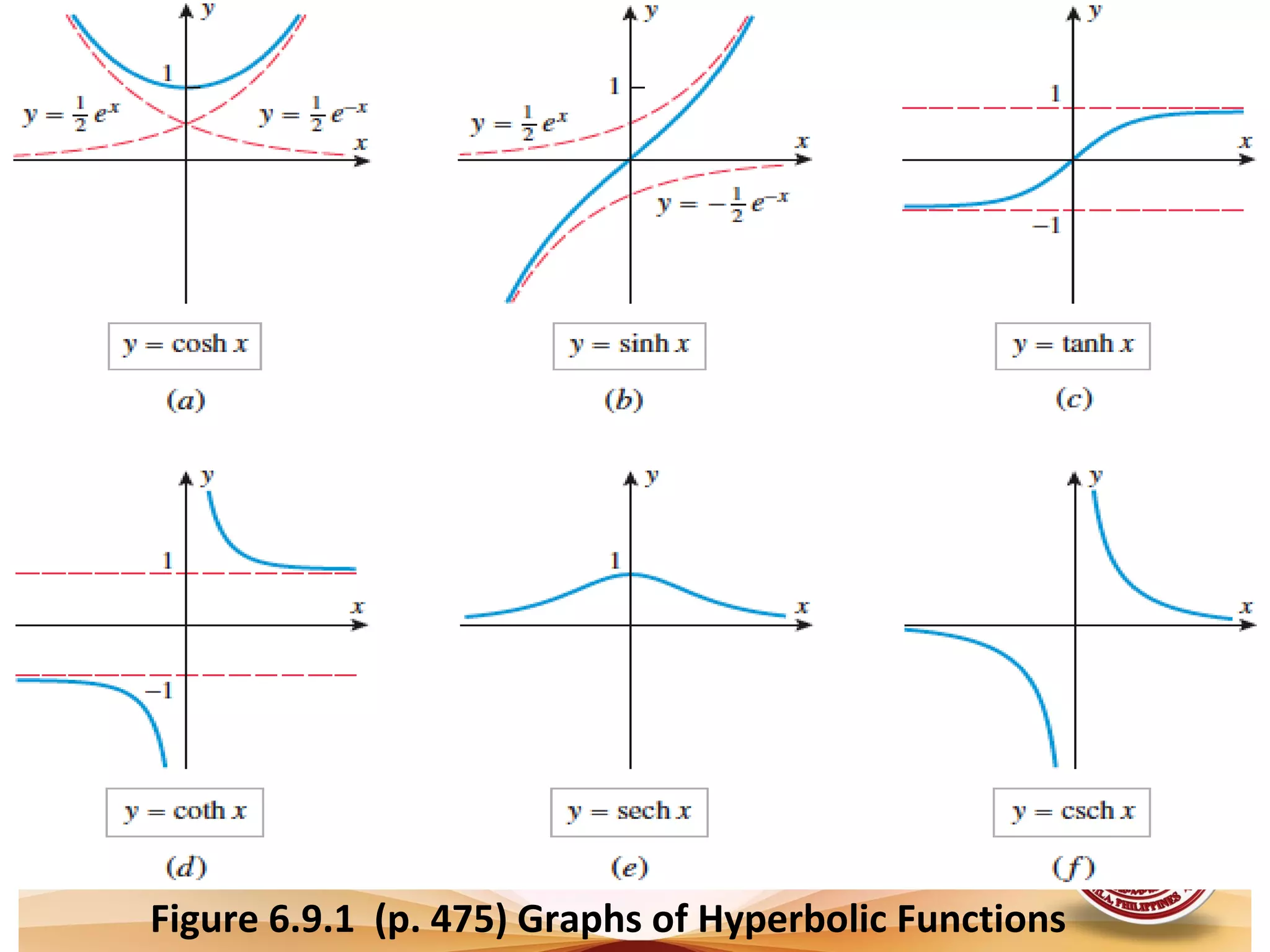
The document discusses differentiation of hyperbolic functions. It defines hyperbolic functions and their graphs, proves some identities and differentiation formulas, and gives examples of evaluating derivatives of hyperbolic functions. The key types of hyperbolic functions are defined as transcendental functions along with their inverses. Formulas are provided for taking the derivative of various hyperbolic functions. Examples are worked out and exercises given to evaluate derivatives of hyperbolic functions.

1. DIFFERENTIATION OF
HYPERBOLIC FUNCTIONS

2. OBJECTIVES:
• define and graph hyperbolic functions;
•prove some exercises on identities and
differentiation formulas;
•explain hyperbolic functions and their
derivatives; and
•evaluate problems on derivatives of
hyperbolic functions.

3. TRANSCENDENTAL FUNCTIONS
Kinds of transcendental functions:
1.logarithmic and exponential functions
2.trigonometric and inverse trigonometric
functions
3.hyperbolic and inverse hyperbolic functions
Note:
Each pair of functions above is an inverse to
each other.

4. Definition 6.9.1 (p. 474)

5. Figure 6.9.1 (p. 475) Graphs of Hyperbolic Functions

6. Theorem 6.9.2 (p. 476)
HYPERBOLIC IDENTITIES

7. Theorem 6.9.3 (p. 477)
DIFFERENTIATION FORMULA
Derivative of Hyperbolic Function

8. A. Find the derivative of each of the following functions
and simplify the result:
x2coshxsinhy.1 =
xcoshx2coshx2sinhxsinh2'y +=
xhsecxy.2 =
xhsec)xtanhxhsec(x'y +−=
xhsecy.3 2
=
xtanhxhsecxhsec2'y −=
xhsecxcothy.5 =
)xhcsc(xhsec)xtanhxhsec(xcoth'y 2
−+−=
2
xsinhlny.4 =
2
2
xsinh
xcoshx2
'y =
EXAMPLE:
)xtanhx1(xhsec'y −=
xtanhxhsec2'y 2
−=
2
xcothx2'y =
[ ]xhcscxtanhxcothxhsec'y 2
+−=
[ ]xhcsc1xhsec'y 2
+−=
xcothxhsec'y 2
−=

9. xcothlny.6 2
=
xcoth
xhcscxcoth2
'y 2
2
−
=
xcotharccosy.7 =
xcoth1
xhcsc
'y
2
2
−
−
−=
xhcscxhcsc
xhcscxhcsc
'y
22
22
−•−
−•
=
xsinh
xcosh
xsinh
1
2
'y
2
−
=
2
2
xsinhxcosh
2
'y •
−
=
x2sinh
4
'y −=
x2hcsc4'y −=
xhcsc
xhcsc
'y
2
2
−
=
xhcsc'y 2
−−=

10. )xharctan(siny.8 2
=
( )22
2
xcosh
xcoshx2
'y =
2
xhsecx2'y =
( )22
2
xsinh1
xcoshx2
'y
+
=

11. A. Find the derivative and simplify the result.
( ) 2
xsinhxf.1 =
( ) w4hsecwF.2 2
=
( ) 3
xtanhxG.3 =
( ) 3
tcoshtg.4 =
( )
x
1
cothxh.5 =
( ) ( )xtanhlnxg.6 =
EXERCISES:
( ) ( )ylncothyf.7 =
( ) xcoshexh.8 x
=
( ) ( )x2sinhtanxf.9 1−
=
( ) ( )x
xsinhxg.10 =
( ) ( )21
xtanhsinxg.11 −
=
( ) 0x,xxf.12 xsinh
>=