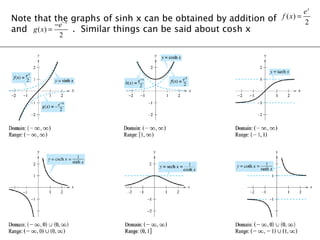
The document provides an overview of hyperbolic functions including: - Their properties, graphs, and relation to exponential functions - Differentiating and integrating hyperbolic functions - Properties of inverse hyperbolic functions - Examples of using hyperbolic functions to model hanging cables and finding derivatives and relative extrema.

1. Develop properties of hyperbolic functions Differentiate and integrate hyperbolic functions Develop properties of inverse hyperbolic functions Differentiate and integrate inverse hyperbolic functions Whew! Just a quick look at hyperbolic functions.

2. A brief look at hyperbolic functions: The name came from comparison of the area of semicircular regions with the area underneath a hyperbola.

3. Note that the graphs of sinh x can be obtained by addition of and . Similar things can be said about cosh x

5. Many of the trigonometric identities that you know and love have corresponding hyperbolic identities. In order to not mess with your head, I am not requiring you to memorize these for the test, but instead will provide you with a cheat sheet that will include definitions, graphs, identities, derivatives, integration, and like things for the inverse hyperbolic functions. Comparing to the trig identity cos 2 x + sin 2 x = 1,

6. Kind of mind blowing, the similarities. But remember, they are related to exponential growth and decay, e x and e -x .

7. The derivatives of sinh x and cosh x are written in terms of e x and e -x so their derivatives are easily found.

8. Ex 1 p391 Differentiation of Hyperbolic Functions product

9. Ex 2 p. 391 Finding Relative Extrema Find the relative extrema of f(x) = xsinh(x – 1) – cosh(x– 1) f ’(x) = xcosh(x – 1) + sinh(x – 1)(1) –-sinh(x –1) = xcosh(x – 1) f ‘(x)= 0 when x = 0 By the first derivative test, x = 0 gives a relative min, so (0, -cosh(-1)) is a relative minimum. Approximately (0, -1.543) Cosh, sinh, and tanh can be found in your catalog. The others must be defined using cosh, sinh, or tanh.

10. Ex 3 p. 391 Hanging Power Cables and Catenaries When a uniform flexible cable, such as a telephone wire, is suspended from two points that are at the same height, it takes the shape of a catenary . The way a necklace hangs is also a catenary. Power cables are suspended between two towers, forming the catenary shown in the figure. The equation for this catenary is y = a cosh (x/a) The distance between the two towers is 2b. Find the slope of the catenary at the point where the cable meets the right-hand tower. y‘=a sinh(x/a)*(1/a)=sinh(x/a). At the point where the cable meets the right-hand tower, x = b. So at the point (b, a cosh(b/a)), the slope (coming from the left) is m = sinh (b/a)

11. 5.8a p. 396/ 1-33 odd, 34, 37