Download as PDF, PPTX
![Piecewise-defined functions
Example
Let {
x2 0 ≤ x ≤ 1;
f(x) =
3−x 1 < x ≤ 2.
Find the domain and range of f and graph the function.
Solution
The domain is [0, 2]. The range is [0, 2). The graph is piecewise.
. .
2 .
. .
1 . .
. . .
0
. 1
. 2
.
. . . . . .](https://image.slidesharecdn.com/lesson01-functions027slides-090908144406-phpapp02/85/Lesson-1-Functions-14-320.jpg)
Uploaded byMatthew Leingang
Lesson 1: Functions
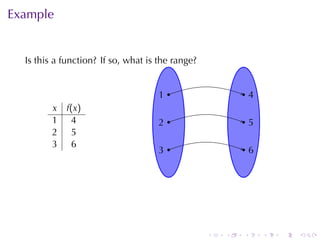
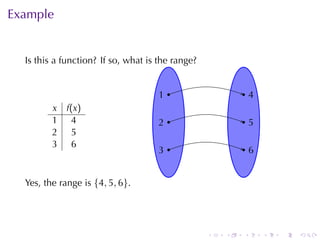
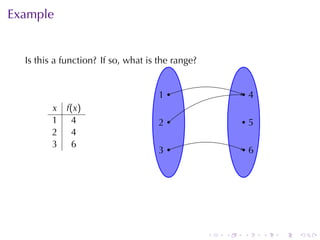
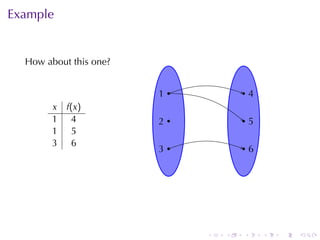
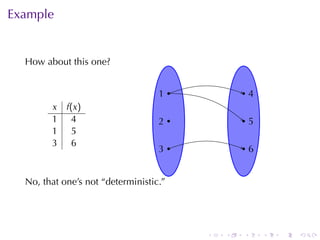
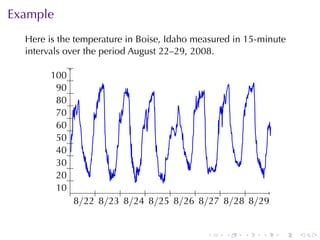
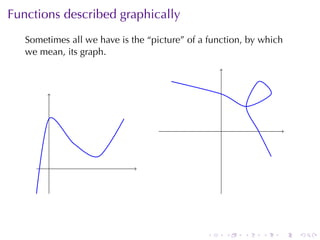
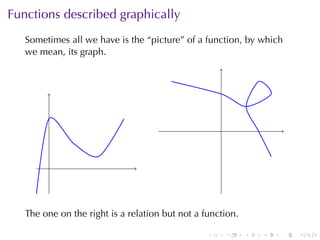
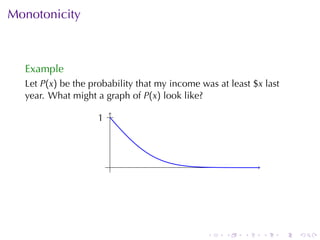
The document covers functions in calculus, defining a function as a relation assigning each element in a domain to a single element in a target set. It discusses various classes of functions including linear, polynomial, rational, trigonometric, and exponential functions, as well as properties such as monotonicity and how to express functions through formulas, graphs, and numerical data. Additionally, it provides examples and explanations of functions in real-world modeling contexts.
More Related Content
Lesson 1: Functions
- 1. Sections 1.1–1.2 Functions V63.0121, Calculus I September 10, 2009 Announcements Syllabus is on the common Blackboard Office Hours TBA . . . . . .
- 2. Outline What is a function? Modeling Examples of functions Functions expressed by formulas Functions described numerically Functions described graphically Functions described verbally Properties of functions Monotonicity Classes of Functions Linear functions Other Polynomial functions Other power functions Rational functions Trigonometric Functions Exponential and Logarithmic functions . . . . . .
- 3. Definition A function fis a relation which assigns to to every element x in a set D a single element f(x) in a set E. The set D is called the domain of f. The set E is called the target of f. The set { f(x) | x ∈ D } is called the range of f. . . . . . .
- 4. Outline What is a function? Modeling Examples of functions Functions expressed by formulas Functions described numerically Functions described graphically Functions described verbally Properties of functions Monotonicity Classes of Functions Linear functions Other Polynomial functions Other power functions Rational functions Trigonometric Functions Exponential and Logarithmic functions . . . . . .
- 5. The Modeling Process . . Real-world . . m . odel Mathematical . Problems Model s . olve .est t . i .nterpret . Real-world . Mathematical . Predictions Conclusions . . . . . .
- 6. Plato’s Cave . . . . . .
- 7. The Modeling Process . . Real-world . . m . odel Mathematical . Problems Model s . olve .est t . i .nterpret . Real-world . Mathematical . Predictions Conclusions S . hadows F . orms . . . . . .
- 8. Outline What is a function? Modeling Examples of functions Functions expressed by formulas Functions described numerically Functions described graphically Functions described verbally Properties of functions Monotonicity Classes of Functions Linear functions Other Polynomial functions Other power functions Rational functions Trigonometric Functions Exponential and Logarithmic functions . . . . . .
- 9. Functions expressed by formulas Any expression in a single variable x defines a function. In this case, the domain is understood to be the largest set of x which after substitution, give a real number. . . . . . .
- 10. Example x+1 Let f(x) = . Find the domain and range of f. x−1 . . . . . .
- 11. Example x+1 Let f(x) = . Find the domain and range of f. x−1 Solution The denominator is zero when x = 1, so the domain is all real numbers excepting one. As for the range, we can solve x+1 y+1 y= =⇒ x = x−1 y−1 So as long as y ̸= 1, there is an x associated to y. . . . . . .
- 12. No-no’s for expressions Cannot have zero in the denominator of an expression Cannot have a negative number under an even root (e.g., square root) Cannot have the logarithm of a negative number . . . . . .
- 13. Piecewise-defined functions Example Let { x2 0 ≤ x ≤ 1; f(x) = 3−x 1 < x ≤ 2. Find the domain and range of f and graph the function. . . . . . .
- 14. Piecewise-defined functions Example Let { x2 0 ≤ x ≤ 1; f(x) = 3−x 1 < x ≤ 2. Find the domain and range of f and graph the function. Solution The domain is [0, 2]. The range is [0, 2). The graph is piecewise. . . 2 . . . 1 . . . . . 0 . 1 . 2 . . . . . . .
- 15. Functions described numerically We can just describe a function by a table of values, or a diagram. . . . . . .
- 16. Example Is this a function?If so, what is the range? x f(x) 1 4 2 5 3 6 . . . . . .
- 17. Example Is this a function?If so, what is the range? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 2 5 3 6 . . 3 .. 6 . . . . . .
- 18. Example Is this a function?If so, what is the range? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 2 5 3 6 . . 3 .. 6 Yes, the range is {4, 5, 6}. . . . . . .
- 19. Example Is this a function?If so, what is the range? x f(x) 1 4 2 4 3 6 . . . . . .
- 20. Example Is this a function?If so, what is the range? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 2 4 3 6 . . 3 .. 6 . . . . . .
- 21. Example Is this a function?If so, what is the range? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 2 4 3 6 . . 3 .. 6 Yes, the range is {4, 6}. . . . . . .
- 22. Example How about this one? x f(x) 1 4 1 5 3 6 . . . . . .
- 23. Example How about this one? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 1 5 3 6 . . 3 .. 6 . . . . . .
- 24. Example How about this one? . . 1 .. 4 x f(x) 1 4 . .. 2 .. . 5 1 5 3 6 . . 3 .. 6 No, that one’s not “deterministic.” . . . . . .
- 25. In science, functions are often defined by data. Or,we observe data and assume that it’s close to some nice continuous function. . . . . . .
- 26. Example Here is the temperature in Boise,Idaho measured in 15-minute intervals over the period August 22–29, 2008. . 1 . 00 . 9 .0. 8 .0. 7 .0. 6 .0. 5 .0. 4 .0. 3 .0. 2 .0. 1 .0. . . . . . . . 8 . /22 . /23 . /24 . /25 . /26 . /27 . /28 . /29 8 8 8 8 8 8 8 . . . . . .
- 27. Functions described graphically Sometimes all we have is the “picture” of a function, by which we mean, its graph. . . . . . . . .
- 28. Functions described graphically Sometimes all we have is the “picture” of a function, by which we mean, its graph. . . The one on the right is a relation but not a function. . . . . . .
- 29. Functions described verbally Oftentimes our functions come out of nature and have verbal descriptions: The temperature T(t) in this room at time t. The elevation h(θ) of the point on the equation at longitude θ. The utility u(x) I derive by consuming x burritos. . . . . . .
- 30. Outline What is a function? Modeling Examples of functions Functions expressed by formulas Functions described numerically Functions described graphically Functions described verbally Properties of functions Monotonicity Classes of Functions Linear functions Other Polynomial functions Other power functions Rational functions Trigonometric Functions Exponential and Logarithmic functions . . . . . .
- 31. Monotonicity Example Let P(x) be the probability that my income was at least $x last year. What might a graph of P(x) look like? . . . . . .
- 32. Monotonicity Example Let P(x) be the probability that my income was at least $x last year. What might a graph of P(x) look like? . . 1 . . . . . . .
- 33. Monotonicity Definition A function f is decreasing if f(x1 ) > f(x2 ) whenever x1 < x2 for any two points x1 and x2 in the domain of f. A function f is increasing if f(x1 ) < f(x2 ) whenever x1 < x2 for any two points x1 and x2 in the domain of f. . . . . . .
- 34. Examples Example Going back to the burrito function, would you call it increasing? . . . . . .
- 35. Examples Example Going back to the burrito function, would you call it increasing? Example Obviously, the temperature in Boise is neither increasing nor decreasing. . . . . . .
- 36. Outline What is a function? Modeling Examples of functions Functions expressed by formulas Functions described numerically Functions described graphically Functions described verbally Properties of functions Monotonicity Classes of Functions Linear functions Other Polynomial functions Other power functions Rational functions Trigonometric Functions Exponential and Logarithmic functions . . . . . .
- 37. Classes of Functions linear functions, defined by slope an intercept, point and point, or point and slope. quadratic functions, cubic functions, power functions, polynomials rational functions trigonometric functions exponential/logarithmic functions . . . . . .
- 38. Linear functions Linear functions have a constant rate of growth and are of the form f(x) = mx + b. . . . . . .
- 39. Linear functions Linear functions have a constant rate of growth and are of the form f(x) = mx + b. Example In New York City taxis cost $2.50 to get in and $0.40 per 1/5 mile. Write the fare f(x) as a function of distance x traveled. . . . . . .
- 40. Linear functions Linear functions have a constant rate of growth and are of the form f(x) = mx + b. Example In New York City taxis cost $2.50 to get in and $0.40 per 1/5 mile. Write the fare f(x) as a function of distance x traveled. Answer If x is in miles and f(x) in dollars, f(x) = 2.5 + 2x . . . . . .
- 41. Other Polynomial functions Quadratic functions take the form f(x) = ax2 + bx + c The graph is a parabola which opens upward if a > 0, downward if a < 0. . . . . . .
- 42. Other Polynomial functions Quadratic functions take the form f(x) = ax2 + bx + c The graph is a parabola which opens upward if a > 0, downward if a < 0. Cubic functions take the form f(x) = ax3 + bx2 + cx + d . . . . . .
- 43. Other power functions Whole number powers: f(x) = xn . 1 negative powers are reciprocals: x−3 = 3 . x √ fractional powers are roots: x1/3 = 3 x. . . . . . .
- 44. Rational functions Definition A rational function is a quotient of polynomials. Example x 3 (x + 3 ) The function f(x) = is rational. (x + 2)(x − 1) . . . . . .
- 45. Trigonometric Functions Sine and cosine Tangent and cotangent Secant and cosecant . . . . . .
- 46. Exponential and Logarithmic functions exponential functions (for example f(x) = 2x ) logarithmic functions are their inverses (for example f(x) = log2 (x)) . . . . . .