The document provides detailed guidelines for solving optimization problems, including methods such as the closed interval method, first and second derivative tests, and examples on minimizing functions under constraints. It also discusses specific mathematical problems, such as finding dimensions of areas in a triangle and maximizing profits in an economics scenario with a focus on functions and their critical points. Various methods for analysis, including calculus concepts, are outlined to aid in problem-solving.

1. Section 4.5
Optimization II
V63.0121.034, Calculus I
November 25, 2009
Announcements
Final Exam, December 18, 2:00–3:50pm
. . . . . .

2. Outline
Recall
More examples
Addition
Distance
Triangles
Economics
The Statue of Liberty
. . . . . .

3. Checklist for optimization problems
1. Understand the Problem What is known? What is
unknown? What are the conditions?
2. Draw a diagram
3. Introduce Notation
4. Express the “objective function” Q in terms of the other
symbols
5. If Q is a function of more than one “decision variable”, use
the given information to eliminate all but one of them.
6. Find the absolute maximum (or minimum, depending on the
problem) of the function on its domain.
. . . . . .

4. Recall: The Closed Interval Method
See Section 4.1
To find the extreme values of a function f on [a, b], we need to:
Evaluate f at the endpoints a and b
Evaluate f at the critical points x where either f′ (x) = 0 or f is
not differentiable at x.
The points with the largest function value are the global
maximum points
The points with the smallest or most negative function value
are the global minimum points.
. . . . . .

5. Recall: The First Derivative Test
See Section 4.3
Theorem (The First Derivative Test)
Let f be a continuous function and c a critical point of f in (a, b).
If f′ (x) > 0 on (a, c) (i.e., “before c”) and f′ (x) < 0 on (c, b)
(i.e., “after c”, then c is a local maximum for f.
If f′ (x) < 0 on (a, c) and f′ (x) > 0 on (c, b), then c is a local
minimum for f.
If f′ (x) has the same sign on (a, c) and (c, b), then c is not a
local extremum.
. . . . . .

6. Recall: The Second Derivative Test
See Section 4.3
Theorem (The Second Derivative Test)
Let f, f′ , and f′′ be continuous. Let c be be a point in (a, b) with
f′ (c) = 0.
If f′′ (c) < 0, then f(c) is a local maximum.
If f′′ (c) > 0, then f(c) is a local minimum.
If f′′ (c) = 0, the second derivative test is inconclusive (this does
not mean c is neither; we just don’t know yet).
. . . . . .

7. Which to use when? The bottom line
Use CIM if it applies: the domain is a closed, bounded
interval
If domain is not closed or not bounded, use 2DT if you like
to take derivatives, or 1DT if you like to compare signs.
. . . . . .

8. Outline
Recall
More examples
Addition
Distance
Triangles
Economics
The Statue of Liberty
. . . . . .

9. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
. . . . . .

10. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
Solution
Objective: minimize S = x + y subject to the constraint that
xy = 16
. . . . . .

11. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
Solution
Objective: minimize S = x + y subject to the constraint that
xy = 16
Eliminate y: y = 16/x so S = x + 16/x. The domain of
consideration is (0, ∞).
. . . . . .

12. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
Solution
Objective: minimize S = x + y subject to the constraint that
xy = 16
Eliminate y: y = 16/x so S = x + 16/x. The domain of
consideration is (0, ∞).
Find the critical points: S′ (x) = 1 − 16/x2 , which is 0 when
x = 4.
. . . . . .

13. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
Solution
Objective: minimize S = x + y subject to the constraint that
xy = 16
Eliminate y: y = 16/x so S = x + 16/x. The domain of
consideration is (0, ∞).
Find the critical points: S′ (x) = 1 − 16/x2 , which is 0 when
x = 4.
Classify the critical points: S′′ (x) = 32/x3 , which is always
positive. So the graph is always concave up, 4 is a local min,
and therefore the global min.
. . . . . .

14. Addition with a constraint
Example
Find two positive numbers x and y with xy = 16 and x + y as
small as possible.
Solution
Objective: minimize S = x + y subject to the constraint that
xy = 16
Eliminate y: y = 16/x so S = x + 16/x. The domain of
consideration is (0, ∞).
Find the critical points: S′ (x) = 1 − 16/x2 , which is 0 when
x = 4.
Classify the critical points: S′′ (x) = 32/x3 , which is always
positive. So the graph is always concave up, 4 is a local min,
and therefore the global min.
So the numbers are x = y = 4, Smin = 8.
. . . . . .

15. Distance
Example
Find the point P on the parabola y = x2 closest to the point (3, 0).
. . . . . .

16. Distance
Example
Find the point P on the parabola y = x2 closest to the point (3, 0).
Solution y
.
. x, x2 )
(
.
. . x
.
3
.
. . . . . .

17. Distance
Example
Find the point P on the parabola y = x2 closest to the point (3, 0).
Solution y
.
The distance between (x, x2 )
and (3, 0) is given by
√
f(x) = (x − 3)2 + (x2 − 0)2
. x, x2 )
(
.
. . x
.
3
.
. . . . . .

18. Distance
Example
Find the point P on the parabola y = x2 closest to the point (3, 0).
Solution y
.
The distance between (x, x2 )
and (3, 0) is given by
√
f(x) = (x − 3)2 + (x2 − 0)2
We may instead minimize
the square of f:
g(x) = f(x)2 = (x − 3)2 + x4 . x, x2 )
(
.
. . x
.
3
.
. . . . . .

19. Distance
Example
Find the point P on the parabola y = x2 closest to the point (3, 0).
Solution y
.
The distance between (x, x2 )
and (3, 0) is given by
√
f(x) = (x − 3)2 + (x2 − 0)2
We may instead minimize
the square of f:
g(x) = f(x)2 = (x − 3)2 + x4 . x, x2 )
(
.
. . x
.
The domain is (−∞, ∞).
3
.
. . . . . .

20. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
. . . . . .

21. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
g′ (x) = 2(x − 3) + 4x3 = 4x3 + 2x − 6 = 2(2x3 + x − 3)
. . . . . .

22. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
g′ (x) = 2(x − 3) + 4x3 = 4x3 + 2x − 6 = 2(2x3 + x − 3)
If a polynomial has integer roots, they are factors of the
constant term (Euler)
. . . . . .

23. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
g′ (x) = 2(x − 3) + 4x3 = 4x3 + 2x − 6 = 2(2x3 + x − 3)
If a polynomial has integer roots, they are factors of the
constant term (Euler)
1 is a root, so 2x3 + x − 3 is divisible by x − 1:
f′ (x) = 2(2x3 + x − 3) = 2(x − 1)(2x2 + 2x + 3)
The quadratic has no real roots (the discriminant
b2 − 4ac < 0)
. . . . . .

24. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
g′ (x) = 2(x − 3) + 4x3 = 4x3 + 2x − 6 = 2(2x3 + x − 3)
If a polynomial has integer roots, they are factors of the
constant term (Euler)
1 is a root, so 2x3 + x − 3 is divisible by x − 1:
f′ (x) = 2(2x3 + x − 3) = 2(x − 1)(2x2 + 2x + 3)
The quadratic has no real roots (the discriminant
b2 − 4ac < 0)
We see f′ (1) = 0, f′ (x) < 0 if x < 1, and f′ (x) > 0 if x > 1. So
1 is the global minimum.
. . . . . .

25. Distance problem
minimization step
We want to find the global minimum of g(x) = (x − 3)2 + x4 .
g′ (x) = 2(x − 3) + 4x3 = 4x3 + 2x − 6 = 2(2x3 + x − 3)
If a polynomial has integer roots, they are factors of the
constant term (Euler)
1 is a root, so 2x3 + x − 3 is divisible by x − 1:
f′ (x) = 2(2x3 + x − 3) = 2(x − 1)(2x2 + 2x + 3)
The quadratic has no real roots (the discriminant
b2 − 4ac < 0)
We see f′ (1) = 0, f′ (x) < 0 if x < 1, and f′ (x) > 0 if x > 1. So
1 is the global minimum.
The point on the parabola closest to (3, 0) is (1, 1). The
√
minimum distance is 5.
. . . . . .

26. Remark
We’ve used each of the methods (CIM, 1DT, 2DT) so far.
Notice how we argued that the critical points were absolute
extremes even though 1DT and 2DT only tell you
relative/local extremes.
. . . . . .

27. A problem with a triangle
Example
Find the rectangle of maximal area inscribed in a 3-4-5 right
triangle as shown.
Solution
5
.
4
.
.
3
.
. . . . . .

28. A problem with a triangle
Example
Find the rectangle of maximal area inscribed in a 3-4-5 right
triangle as shown.
Solution
Let the dimensions of
the rectangle be x and y.
5
. x
.
4
.
y
.
.
3
.
. . . . . .

29. A problem with a triangle
Example
Find the rectangle of maximal area inscribed in a 3-4-5 right
triangle as shown.
Solution
Let the dimensions of
the rectangle be x and y.
Similar triangles give
y 4 5
. x
.
= =⇒ 3y = 4(3−x) 4
.
3−x 3
y
.
.
3
.
. . . . . .

30. A problem with a triangle
Example
Find the rectangle of maximal area inscribed in a 3-4-5 right
triangle as shown.
Solution
Let the dimensions of
the rectangle be x and y.
Similar triangles give
y 4 5
. x
.
= =⇒ 3y = 4(3−x) 4
.
3−x 3
4 y
.
So y = 4 − x and
3
( ) .
4 4 3
.
A(x) = x 4 − x = 4x− x2
3 3
. . . . . .

31. Triangle Problem
maximization step
4 2
We want to find the absolute maximum of A(x) = 4x − x on
3
the interval [0, 3].
. . . . . .

32. Triangle Problem
maximization step
4 2
We want to find the absolute maximum of A(x) = 4x − x on
3
the interval [0, 3].
A(0) = A(3) = 0
. . . . . .

33. Triangle Problem
maximization step
4 2
We want to find the absolute maximum of A(x) = 4x − x on
3
the interval [0, 3].
A(0) = A(3) = 0
8 12
A′ (x) = 4 − x, which is zero when x = = 1.5.
3 8
. . . . . .

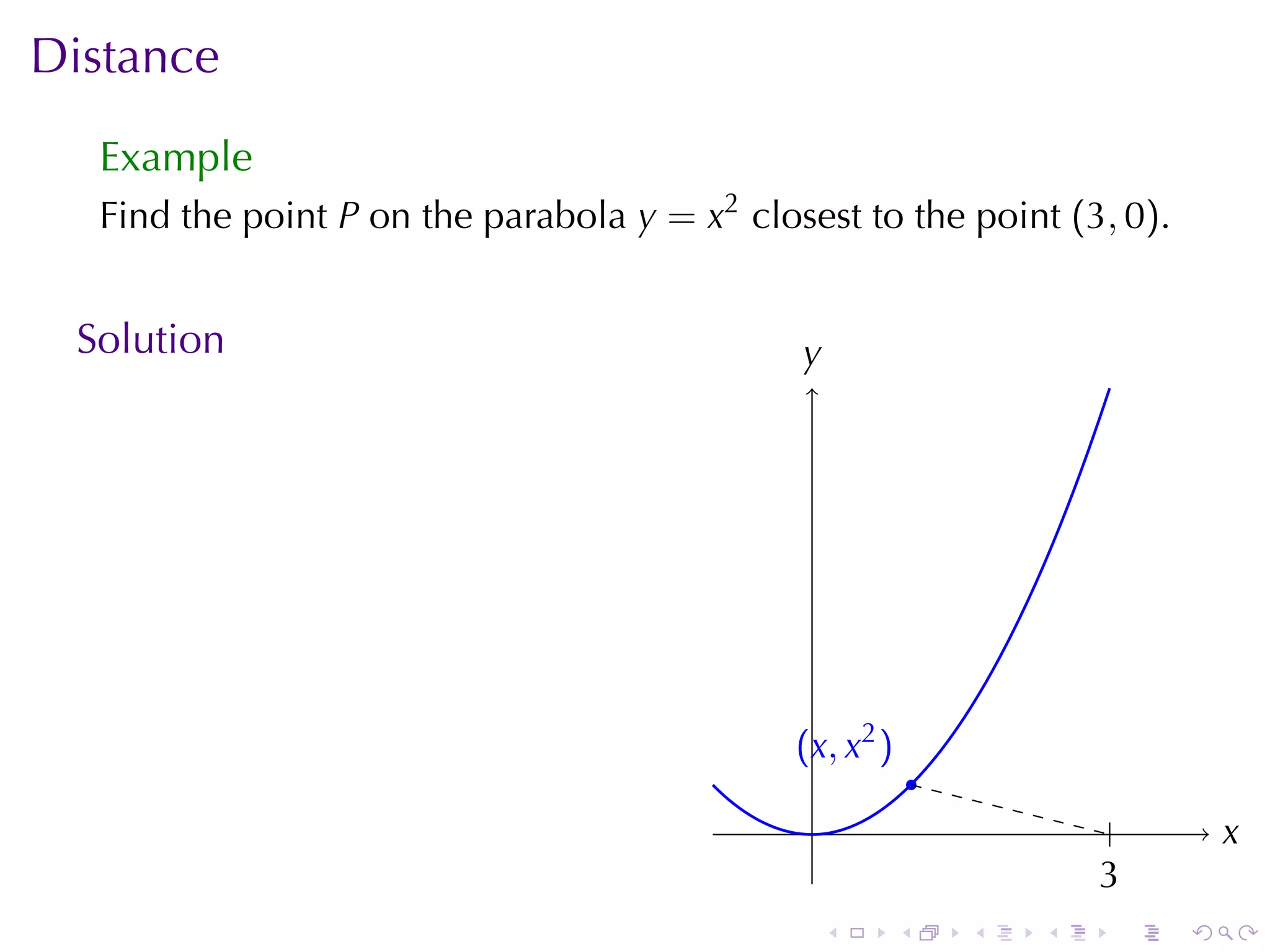
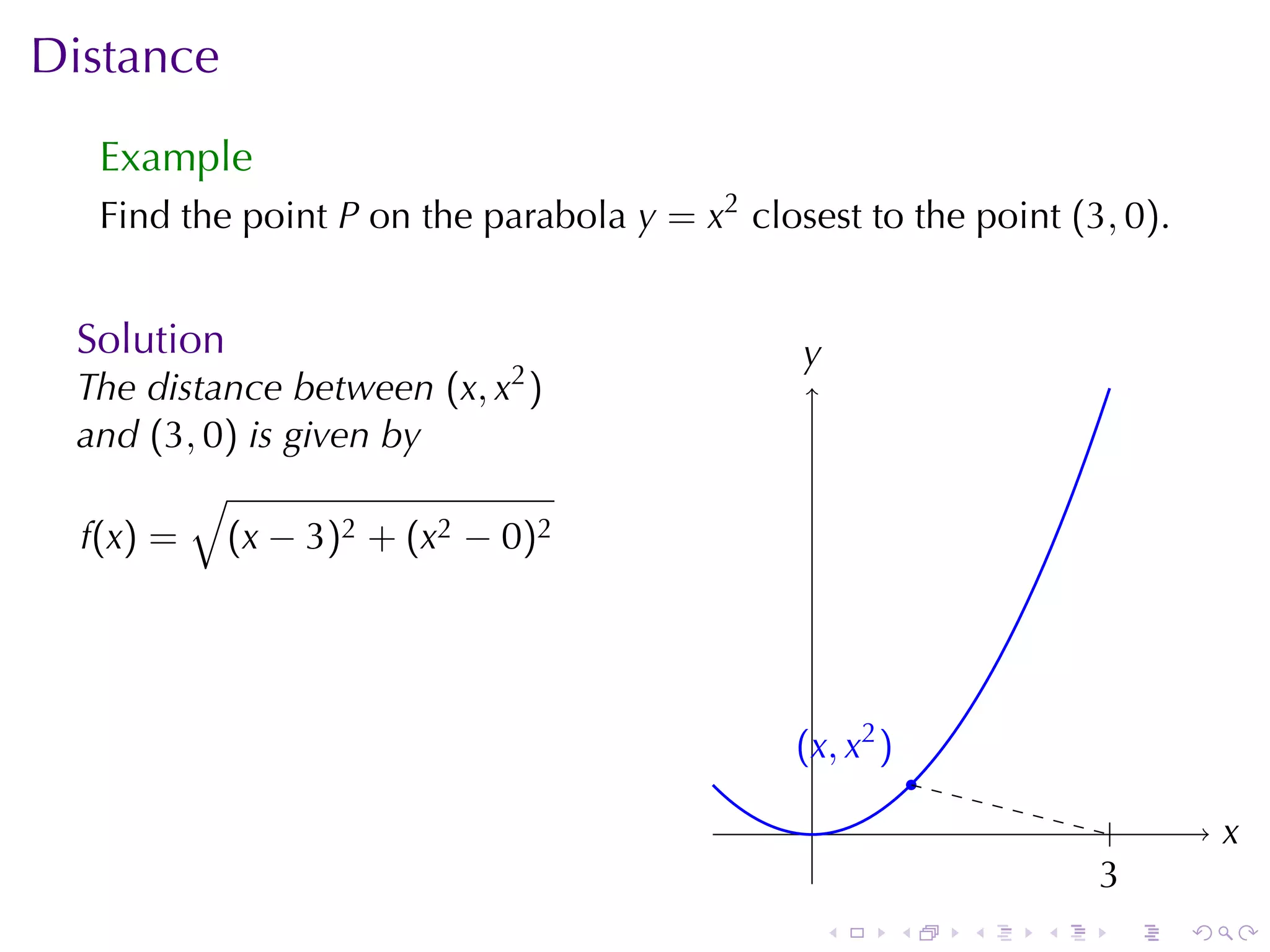
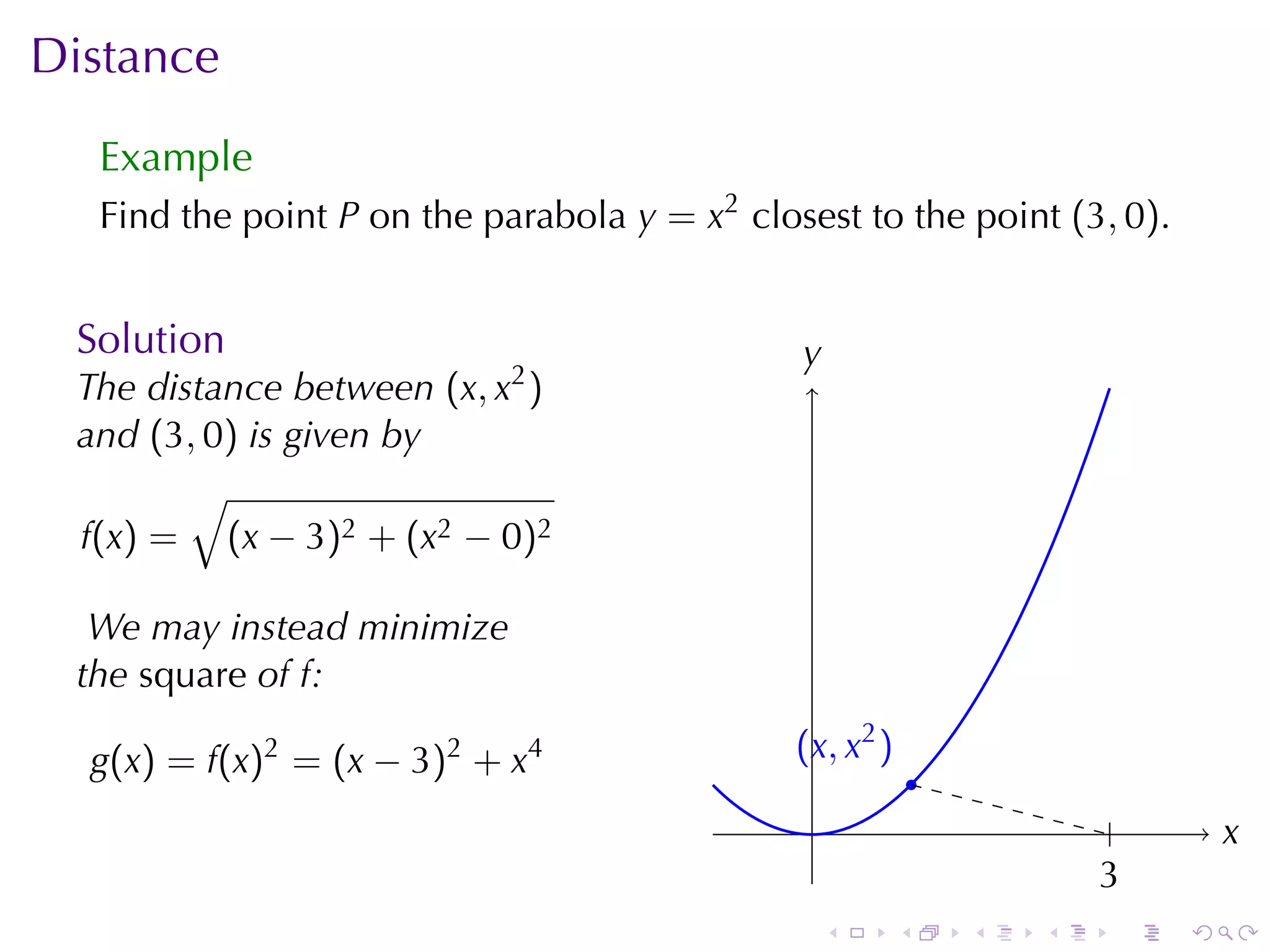
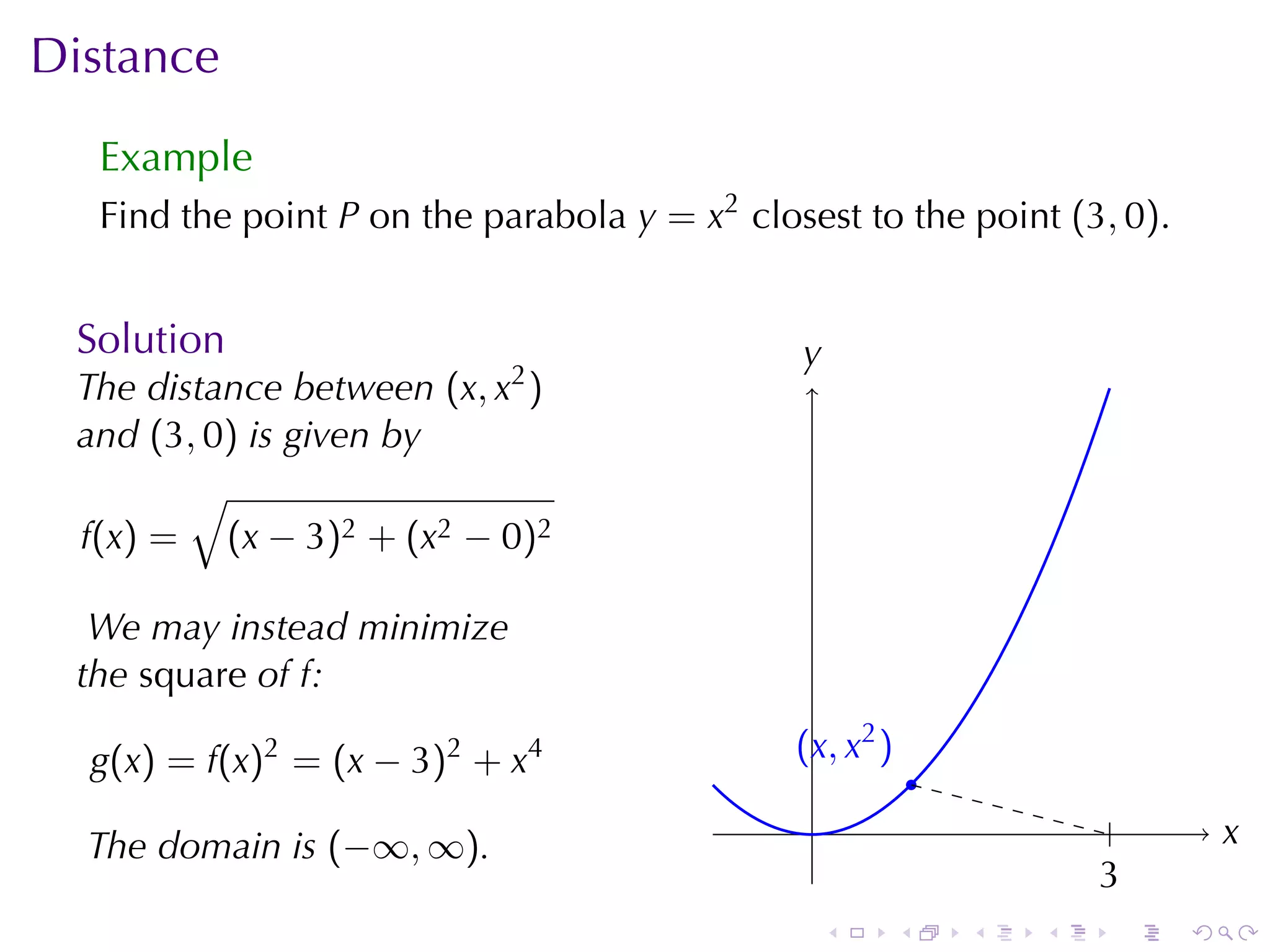
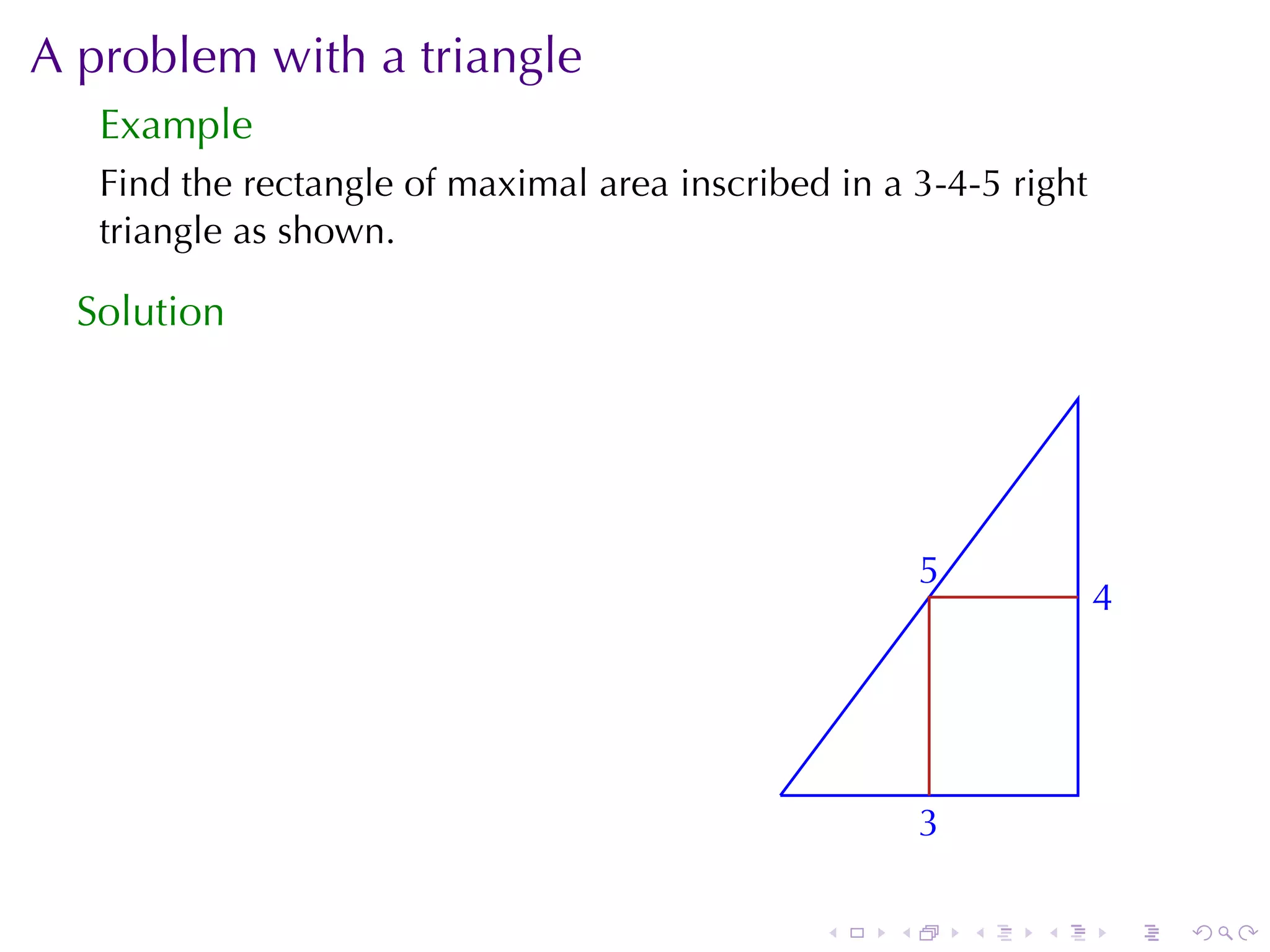
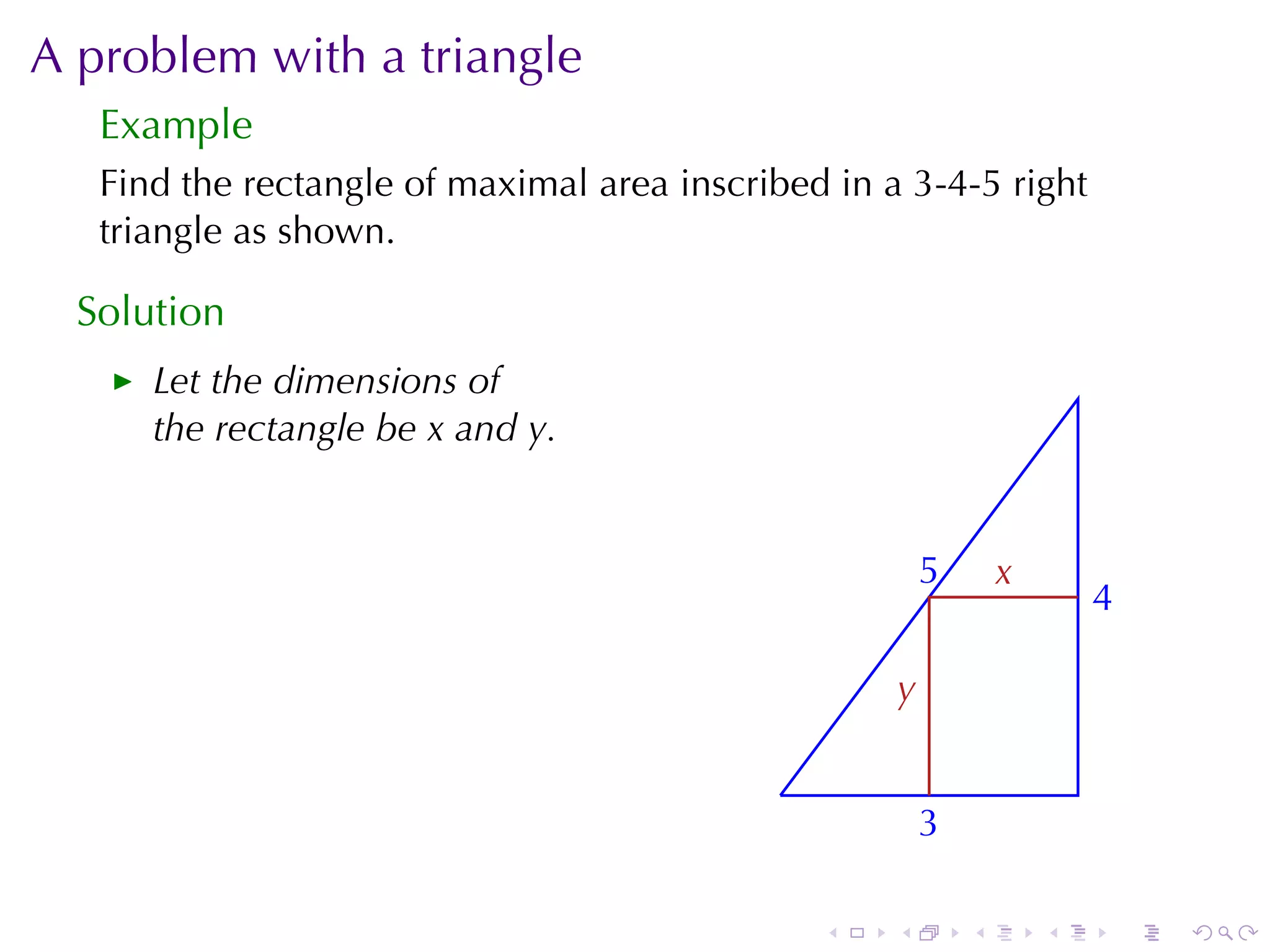
34. Triangle Problem
maximization step
4 2
We want to find the absolute maximum of A(x) = 4x − x on
3
the interval [0, 3].
A(0) = A(3) = 0
8 12
A′ (x) = 4 − x, which is zero when x = = 1.5.
3 8
Since A(1.5) = 3, this is the absolute maximum.
. . . . . .

35. Triangle Problem
maximization step
4 2
We want to find the absolute maximum of A(x) = 4x − x on
3
the interval [0, 3].
A(0) = A(3) = 0
8 12
A′ (x) = 4 − x, which is zero when x = = 1.5.
3 8
Since A(1.5) = 3, this is the absolute maximum.
So the dimensions of the rectangle of maximal area are
1.5 × 2.
. . . . . .

36. An Economics problem
Example
Let r be the monthly rent per unit in an apartment building with
100 units. A survey reveals that all units can be rented when
r = 900 and that one unit becomes vacant with each 10 increase
in rent. Suppose the average monthly maintenance costs per
occupied unit is $100/month. What rent should be charged to
maximize profit?
. . . . . .

37. An Economics problem
Example
Let r be the monthly rent per unit in an apartment building with
100 units. A survey reveals that all units can be rented when
r = 900 and that one unit becomes vacant with each 10 increase
in rent. Suppose the average monthly maintenance costs per
occupied unit is $100/month. What rent should be charged to
maximize profit?
Solution
Let n be the number of units rented, depending on price (the
demand function).
∆n 1
We have n(900) = 100 and = − . So
∆r 10
1 1
n − 100 = − (r − 900) =⇒ n(r) = − r + 190
10 10
. . . . . .

38. Economics Problem
Finishing the model and maximizing
The profit per unit rented is r − 100, so
( )
1
P(r) = (r − 100)n(r) = (r − 100) − r + 190
10
1 2
= − r + 200r − 19000
10
. . . . . .

39. Economics Problem
Finishing the model and maximizing
The profit per unit rented is r − 100, so
( )
1
P(r) = (r − 100)n(r) = (r − 100) − r + 190
10
1 2
= − r + 200r − 19000
10
We want to maximize P on the interval 900 ≤ r ≤ 1900.
. . . . . .

40. Economics Problem
Finishing the model and maximizing
The profit per unit rented is r − 100, so
( )
1
P(r) = (r − 100)n(r) = (r − 100) − r + 190
10
1 2
= − r + 200r − 19000
10
We want to maximize P on the interval 900 ≤ r ≤ 1900.
A(900) = $800 × 100 = $80, 000, A(1900) = 0
. . . . . .

41. Economics Problem
Finishing the model and maximizing
The profit per unit rented is r − 100, so
( )
1
P(r) = (r − 100)n(r) = (r − 100) − r + 190
10
1 2
= − r + 200r − 19000
10
We want to maximize P on the interval 900 ≤ r ≤ 1900.
A(900) = $800 × 100 = $80, 000, A(1900) = 0
1
A′ (x) = − r + 200, which is zero when r = 1000.
5
. . . . . .

42. Economics Problem
Finishing the model and maximizing
The profit per unit rented is r − 100, so
( )
1
P(r) = (r − 100)n(r) = (r − 100) − r + 190
10
1 2
= − r + 200r − 19000
10
We want to maximize P on the interval 900 ≤ r ≤ 1900.
A(900) = $800 × 100 = $80, 000, A(1900) = 0
1
A′ (x) = − r + 200, which is zero when r = 1000.
5
n(1000) = 90, so P(r) = $900 × 90 = $81, 000. This is the
maximum intake.
. . . . . .

43. The Statue of Liberty
The Statue of Liberty stands on top of a pedestal which is on top
of on old fort. The top of the pedestal is 47 m above ground level.
The statue itself measures 46 m from the top of the pedestal to the
tip of the torch.
What distance should one stand away from the statue in order to
maximize the view of the statue? That is, what distance will
maximize the portion of the viewer’s vision taken up by the
statue?
. . . . . .

44. The Statue of Liberty
Seting up the model
The angle subtended by the
statue in the viewer’s eye can a
be expressed as
( ) ( ) b
a+b b θ
θ = arctan −arctan .
x x
x
The domain of θ is all positive real numbers x.
. . . . . .

45. The Statue of Liberty
Finding the derivative
( ) ( )
a+b b
θ = arctan − arctan
x x
So
dθ 1 −(a + b) 1 −b
= ( )2 · − ( )2 · 2
dx a+b x2 b x
1+ x 1+ x
b a+b
= 2
−
x2 +b x2
+ (a + b ) 2
[ 2 ] [ ]
x + (a + b)2 b − (a + b) x2 + b2
=
(x2 + b2 ) [x2 + (a + b)2 ]
. . . . . .

46. The Statue of Liberty
Finding the critical points
[ ] [ ]
dθ x2 + (a + b)2 b − (a + b) x2 + b2
=
dx (x2 + b2 ) [x2 + (a + b)2 ]
. . . . . .

47. The Statue of Liberty
Finding the critical points
[ ] [ ]
dθ x2 + (a + b)2 b − (a + b) x2 + b2
=
dx (x2 + b2 ) [x2 + (a + b)2 ]
This derivative is zero if and only if the numerator is zero, so
we seek x such that
[ ] [ ]
0 = x2 + (a + b)2 b − (a + b) x2 + b2 = a(ab + b2 − x2 )
. . . . . .

48. The Statue of Liberty
Finding the critical points
[ ] [ ]
dθ x2 + (a + b)2 b − (a + b) x2 + b2
=
dx (x2 + b2 ) [x2 + (a + b)2 ]
This derivative is zero if and only if the numerator is zero, so
we seek x such that
[ ] [ ]
0 = x2 + (a + b)2 b − (a + b) x2 + b2 = a(ab + b2 − x2 )
√
The only positive solution is x = b(a + b).
. . . . . .

49. The Statue of Liberty
Finding the critical points
[ ] [ ]
dθ x2 + (a + b)2 b − (a + b) x2 + b2
=
dx (x2 + b2 ) [x2 + (a + b)2 ]
This derivative is zero if and only if the numerator is zero, so
we seek x such that
[ ] [ ]
0 = x2 + (a + b)2 b − (a + b) x2 + b2 = a(ab + b2 − x2 )
√
The only positive solution is x = b(a + b).
Using the first derivative test, we see that dθ/dx > 0 if
√ √
0 < x < b(a + b) and dθ/dx < 0 if x > b(a + b).
So this is definitely the absolute maximum on (0, ∞).
. . . . . .

50. The Statue of Liberty
Final answer
If we substitute in the numerical dimensions given, we have
√
x = (46)(93) ≈ 66.1 meters
This distance would put you pretty close to the front of the old
fort which lies at the base of the island.
Unfortunately, you’re not allowed to walk on this part of the lawn.
. . . . . .

51. The Statue of Liberty
Discussion
√
The length b(a + b) is the geometric mean of the two
distances measured from the ground—to the top of the
pedestal (a) and the top of the statue (a + b).
The geometric mean is of two numbers is always between
them and greater than or equal to their average.
. . . . . .