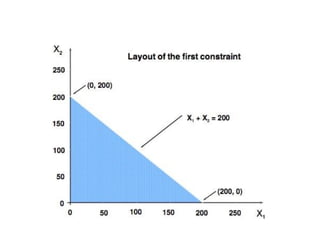
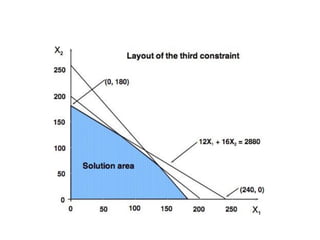
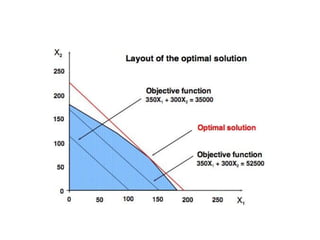
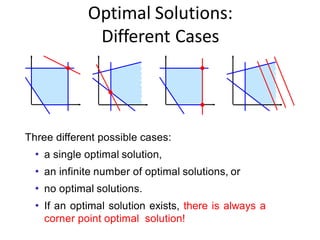
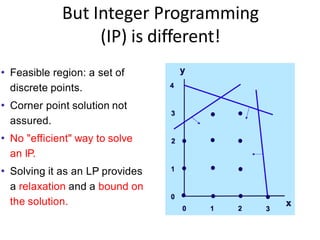
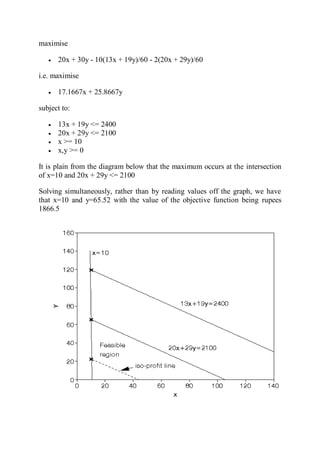
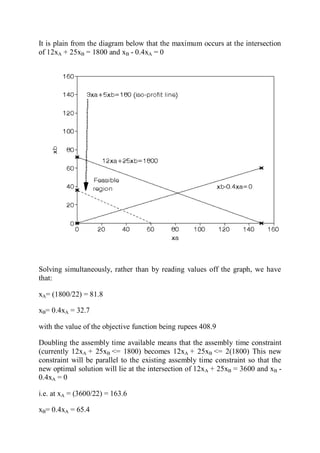
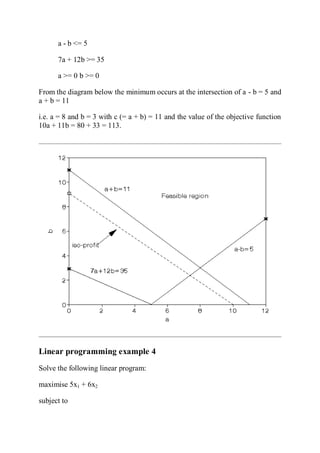
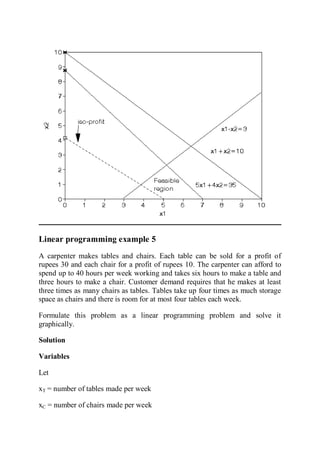
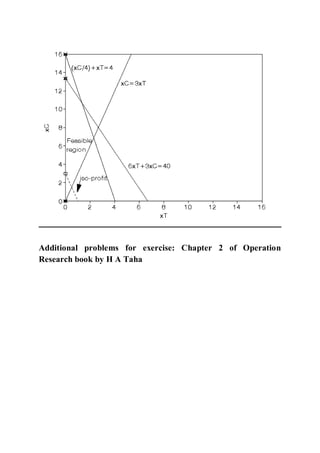
This document provides an introduction to linear programming. It defines linear programming as an optimization problem that involves maximizing or minimizing a linear objective function subject to linear constraints. Various terminology used in linear programming like decision variables, objective function, and constraints are explained. Several examples of linear programming problems from areas like production planning, scheduling, and resource allocation are presented and formulated mathematically. Graphical and algebraic solution methods for linear programming problems are discussed. The document also notes that integer programming problems cannot be solved using the same techniques as linear programs due to the discrete nature of the variables. Additional linear programming examples and problems from an operations research textbook are listed for further practice.

1. UNIT 3
Linear Programming - Introduction
Dr. Kailash Chaudhary
Ph.D. (Mechanical Design), M.E. (P & I), B.E. (Mechanical Engg)
Assistant Professor
Department of Mechanical Engineering
MBM Engineering College
ME 342 A
System Design and Analysis

2. Lecture Contents
Introduction to optimization
Modelling and Solving simple problems
Modelling combinatorial problems.
Duality or Assessing the quality of a solution.

3. Motivation
Why linear programming is a very important topic?
• A lot of problems can be formulated as linear
programmes
• There exist efficient methods to solve them
• or at least give good approximations.
• Solve difficult problems: e.g. original example given
by the inventor of the theory, Dantzig. Best
assignment of 70 people to 70 tasks.

4. What is a linear programme?
• Optimization problem consisting in
• Maximizing (or minimizing) a linear objective
function
• of n decision variables
• subject to a set of constraints expressed by
linear equations or inequalities.
• Terminology due to George B. Dantzig, inventor of
the Simplex Algorithm (1947)

5. Terminology
max 350x1 + 300x2
subject to
x1 + x2 ≤200
9x1 + 6x2 ≤1566
12x1 + 16x2 ≤2880
x1, x2 ≥0
x1,x2 : Decision variables
Objective function
Constraints

6. Terminology
max 350x1 + 300x2
subject to
x1 + x2 ≤200
9x1 + 6x2 ≤1566
12x1 + 16x2 ≤2880
x1, x2 ≥0
x1,x2 : Decision variables
Objective function
Constraints
In linear programme: objective function + constraints
are all linear
Typically (not always): variables are non-negative
If variables are integer: system called Integer
Programme (IP)

7. Terminology
xj ≥ 0 for all 1 ≤j ≤n.
• the problem is a maximization;
• all constraints are inequalities (and not equations);
• all variables are non-negative.
Linear programmes can be written under the standard form:
∑n
j=1 cjxj
Maximize
Subject to: ∑n
j=1 aijxj ≤ bi for all 1 ≤i ≤m (1)

8. Example 1: a resource allocation
problem
A company produces copper cable of 5 and 10 mm of diameter on a
single production line with the following constraints:
• The available copper allows to produces 21000 meters of cable of
5 mm diameter per week.
• A meter of 10 mm diameter copper consumes 4 times more
copper than a meter of 5 mm diameter copper.
Due to demand, the weekly production of 5 mm cable is limited to
15000 meters and the production of 10 mm cable should not exceed
40% of the total production. Cable are respectively sold 50 and 200
euros the meter.
What should the company produce in order to maximize its weekly
revenue?

9. Define two decision variables:
• x1: the number of thousands of meters of 5 mm cables produced
every week
• x2: the number of thousands meters of 10 mm cables produced
every week
The revenue associated to a production (x1,x2) is
z = 50x1 + 200x2.
The capacity of production cannot be exceeded
x1 + 4x2 ≤21.

10. The demand constraints have to be satisfied
2
4
10
x ≤ ( 1 2
x + x )
x1 ≤15
Negative quantities cannot be produced
x1 ≥0,x2 ≥0.

11. The model: To maximize the sell revenue, determine the solutions of
the following linear programme x1 and x2:
max z = 50x1 + 200x2
subject to
x1 + 4x2 ≤21
−4x1 + 6x2 ≤0
x1 ≤15
x1,x2 ≥0

12. Example 2: Scheduling
• m = 3 machines
• n = 8 tasks
• Each task lasts x units of
time
Objective: affect the tasks to the machines in order to minimize the
duration
• Here, the 8 tasks are finished after 7 units of times on 3
machines.

13. • m = 3 machines
• n = 8 tasks
• Each task lasts x units of
time
Objective: affect the tasks to the machines in order to minimize the
duration
• Now, the 8 tasks are accomplished after 6.5 units of time

14. Graphical Method
• The constraints of a linear programme define a
zone of solutions.
• The best point of the zone corresponds to the
optimal solution.
• For problem with 2 variables, easy to draw the
zone of solutions and to find the optimal solution
graphically.

15. Graphical Method
Example:
max 350x1 +300x2
subject to
x1 + x2 ≤200
9x1 + 6x2 ≤1566
12x1 + 16x2 ≤2880
x1, x2 ≥0

22. Computation of optimal solution
The optimal solution is at the intersection of the constraints:
x1 + x2 = 200 (2)
9x1 + 6x2 = 1566 (3)
We get:
x1 = 122
x2 = 78
Objective = 66100.

23. Optimal Solutions:
Different Cases
Three different possible cases:
• a single optimal solution,
• an infinite number of optimal solutions, or
• no optimal solutions.
• If an optimal solution exists, there is always a
corner point optimal solution!

24. Solving Linear Programmes

25. Solving Linear Programmes
• The constraints of an LP give rise to a geometrical shape:
a polyhedron
• If we can determine all the corner points of the polyhedron, then
we calculate the objective function at these points and take the
best one as our optimal solution.
• The Simplex Method intelligently moves from corner to corner
until it can prove that it has found the optimal solution.

26. Solving Linear Programmes
• Geometric method impossible in higher dimensions
• Algebraical methods:
• Simplex method (George B. Dantzig 1949):
skim through the feasible solution polytope.
Similar to a "Gaussian elimination".
Very good in practice, but can take an
exponential time.

27. But Integer Programming
(IP) is different!
• Feasible region: a set of
discrete points.
• Corner point solution not
assured.
• No "efficient" way to solve
an IP.
• Solving it as an LP provides
a relaxation and a bound on
the solution.

28. Linear programming example 1
A company is involved in the production of two items (X and Y). The resources
need to produce X and Y are twofold, namely machine time for automatic
processing and craftsman time for hand finishing. The table below gives the
number of minutes required for each item:
Machine time Craftsman time
Item X 13 20
Y 19 29
The company has 40 hours of machine time available in the next working week
but only 35 hours of craftsman time. Machine time is costed at rupees10 per
hour worked and craftsman time is costed at rupees 2 per hour worked. Both
machine and craftsman idle times incur no costs. The revenue received for each
item produced (all production is sold) is rupees 20 for X and rupees 30 for Y.
The company has a specific contract to produce 10 items of X per week for a
particular customer.
 Formulate the problem of deciding how much to produce per week as a
linear program.
 Solve this linear program graphically.
Solution
Let
 x be the number of items of X
 y be the number of items of Y
then the LP is:
maximise
 20x + 30y - 10(machine time worked) - 2(craftsman time worked)
subject to:
 13x + 19y <= 40(60) machine time
 20x + 29y <= 35(60) craftsman time
 x >= 10 contract
 x,y >= 0
so that the objective function becomes

29. maximise
 20x + 30y - 10(13x + 19y)/60 - 2(20x + 29y)/60
i.e. maximise
 17.1667x + 25.8667y
subject to:
 13x + 19y <= 2400
 20x + 29y <= 2100
 x >= 10
 x,y >= 0
It is plain from the diagram below that the maximum occurs at the intersection
of x=10 and 20x + 29y <= 2100
Solving simultaneously, rather than by reading values off the graph, we have
that x=10 and y=65.52 with the value of the objective function being rupees
1866.5

30. Linear programming example 2
A company manufactures two products (A and B) and the profit per unit sold is
rupees 3 and rupees 5 respectively. Each product has to be assembled on a
particular machine, each unit of product A taking 12 minutes of assembly time
and each unit of product B 25 minutes of assembly time. The company
estimates that the machine used for assembly has an effective working week of
only 30 hours (due to maintenance/breakdown).
Technological constraints mean that for every five units of product A produced
at least two units of product B must be produced.
 Formulate the problem of how much of each product to produce as a
linear program.
 Solve this linear program graphically.
 The company has been offered the chance to hire an extra machine,
thereby doubling the effective assembly time available. What is
the maximum amount you would be prepared to pay (per week) for the
hire of this machine and why?
Solution
Let
xA = number of units of A produced
xB = number of units of B produced
then the constraints are:
12xA + 25xB <= 30(60) (assembly time)
xB >= 2(xA/5)
i.e. xB - 0.4xA >= 0
i.e. 5xB >= 2xA (technological)
where xA, xB >= 0
and the objective is
maximise 3xA + 5xB

31. It is plain from the diagram below that the maximum occurs at the intersection
of 12xA + 25xB = 1800 and xB - 0.4xA = 0
Solving simultaneously, rather than by reading values off the graph, we have
that:
xA= (1800/22) = 81.8
xB= 0.4xA = 32.7
with the value of the objective function being rupees 408.9
Doubling the assembly time available means that the assembly time constraint
(currently 12xA + 25xB <= 1800) becomes 12xA + 25xB <= 2(1800) This new
constraint will be parallel to the existing assembly time constraint so that the
new optimal solution will lie at the intersection of 12xA + 25xB = 3600 and xB -
0.4xA = 0
i.e. at xA = (3600/22) = 163.6
xB= 0.4xA = 65.4

32. with the value of the objective function being rupees 817.8
Hence we have made an additional profit of rupees (817.8-408.9) = rupees
408.9 and this is the maximum amount we would be prepared to pay for the hire
of the machine for doubling the assembly time.
This is because if we pay more than this amount then we will reduce our
maximum profit below the rupees 408.9 we would have made without the
new machine.
Linear programming example 3
Solve
minimise
4a + 5b + 6c
subject to
a + b >= 11
a - b <= 5
c - a - b = 0
7a >= 35 - 12b
a >= 0 b >= 0 c >= 0
Solution
To solve this LP we use the equation c-a-b=0 to put c=a+b (>= 0 as a >= 0 and
b >= 0) and so the LP is reduced to
minimise
4a + 5b + 6(a + b) = 10a + 11b
subject to
a + b >= 11

33. a - b <= 5
7a + 12b >= 35
a >= 0 b >= 0
From the diagram below the minimum occurs at the intersection of a - b = 5 and
a + b = 11
i.e. a = 8 and b = 3 with c (= a + b) = 11 and the value of the objective function
10a + 11b = 80 + 33 = 113.
Linear programming example 4
Solve the following linear program:
maximise 5x1 + 6x2
subject to

34. x1 + x2 <= 10
x1 - x2 >= 3
5x1 + 4x2 <= 35
x1 >= 0
x2 >= 0
Solution
It is plain from the diagram below that the maximum occurs at the intersection
of
5x1 + 4x2 = 35 and
x1 - x2 = 3
Solving simultaneously, rather than by reading values off the graph, we have
that
5(3 + x2) + 4x2 = 35
i.e. 15 + 9x2 = 35
i.e. x2 = (20/9) = 2.222 and
x1 = 3 + x2 = (47/9) = 5.222
The maximum value is 5(47/9) + 6(20/9) = (355/9) = 39.444

35. Linear programming example 5
A carpenter makes tables and chairs. Each table can be sold for a profit of
rupees 30 and each chair for a profit of rupees 10. The carpenter can afford to
spend up to 40 hours per week working and takes six hours to make a table and
three hours to make a chair. Customer demand requires that he makes at least
three times as many chairs as tables. Tables take up four times as much storage
space as chairs and there is room for at most four tables each week.
Formulate this problem as a linear programming problem and solve it
graphically.
Solution
Variables
Let
xT = number of tables made per week
xC = number of chairs made per week

36. Constraints
 total work time
6xT + 3xC <= 40
 customer demand
xC >= 3xT
 storage space
(xC/4) + xT <= 4
 all variables >= 0
Objective
maximise 30xT + 10xC
The graphical representation of the problem is given below and from that we
have that the solution lies at the intersection of
(xC/4) + xT = 4 and 6xT + 3xC = 40
Solving these two equations simultaneously we get xC = 10.667, xT = 1.333 and
the corresponding profit = rupees 146.667

37. Additional problems for exercise: Chapter 2 of Operation
Research book by H A Taha