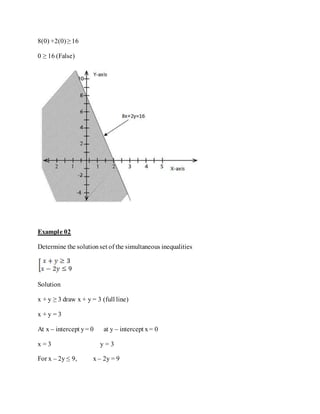
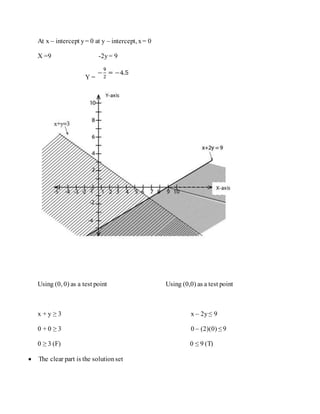
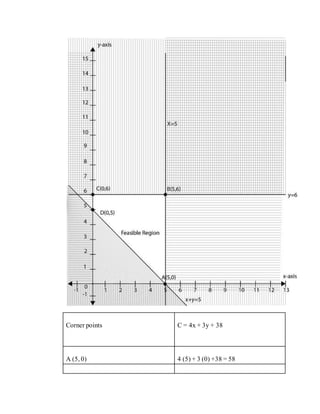
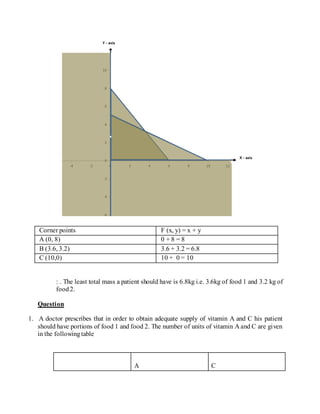
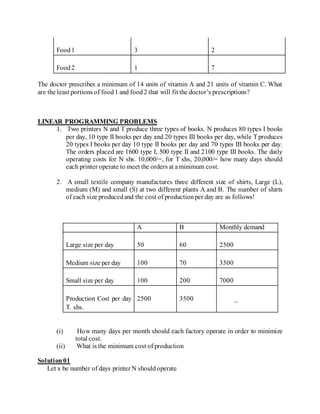
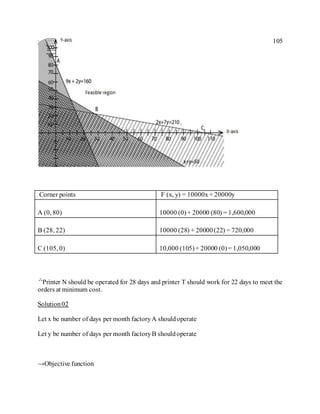
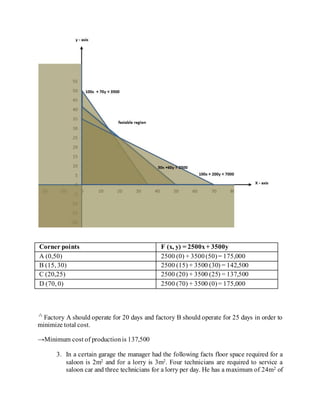
The document defines linear programming as a branch of mathematics used to find the optimal solution to problems with constraints. It provides examples of using linear programming to maximize profit or minimize costs in organizations. It also introduces drawing linear inequalities and solving simultaneous inequalities. The steps to formulate a linear programming problem are identified as defining variables and objectives, translating constraints, finding feasible solutions, and evaluating objectives to find optimal solutions.

1. LINEAR PROGRAMING
Definition
Is a branch of mathematics which enables one to solve problems which either the greatest or
minimum/least value of a certain quantity is required under some given limitations or
constraints.
Example
In a big – organization, decision about distribution in order to realize maximum profit or
reduce costs of productionare done by use of linear programming.
Limitation/ constraints are translatedbylinear inequalities.
Greatest value or least value will be expressedas a function (calledthe objective function)
Introduction
Drawing of linear inequalities
Example 01
Draw and show the half plane representedby 8x+2y ≥16
Solution
For 8x +2y≥16; draw 8x+ 2y = 16
For x – intercept, y = 0
8x = 16
X = 2
For y – intercept, x = 0
2y = 16
Y = 8
Using (0, 0) as a test point

2. 8(0) +2(0)≥ 16
0 ≥ 16 (False)
Example 02
Determine the solutionset of the simultaneous inequalities
Solution
x + y ≥ 3 draw x + y = 3 (full line)
x + y = 3
At x – intercept y= 0 at y – intercept x= 0
x = 3 y = 3
For x – 2y ≤ 9, x – 2y = 9

3. At x – intercept y= 0 at y – intercept, x= 0
X =9 -2y= 9
Y =
Using (0, 0) as a test point Using (0,0) as a test point
x + y ≥ 3 x – 2y≤ 9
0 + 0 ≥ 3 0 – (2)(0) ≤ 9
0 ≥ 3 (F) 0 ≤ 9 (T)
 The clear part is the solutionset

4.  The solutionset is calledthe feasible region
Questions
Draw by shading unwanted regions of the half planes represented by following
simultaneous inequalities
(i) y≥ 2x – 1, y ≤ -1
(ii) y≤ 2x – 1, y ≥ x – 3, y ≥ -1
(iii) y < 2x – 1, y ≤ -1
(iv) 6x + 9y ≥ 12
0.4x+ 0.1y≥ 0.2
32x+ 10y≥ 20
Evaluationofa functionsatisfiedbythe givenset ofinequalities
→Example
Find the maximum and minimum value of c = 4x + 3y + 38 subjectedto
x + y ≥ 5
0 ≤ y ≤ 6 0 ≤ x ≤ 5
x ≥ 0, y ≥ 0
Solution
For x + y ≥ 5
x + y = 5
When x = 0, y = 5
y = 0, x = 5
For 0 ≤ y ≤ 6
0 = y = 6
Line y = 6
For 0 ≤ x ≤ 5
O = x = 5
Line x = 5
Test points x ≥ 0, shade left of x = 0
(0, 0) y ≥ 0, shade below of x = axis

5. Corner points C = 4x + 3y + 38
A (5, 0) 4 (5) + 3 (0) +38 = 58

6. B (5, 6) 4 (5) + 3 (6) + 38 = 76
C (0, 6) 4 (0) + 3 (6) +38 = 56
D (0, 5) 4 (0) + 3 (5) + 38 = 53
: . The maximum value of c = 76 and occurs at (5, 6)
The minimum value of c = 53 and occurs at (0, 5)
Questions
1. Find the maximum and minimum values of the given functions and the value
x and y where they occur
(i) Z = 4x+ 3y
Subject to
x + 2y ≤ 10
3x + y ≤ 5
x ≥ 0, y ≥ 0
(ii) P = 134x+ 20y
Subject to
x + y ≤ 160
10 ≤ x ≤ 60
0 ≤ y ≤ 120
(iii) T = 4x +7y
Subject to.
x + y ≤ 18
5 ≤ x ≤ 10
3 ≤ y ≤ 10
x ≥ 0, y ≥ 0
(iv) P = 2x + 4y
Subject to
2x + 3y ≥ 3
-5x+ 4y ≤ 0
3x + 4y ≤ 18
X ≥ 0, y ≥ 0.
FORMULATION OF A LINEAR PROGRAMMING PROBLEM.
Steps in formulatinga linear programming problem.
1. * Read the problem several times and assess what is known and what is to be determined.

7. 2. * Identify the unknown quantities and assign variables to them, be careful about the units.
3. * Determine the objective function;it involves the quantity to be maximized or minimized.
4. * Translate the constraints into linear inequalities,
* Constraints are limitation or restrictions to the problem for each constraints the units must
be same.
5. * Graph the constraints andfind the feasible solution
6. * Find the corner points of the feasible solution. These are points of intersectionof the graph
7. * Evaluate the objective function. Highest value of the objective function has to be
maximized or smallest value to be minimized.
Example
A student has 120 shillings to spend on exercise books. At a school shop an exercise
book costs 8 shillings, at stationery store an exercise book costs 12 shillings. The school
has only 6 exercise books and the student wants to obtain the greatest number of exercise
books possible usingthe money. Find the greatest number of exercise books he canbuy.
Solution
Let x be number of exercise books to be bought at school shop
Let y be number of exercise books to be bought at stationeryshop
→Objective function
Let f (x, y) = objective function
Then f (x, y) = x + y
→Constrains or linear inequalities
8x + 12y ≤ 120
x ≤ 6
Non – Negative constraints
x ≥ 0
y ≥ 0
→Equations
8x + 12y = 120
4x + 6y = 60
2x + 3y = 30
When x = 0, y = 10
y = 0, x = 15
x = 6, y = 0

8. x = 6
Corner points F (x, y) = x + y
A (0, 0) 0 + 0 = 0
B (6, 0) 6 + 0 = 6
C ( 6, 6) 6 + 6 = 12
D (0, 10) 0+10 = 10

9. : . The greatest numbers of exercise books he can buy are 12 books 6 from the school
shop and 6 from stationery.
Example
Student in a certain class are about to take a certain test of BAM which has two sections
A and B; where in section A each question worth 10 marks while in section B; each
worth 25 marks. The student must do at least 3 questions of section A; but not more than
12. A student must also do 4 questions from section B but not more than 15. In addition
students cannot do more than 20 questions. How many questions of each type should the
student do to obtain the maximum scores?
Solution
Let x be number of questions to be done in sectionA
Let y be number of questions to be done in sectionB
→Objective function
f (x, y) = 10x+ 25y
→Constrains
3 ≤ x ≤ 12
4 ≤ y ≤ 15
x + y ≤ 20
x ≥ 0, y ≥ 0
Maximize f (x, y) = 10x+ 25ysubject to;
3 ≤ x ≤ 12
4 ≤ y ≤ 15
x + y ≤ 20
x ≥ 0, y ≥ 0
Equations
3 = x = 12
4 = y = 15
x + y = 20
x = 20, y = 0
x = 0, y = 20
x = 0

10. y = 0
Corner Points f(x, y) = 10x+ 25y
A (3, 4) 10 (3) + 25 (4) = 130
B (12, 4) 10 (12) + 25 (4) = 220
C (12, 8 ) 10 (12) + 25 (8) = 320
D (5, 15) 10 (5) + 25 (15) = 425
E (3, 15) 10 (3) + 25 (15) = 405
The student should do 5 questions from section A and 15 questions from section B to
obtain maximum score of 425.
Diet problems onlinear programming problem
Example 01
A doctor prescribes a special diet for patients containing the following number of units of
Vitamin A and B per kg of two types of foodF1 and F2
Type of Food Vitamin A Vitamin B
F1 20 units/kg 7 units/kg
F2 15 units /kg 14 units /kg

11. If the minimum daily intake required is 120 units of A and 70 units of B, what is the least
total mass of fooda patient must have so as to have enough of these vitamins?
EXAMPLE 02
Rice and beans provide maximum levels of protein, calories and vitamin B2. If used as a
staple diet. The food values per kg of uncooked rice and beans are as shown in the table
below.
Protein/kg Calories/kg Vitamin B2/kg Price kg
Rice 60g 3200 cal 0.4 400
Beans 90g 1000 cal 0.1 500
Min daily req. 120 2000 cal 0.2
What is the lowest cost of diet meeting, these specifications?
Solution.
Let x be number of kg of rice to be bought
Let y be number of kg of beans to be bought
→Objective function
400x+ 500y
Constrains
60x+ 90y≤ 120
3200x+ 1000y≤ 2000
0.4x + 0.1y≤ 0.2
Minimize f (x, y) = 400x+ 500ySubject to;
60x+ 90y≤ 120
3200x+ 1000y≤ 2000

12. 0.4x+ 0.1y≤ 0.2
x ≥ 0, y ≥ 0
For 60x+ 90y≥ 120
60x+ 90y= 120
2x + 3y = 4
When x = 0, y = 1.3
Y = 0, x = 2
For 3200x+ 1000y≥ 2000
32x+ 10y= 20
16x+ 5y = 10
When x = 0, y = 2
Y = 0, x = 0.63
For 0.4x + 0.1y ≤ 0.2
0.4x+ 0.1y= 0.2
When x = 0, y = 2
When y = 0, x = 0.5

13. Corner points F (x, y) = x + y
A (0, 8) 0 + 8 = 8
B (3.6, 3.2) 3.6 + 3.2 = 6.8
C (10,0) 10 + 0 = 10
: . The least total mass a patient should have is 6.8kg i.e. 3.6kg of food 1 and 3.2 kg of
food2.
Question
1. A doctor prescribes that in order to obtain adequate supply of vitamin A and C his patient
should have portions of food 1 and food 2. The number of units of vitamin A and C are given
in the followingtable
A C

14. Food1 3 2
Food2 1 7
The doctor prescribes a minimum of 14 units of vitamin A and 21 units of vitamin C. What
are the least portions of food1 and food2 that will fit the doctor’s prescriptions?
LINEAR PROGRAMMING PROBLEMS
1. Two printers N and T produce three types of books. N produces 80 types I books
per day, 10 type II books per day and 20 types III books per day, while T produces
20 types I books per day 10 type II books per day and 70 types III books per day.
The orders placed are 1600 type I, 500 type II and 2100 type III books. The daily
operating costs for N shs. 10,000/=, for T shs, 20,000/= how many days should
each printer operate to meet the orders at aminimum cost.
2. A small textile company manufactures three different size of shirts, Large (L),
medium (M) and small (S) at two different plants A and B. The number of shirts
of each size producedand the cost of productionper day are as follows!
A B Monthly demand
Large size per day 50 60 2500
Medium size per day 100 70 3500
Small size per day 100 200 7000
Production Cost per day
T. shs.
2500 3500 _
(i) How many days per month should each factory operate in order to minimize
total cost.
(ii) What is the minimum cost of production
Solution01
Let x be number of days printer N shouldoperate

15. Let Y be number of days printer T should operate
→Objective function(f(x, y))
10000x+ 20000y
→Constrains
 80x + 20y≥ 1600
 10x + 10y≥ 500
 20x + 70y≥ 2100
 X ≥ 0, y ≥ 0
→Equations
 80x + 20y≥ 1600
80x+ 20y= 1600
8x + 2y = 160
When x = 0, y = 80
y = 0, x = 20
 10x + 10y≥ 500
10x+ 10y= 500
x + y = 50
When x = 0, y = 50
y = 0, x = 50
 20x + 70y≥ 2100
20x+ 70y= 2100
2x + 7y = 210
When x = 0, y = 30

16. y = 0, x = 105
Corner points F (x, y) = 10000x+ 20000y
A (0, 80) 10000 (0)+ 20000 (80) = 1,600,000
B (28, 22) 10000 (28) + 20000(22) = 720,000
C (105, 0) 10,000 (105)+ 20000 (0)= 1,050,000
Printer N should be operated for 28 days and printer T should work for 22 days to meet the
orders at minimum cost.
Solution02
Let x be number of days per month factoryA shouldoperate
Let y be number of days per month factoryB shouldoperate
→Objective function

17. F (x, y) = 2500x+ 3500y
→Constrains
 50x + 60y≥ 2500
 100x+ 70y ≥ 3500
 100x+ 200y≥ 7000
 x ≥ 0, y ≥ 0
Minimize f (x, y) = 2500x+ 3500y
Subject to 50x+ 60y≥ 2500
100x+ 70y≥ 3500
100x+ 200y≥ 7000
X ≥ 0, y ≥ 0
→Equations
 50x + 60y= 2500
When y = 0, x = 50
X = 0, y = 41.7
 100x+ 70y = 3500
When y = 0, x = 35
x = 0, y = 50
 100x+ 200y= 7000
When y = 0, x = 70
X = 0, y = 35

18. Corner points F (x, y) = 2500x+ 3500y
A (0,50) 2500 (0) + 3500(50)= 175,000
B (15, 30) 2500 (15) + 3500 (30) = 142,500
C (20,25) 2500 (20) + 3500 (25) = 137,500
D (70, 0) 2500 (70) + 3500 (0)= 175,000
Factory A should operate for 20 days and factory B should operate for 25 days in order to
minimize total cost.
→Minimum cost of productionis 137,500
3. In a certain garage the manager had the following facts floor space required for a
saloon is 2m2 and for a lorry is 3m2. Four technicians are required to service a
saloon car and three technicians for a lorry per day. He has a maximum of 24m2 of

19. a floor space and a maximum of 36 technicians available; in addition he is not
allowed to service more Lorries than saloon cars. The profit for serving a saloon
car is 40,000/= and a lorry is 60,000/=. How many motor vehicles of each type
should be serviceddaily in order to maximize the profit?
Solution
Let x be number of salooncars to be serviceddaily
Let y be number of Lorries to be serviceddaily
→Objective function
F (x, y) = 40000x+ 60000y
→Constrains
 2x + 3y ≤ 24
 4x + 3y ≤ 36
 x ≥ y
 x ≥ 0 and y ≥ 0
Maximize f (x, y) = 40000x+ 60000y
Subject to 2x + 3y ≤ 24
4x + 3y ≤ 36
x ≥ y
x ≥ 0 and y ≥ 0
→Equations
 2x + 3y ≤ 24
When x = 0, y = 8

20. Y = 0, x = 12
 4x + 3y ≤ 36
When x = 0, y = 12
y = 0, x = 9
 x = y
Corner points F (x, y) = 40000x+ 60000y
A (0, 0) 40000 (0) + 60000(0) = 0
B (4.8, 4.8) 40000 (4.8) + 60000 (4.8) = 480,000
C (6,4) 40000 (6)+ 60000 (4) = 480,000
D (9, 0) 40000 (9) + 60000 (0) = 360,000
6 salooncars and 4 Lorries shouldbe serviceddaily to maximize profit to 480,000/=

21. More example
A builder has two stores, one at S1 and the other at S2. He is building houses at P1, P2, and P3.
He needs 5 tons of bricks at P1, 6 tons of bricks at P2 and 4 tons of bricks at P3. The stores
contain 9 tons of bricks at S1 and 6 tons of bricks at S2. The transport cost per ton are shown
in the diagram
To From P1 P2 P3
S1 6/= 3/= 4/=
S2 4/= 2/= 6/=
How does the builder send his bricks at a minimum cost?What is the minimum overall cost?
Solution
Let the builder send x tons of bricks from S1 to P1 and y tons of bricks from S1 to P2
Then the transportationof bricks to P1, P2 and P3 will be as follow: -
To
From P1 P2 P3
S1 X Y 9 – (x +
y)
S2 5 – x 6 – y 4 – [9 –
(x + y)]
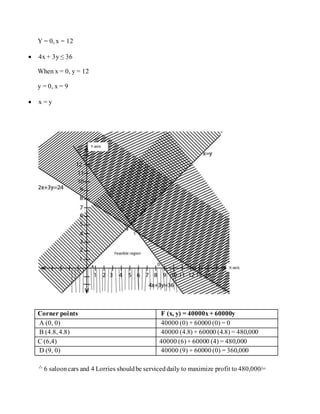
The constrains are obtainedas follows
 x ≥ 0, y ≥ 0
 9 – (x + y) ≥ 0 i.e. x + y ≤ 9
 5 – x ≥ 0 i.e. x ≤ 5
 6 – y ≥ 0 i.e. y ≤ 6
 4 – [9 - (x + y)} ≥ 0 i.e. x + y ≥ 5

22. Objective function
F (x, y) = 6x + 3y + 4(9 - (x + y)) + 4 (5 – x) + 2(6 – y) +6 [4 – (9 - (x + y)]
= 6x + 3y +36 – 4x+ 4y + 20 – 4x+ 12 – 2y + 24 – 54 + 6x+ 6y
F (x, y) = 4x – 3y+ 38
Minimize f (x, y) = 4x – 3y + 38
Subject to x + y ≤ 9
x + y ≥ 5
x ≤ 5, y ≥ 0
y ≤ 6, y ≥ 0
→Equation
 x + y = 9
When x = 0, y = 9
y = 0, x = 9
 x + y = 5
x = 0, y = 5
y = 0, x = 9
 x = 5
 y = 6

23. Corner points F (x, y) = 4x + 3y + 38
A (0, 5) 4 (0) + 3 (5) + 38 = 53
B (0, 6) 4 (0) + 3 (6) + 38 = 56
C (3, 6) 4 (3) + 3 (6) + 38 = 68
D (5, 4) 4 (5) + 3 (4) + 38 = 70
E (5, 0) 4 (5) + 3 (0) + 38 = 58
The builder should send the bricks of tons as follows
To
From P1 P2 P3
S1 0 5 4
S2 5 1 0

24. The overall minimum cost is 53/=
EXERCISE
There is a factory located at each of the places P and Q. From these location a certain
commodity is delivered to each of the three deports situated at A, B and C. The weekly
requirements of the deports are respectively 5,5 and 4 unit of the commodity while the
production capacity of the factories P and Q are 8 and 6 units respectively, just sufficient for
requirement of deports. The cost of transportationper unit is given.
To
From A B C
P 16 10 15
Q 10 12 10
Formulate this linear programming problem and how the commodities can be transported at
minimum cost. What is the overall minimum cost?