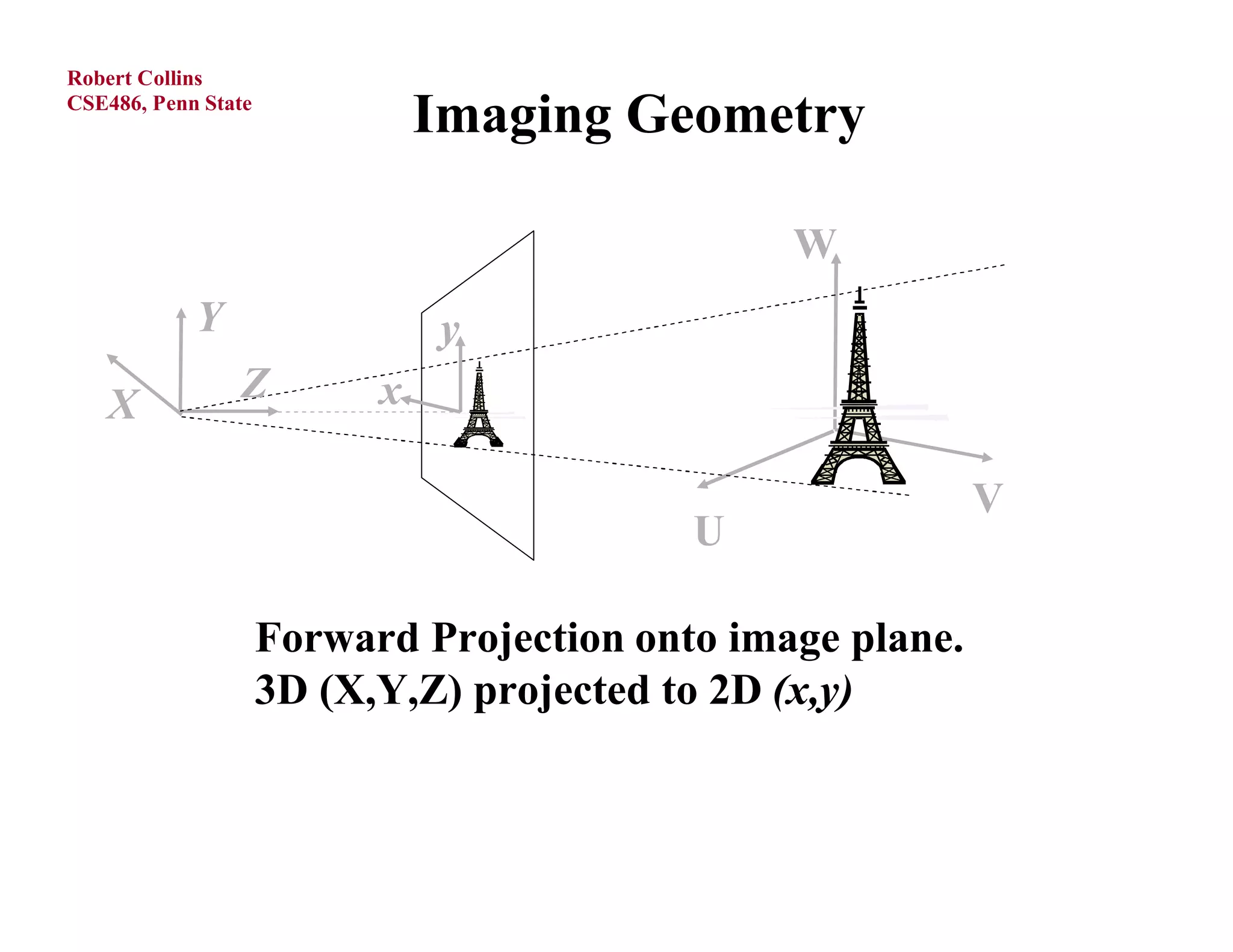
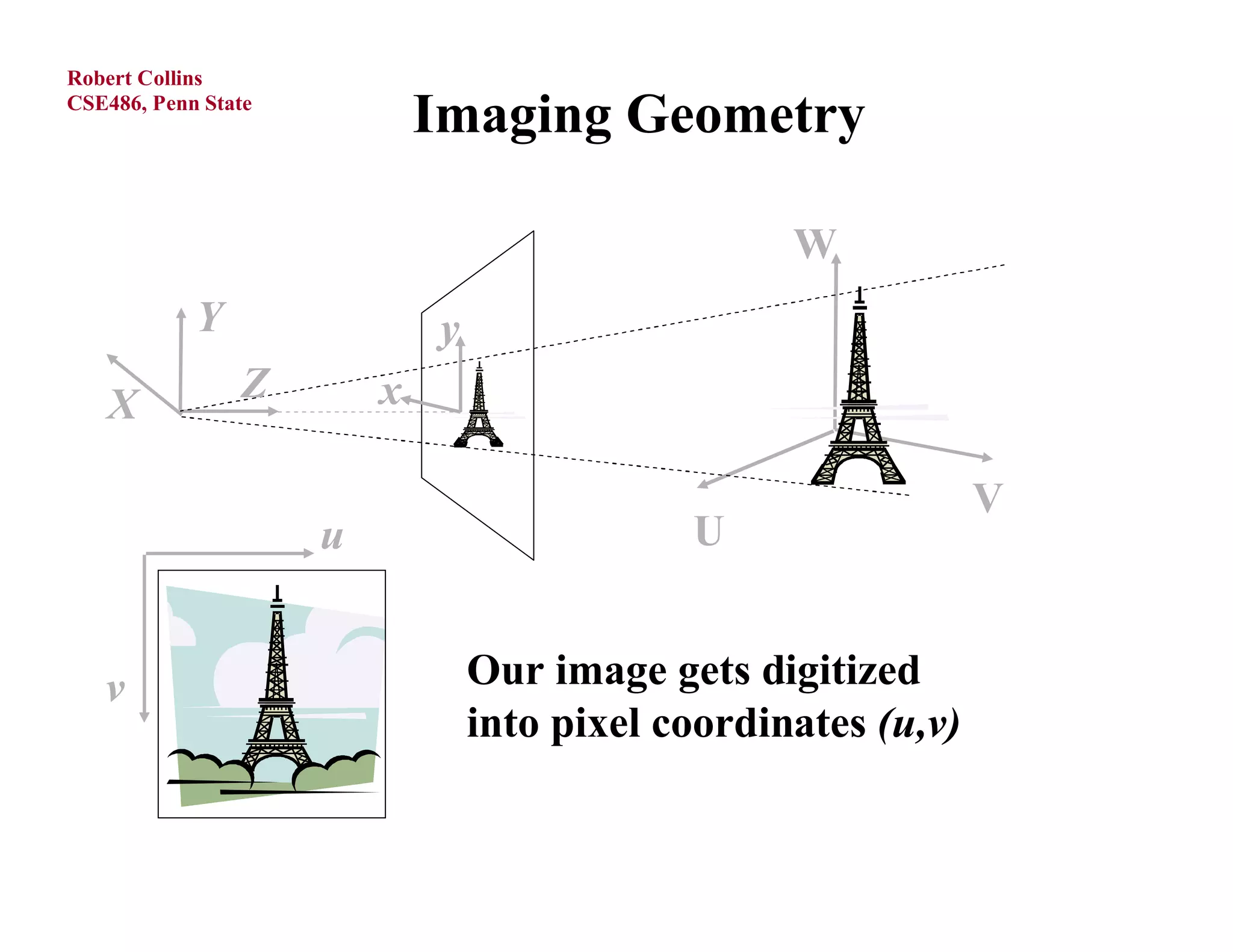
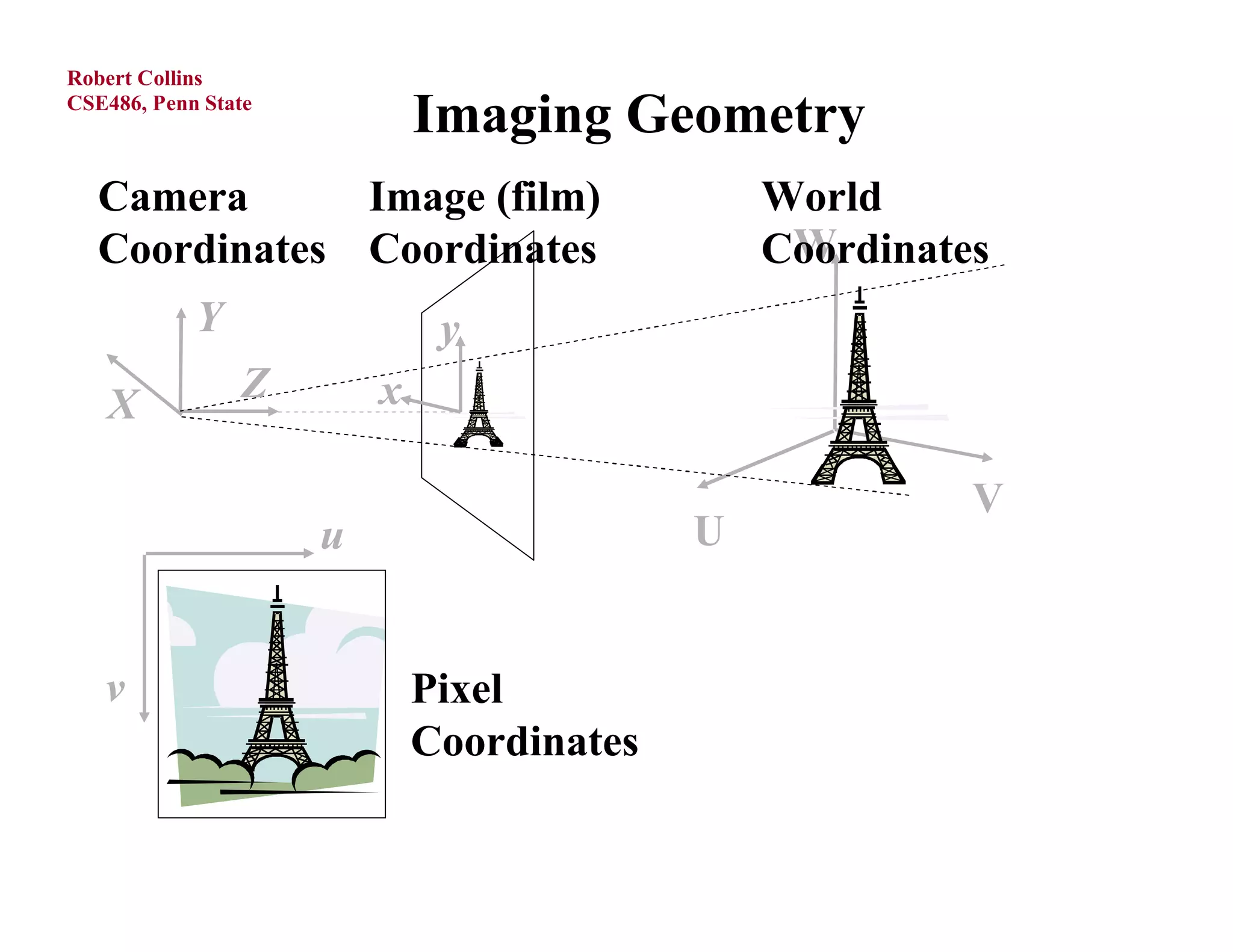
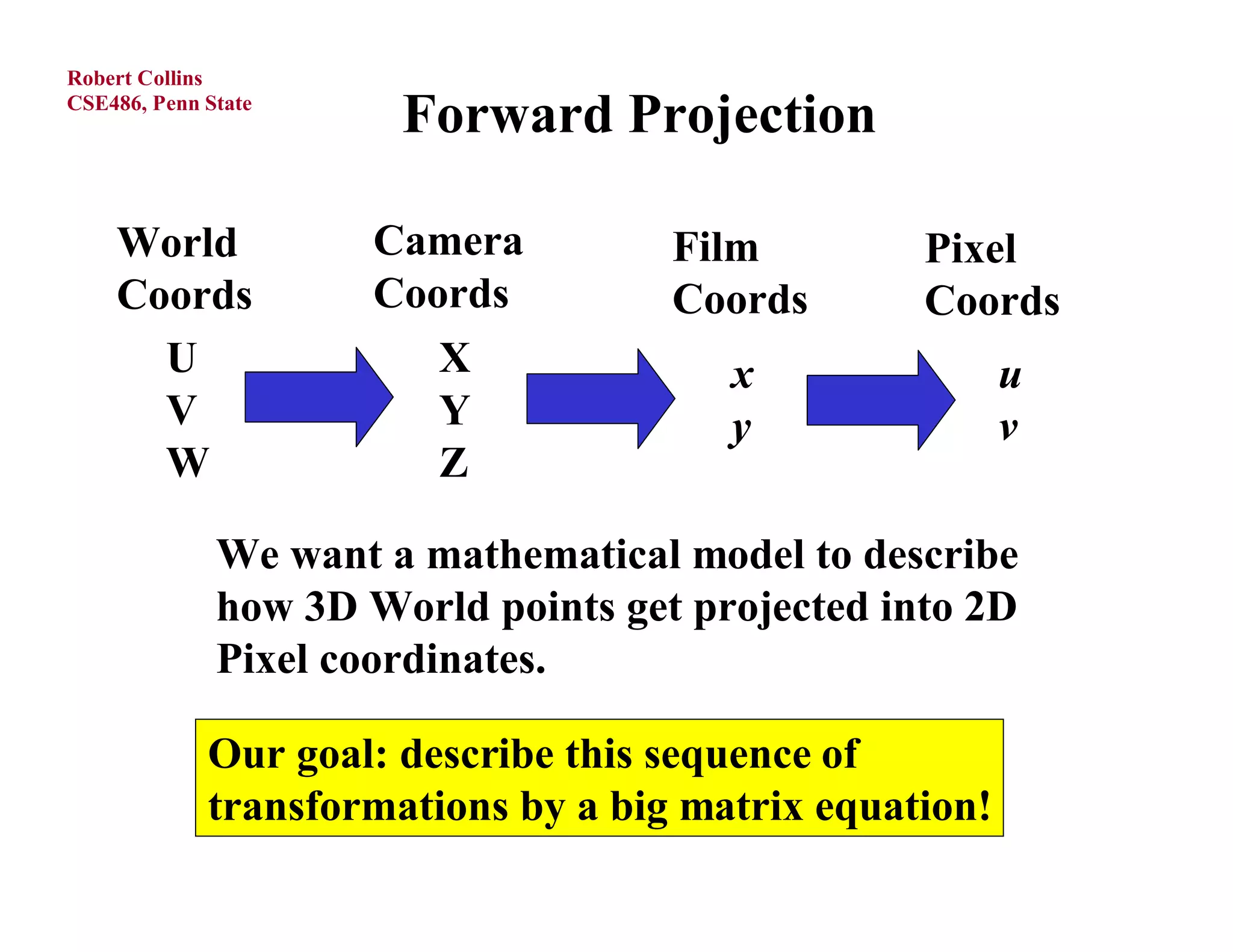
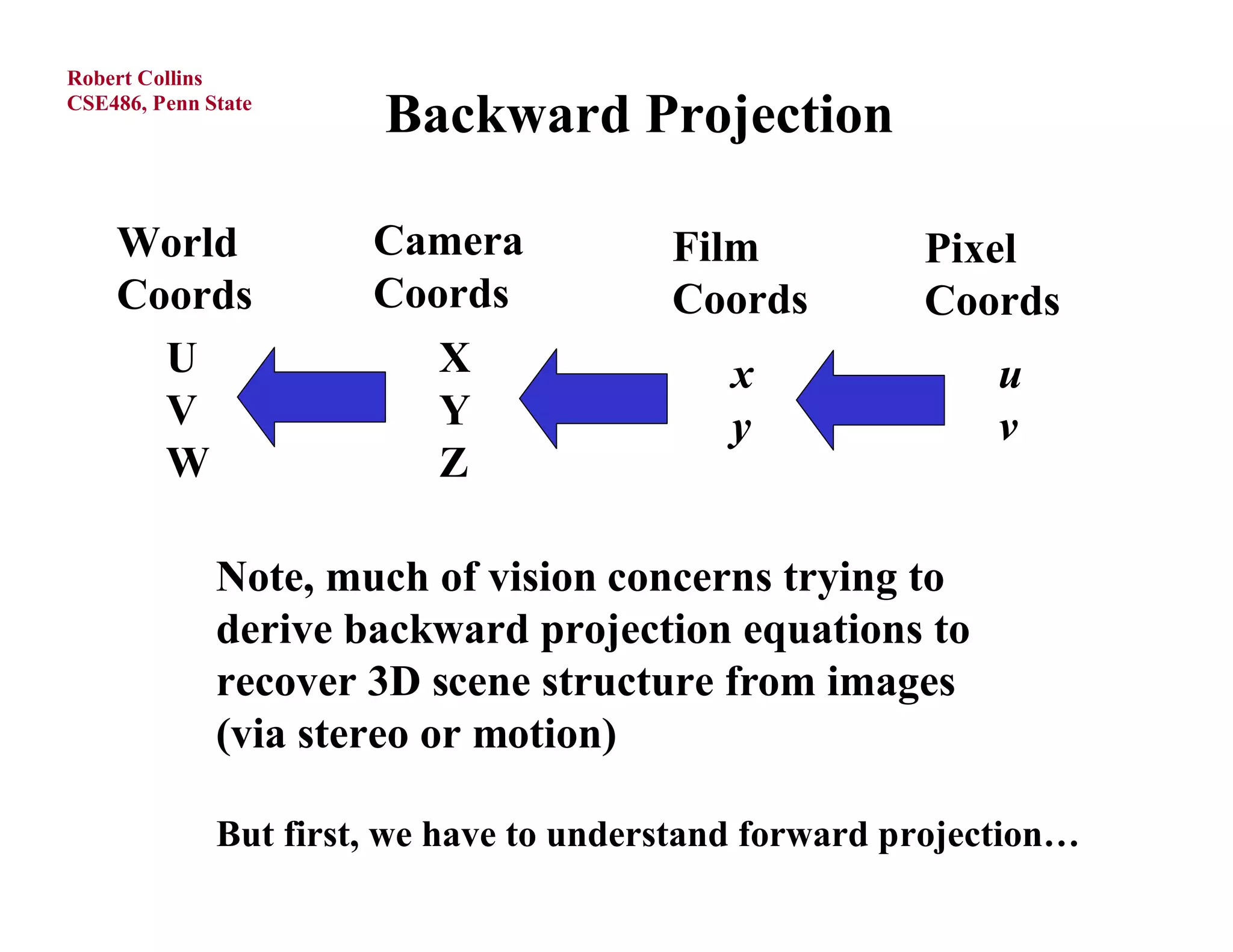
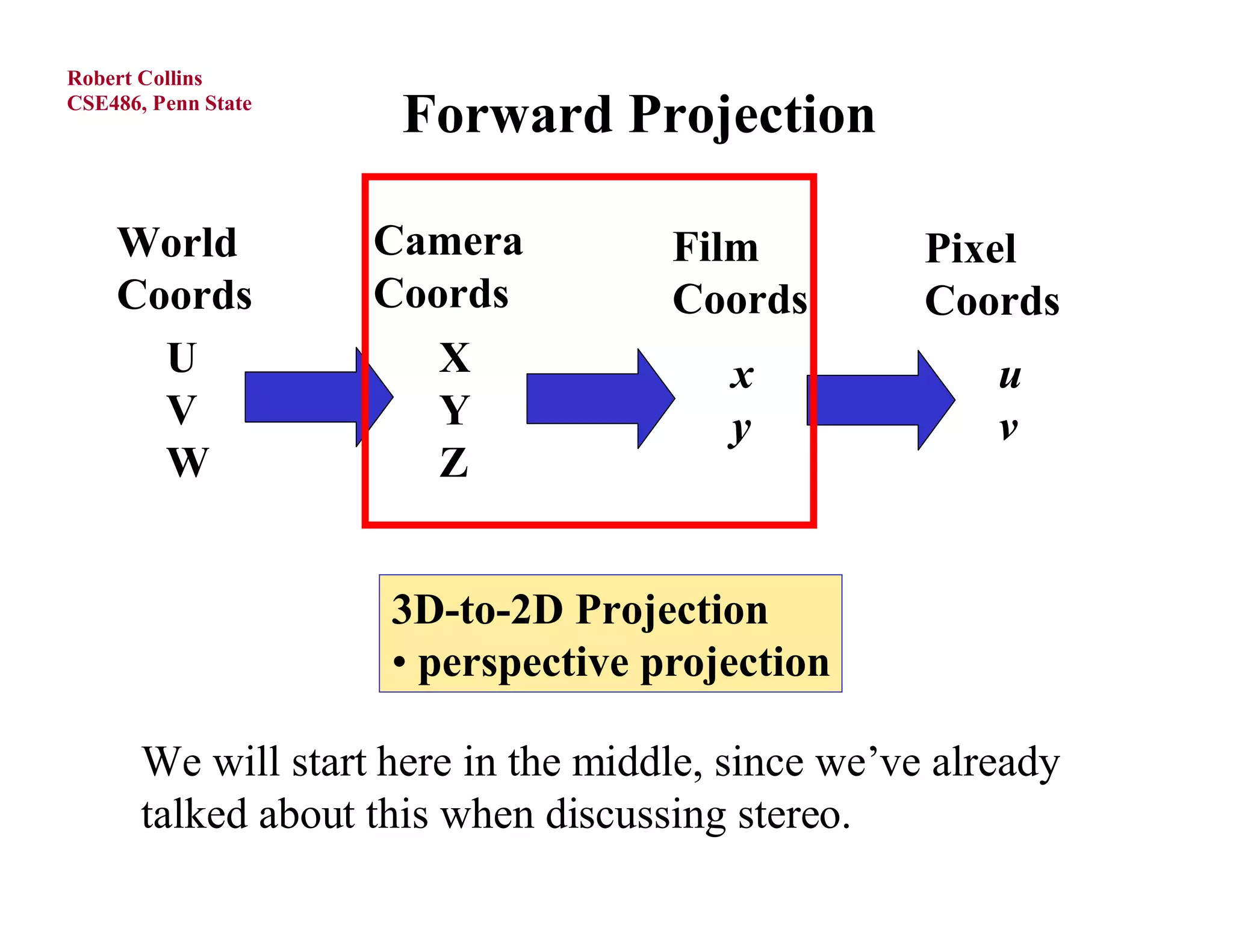
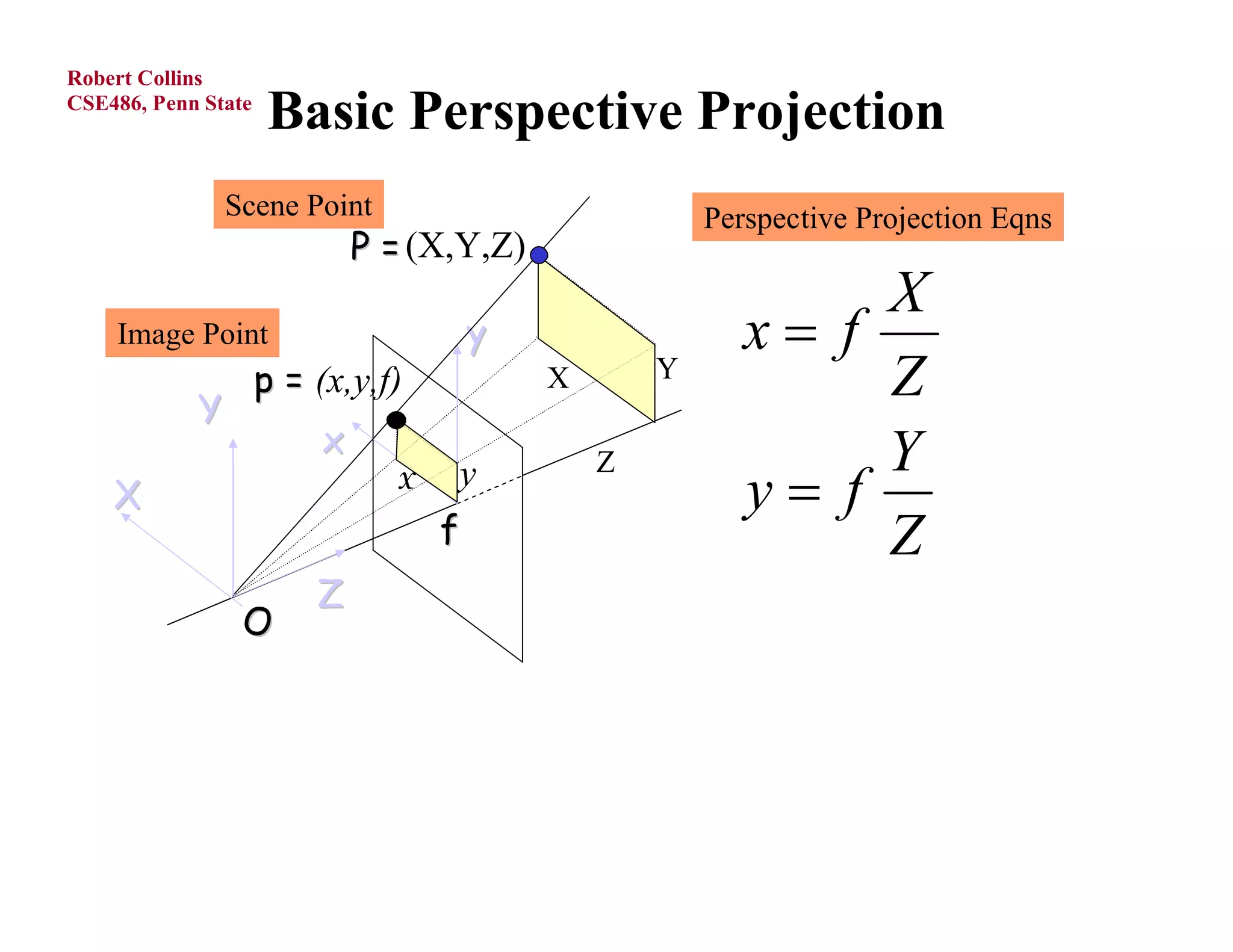
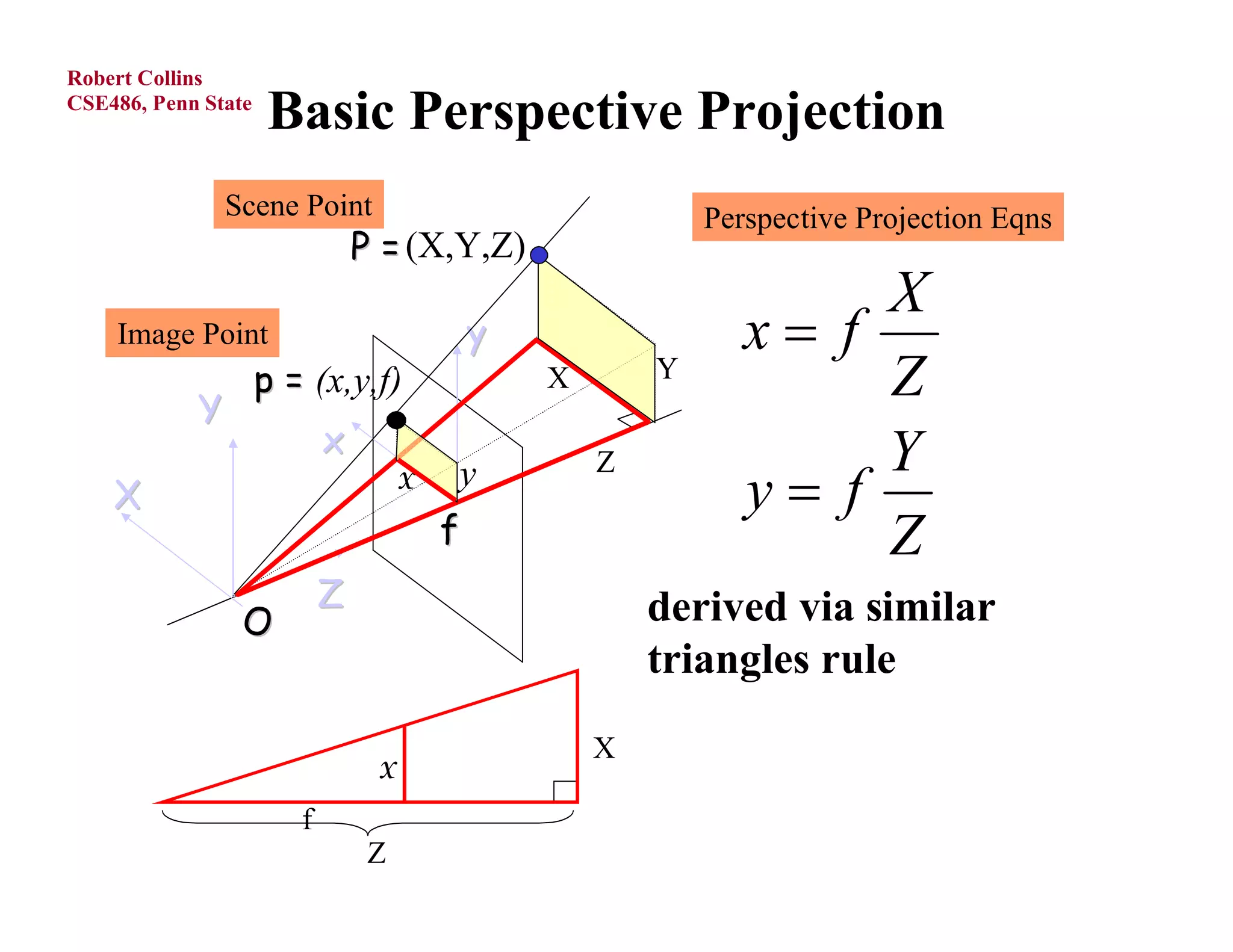
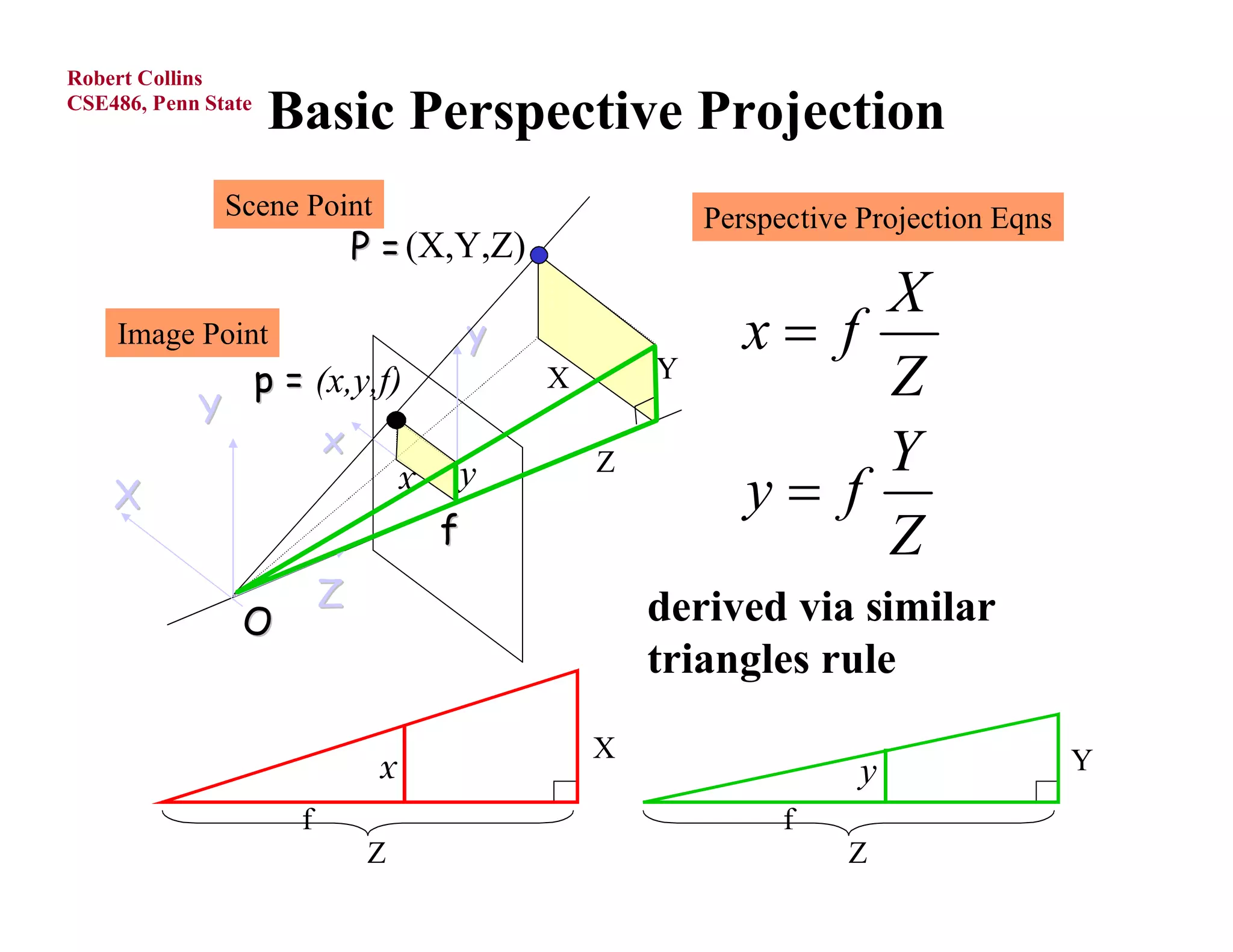
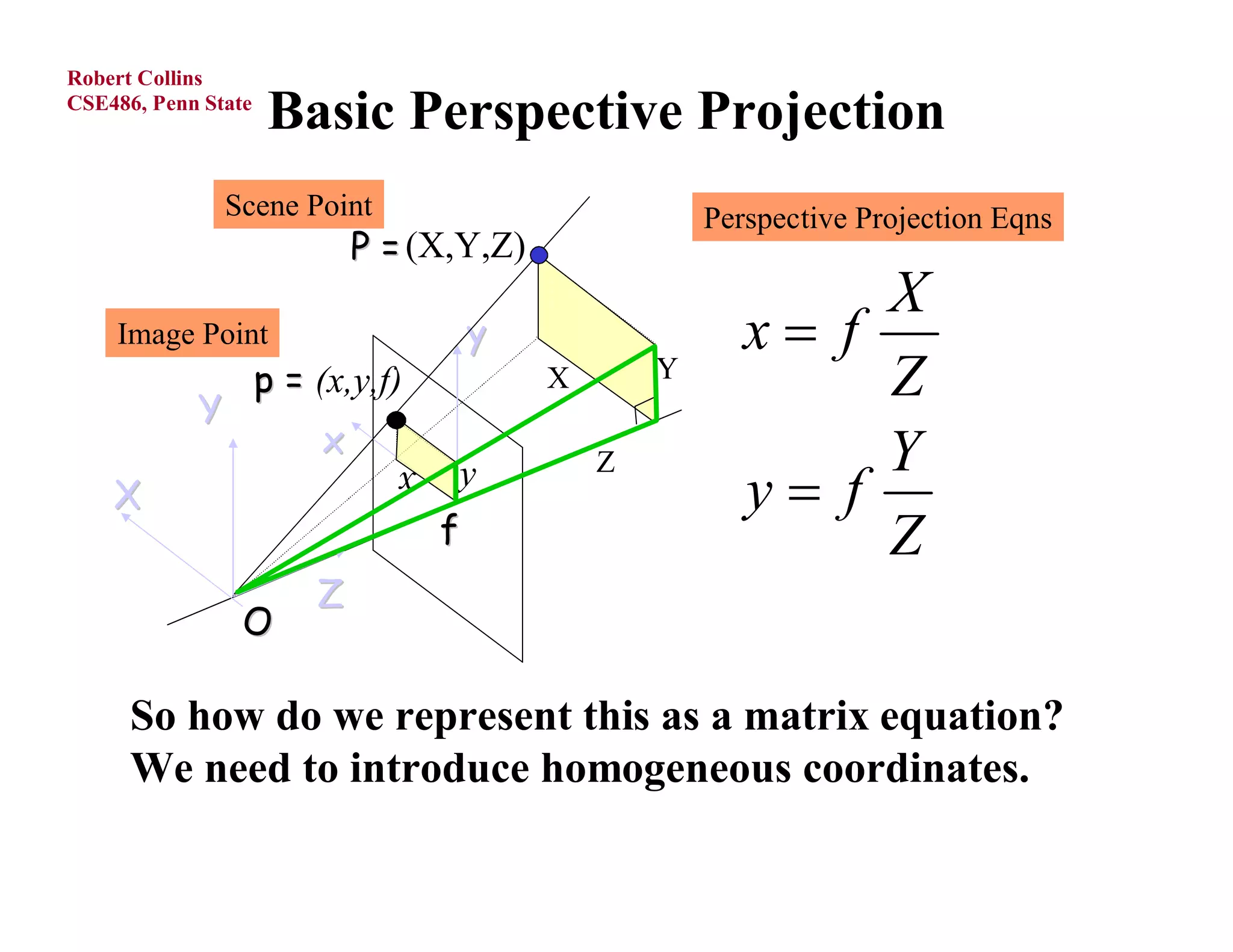
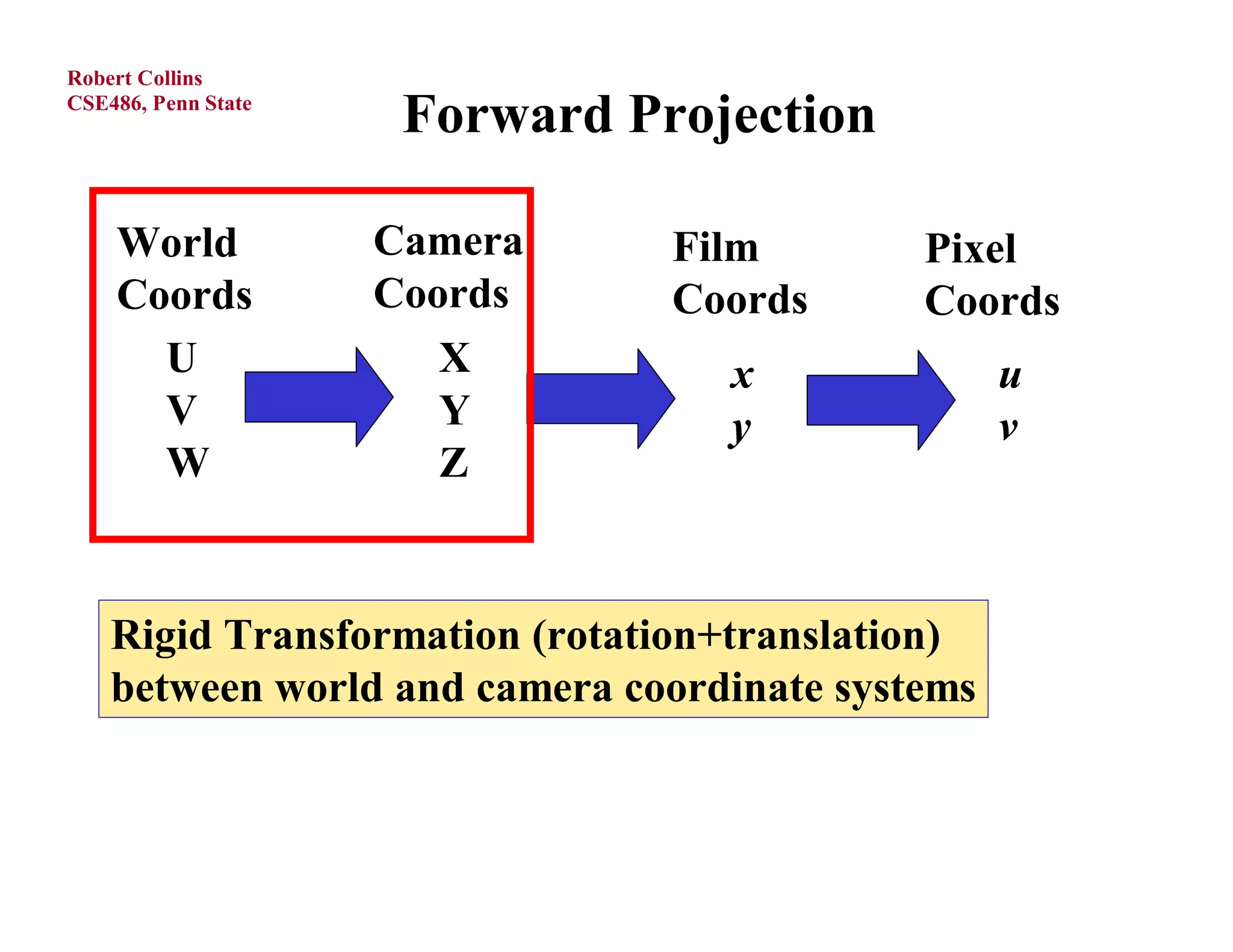
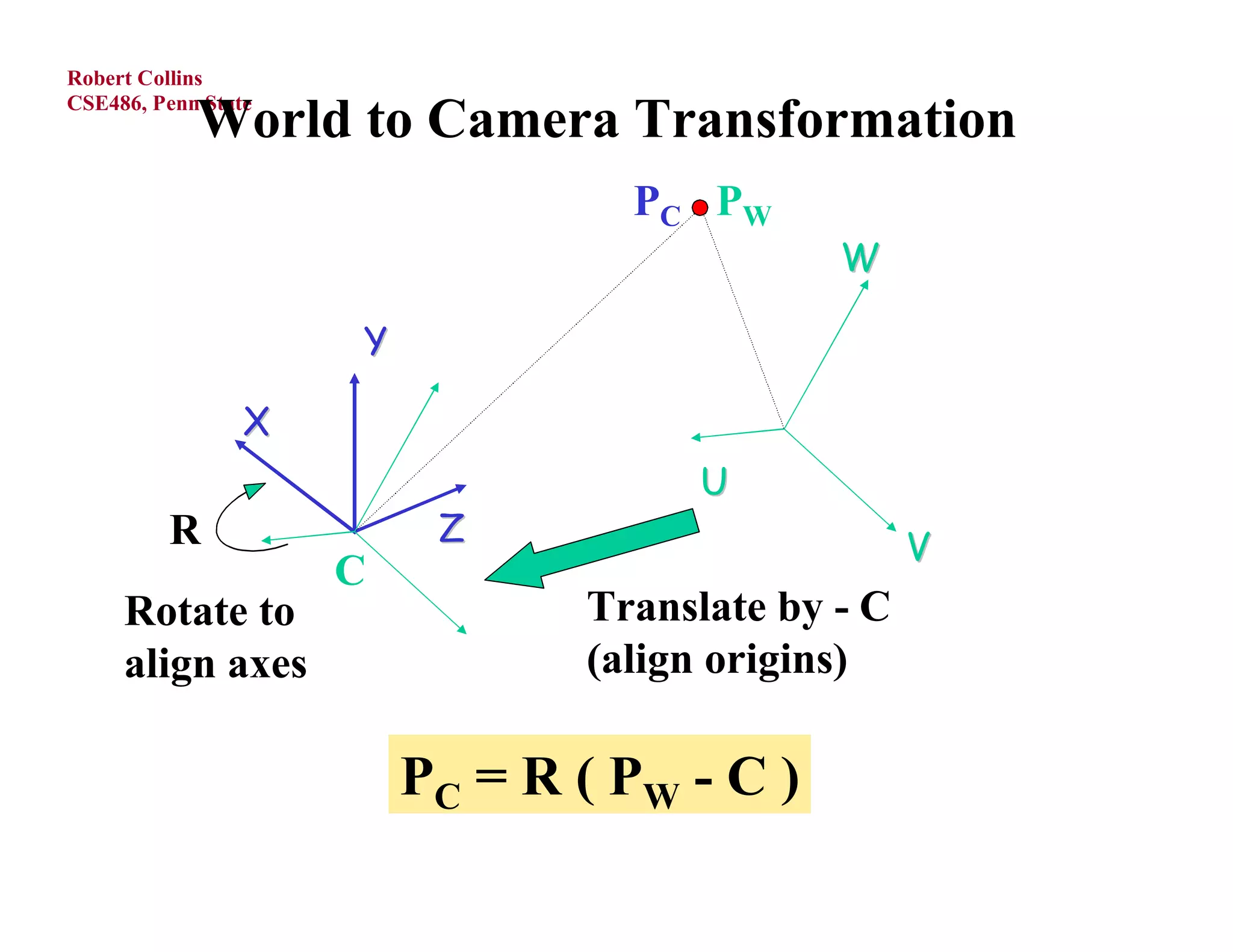
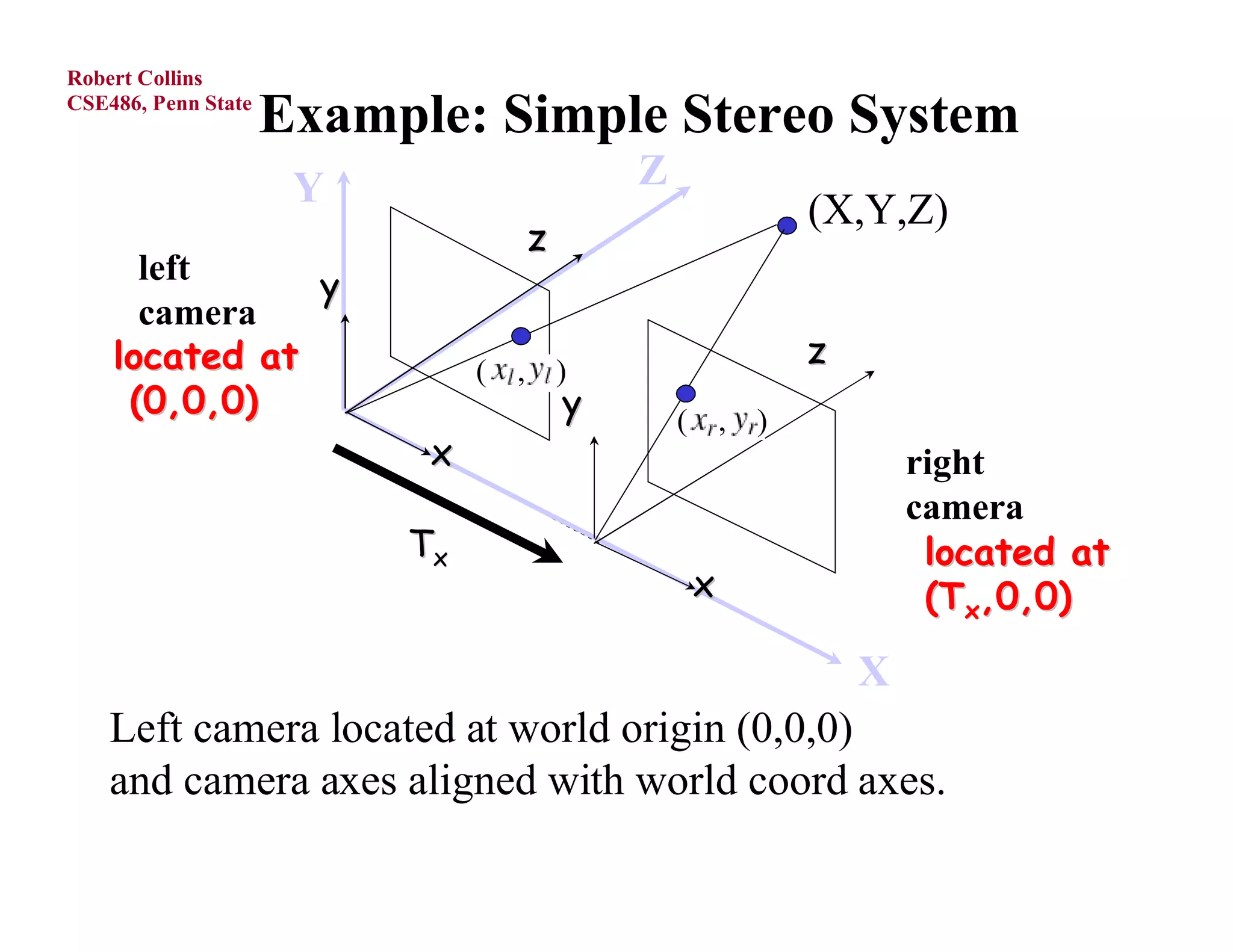
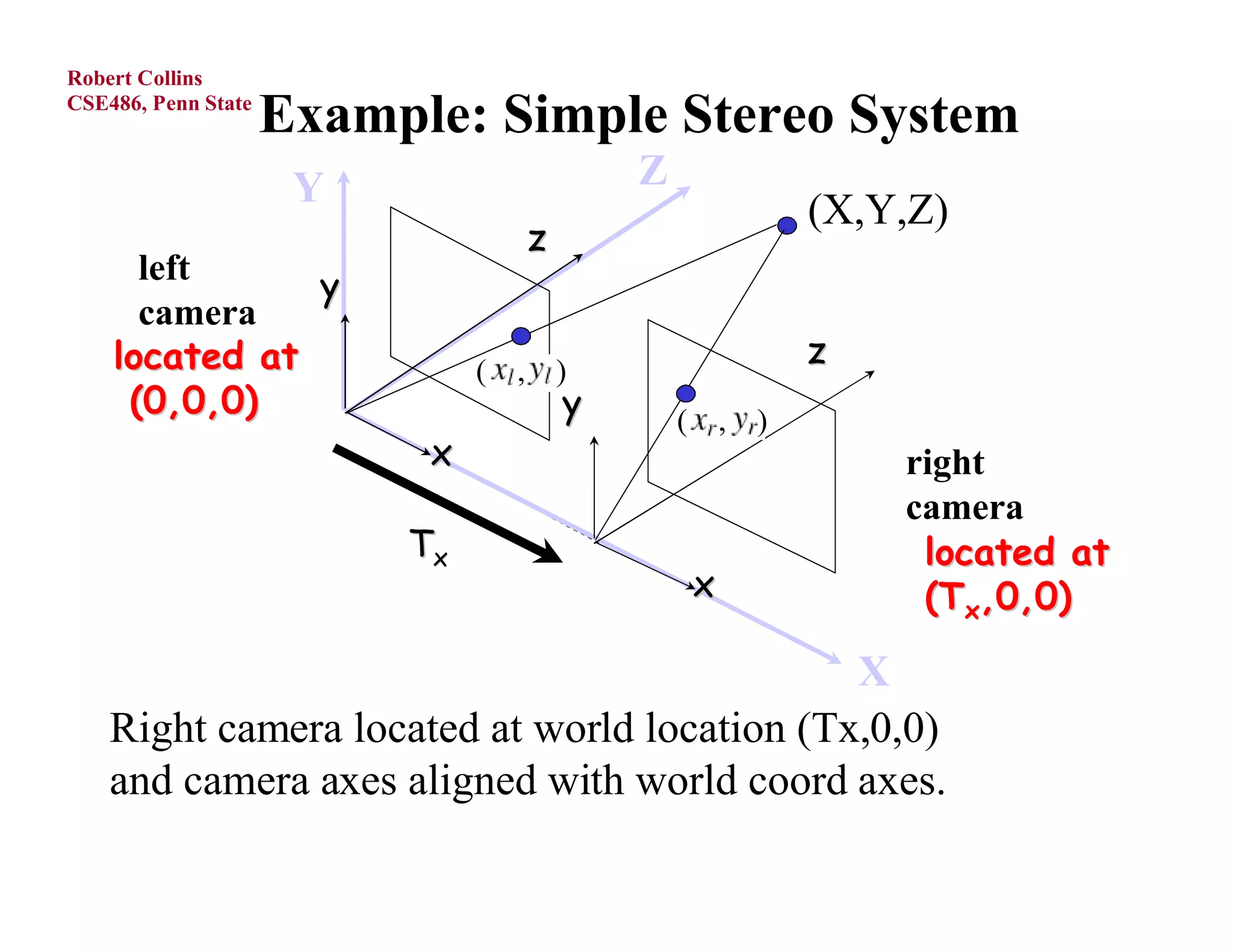
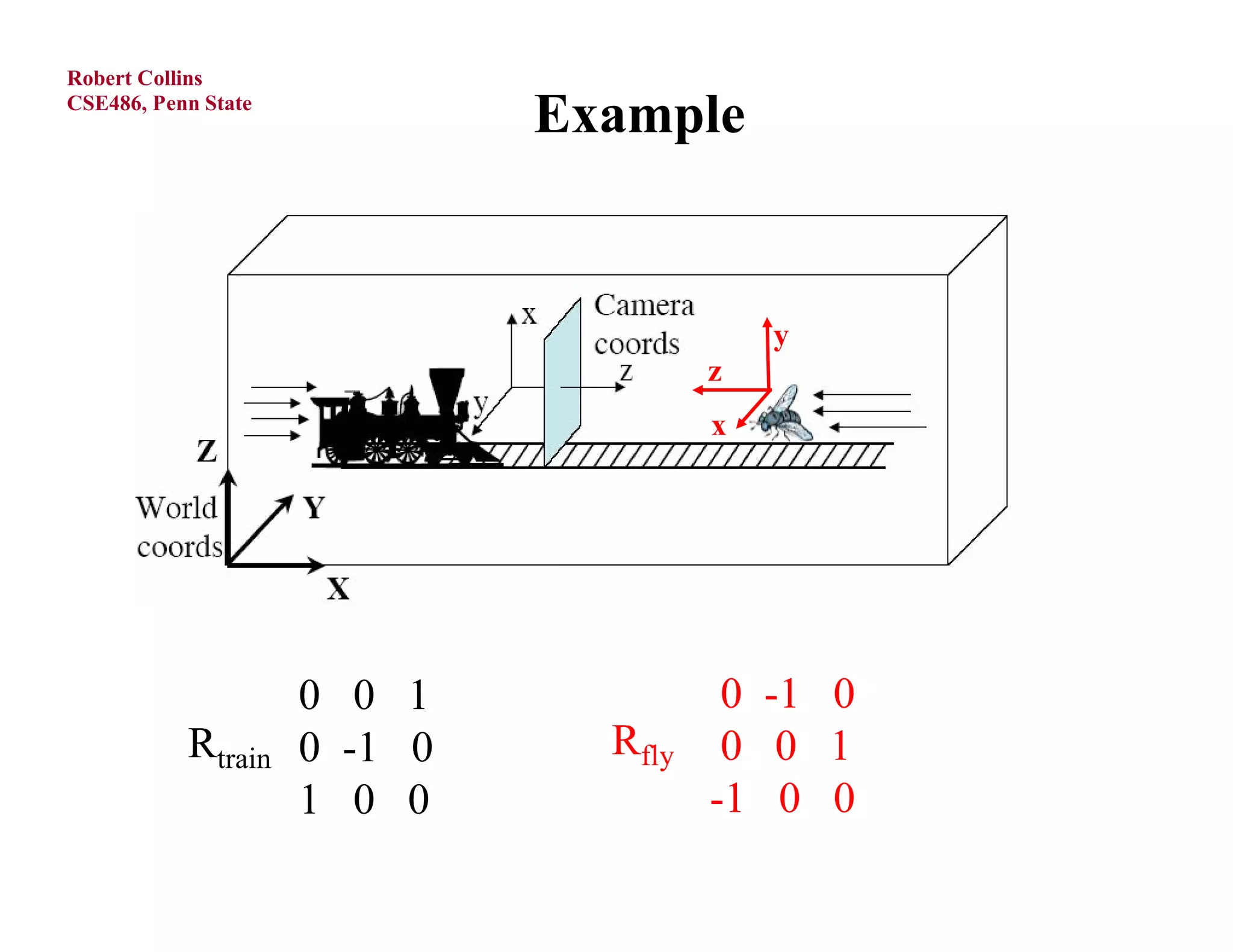
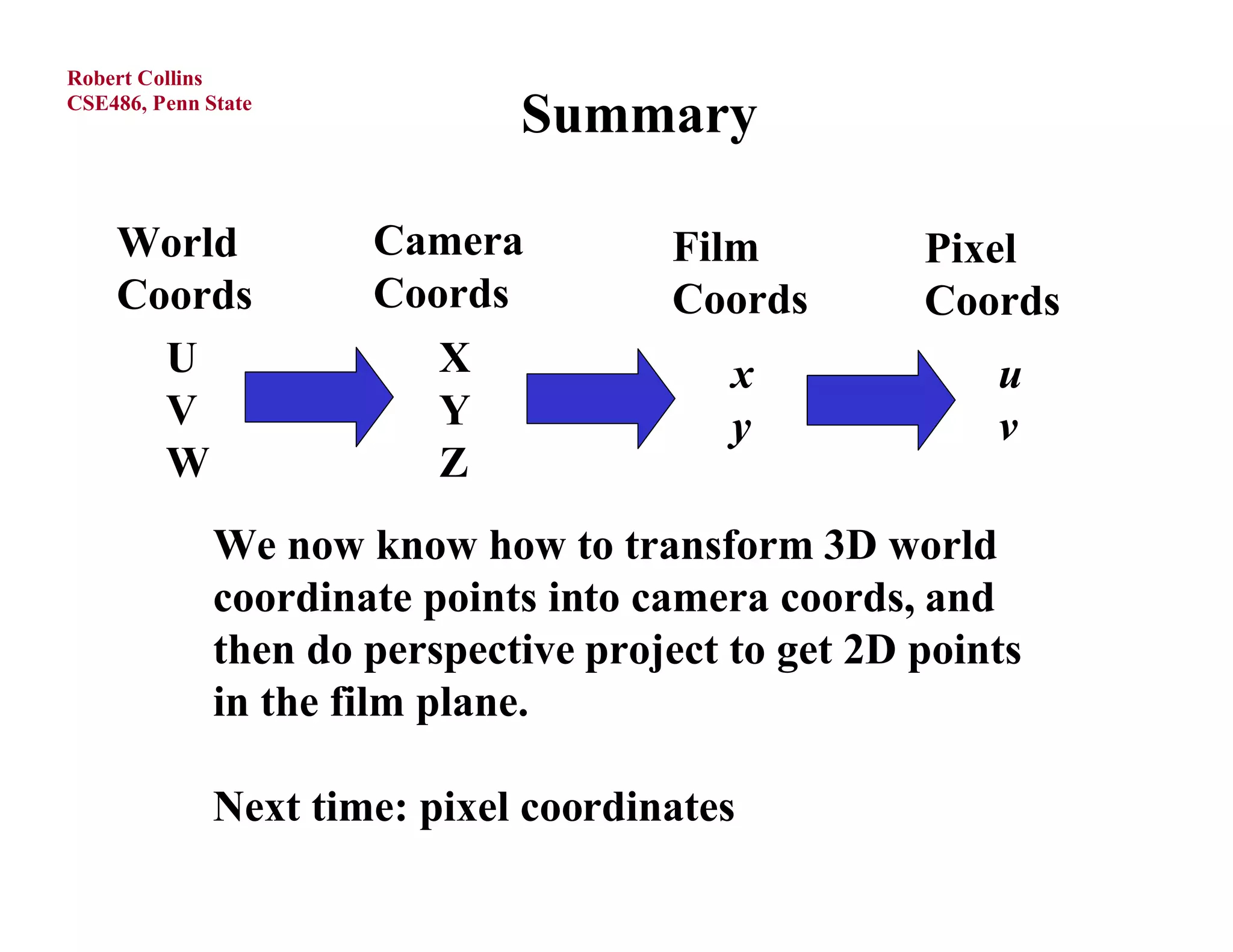
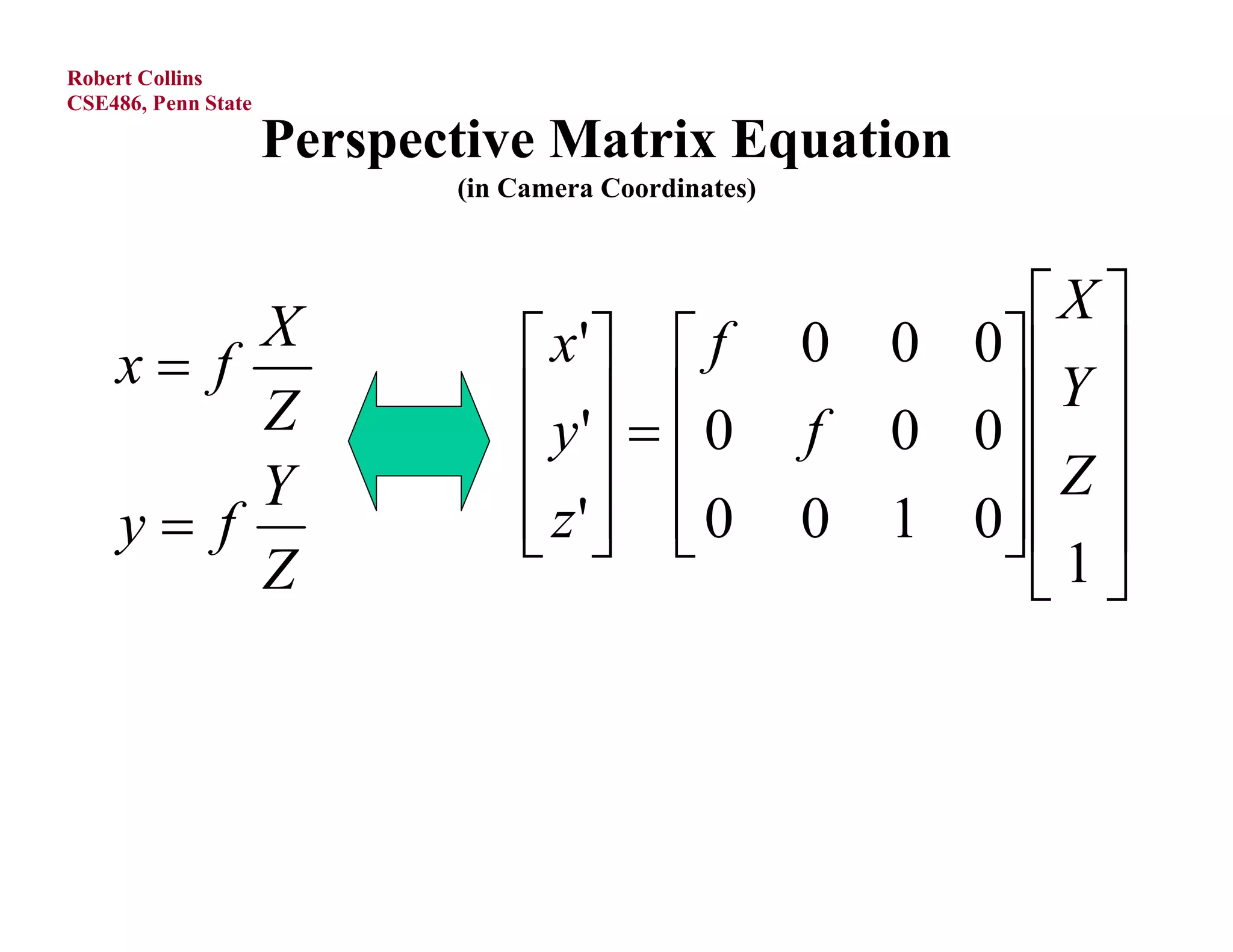
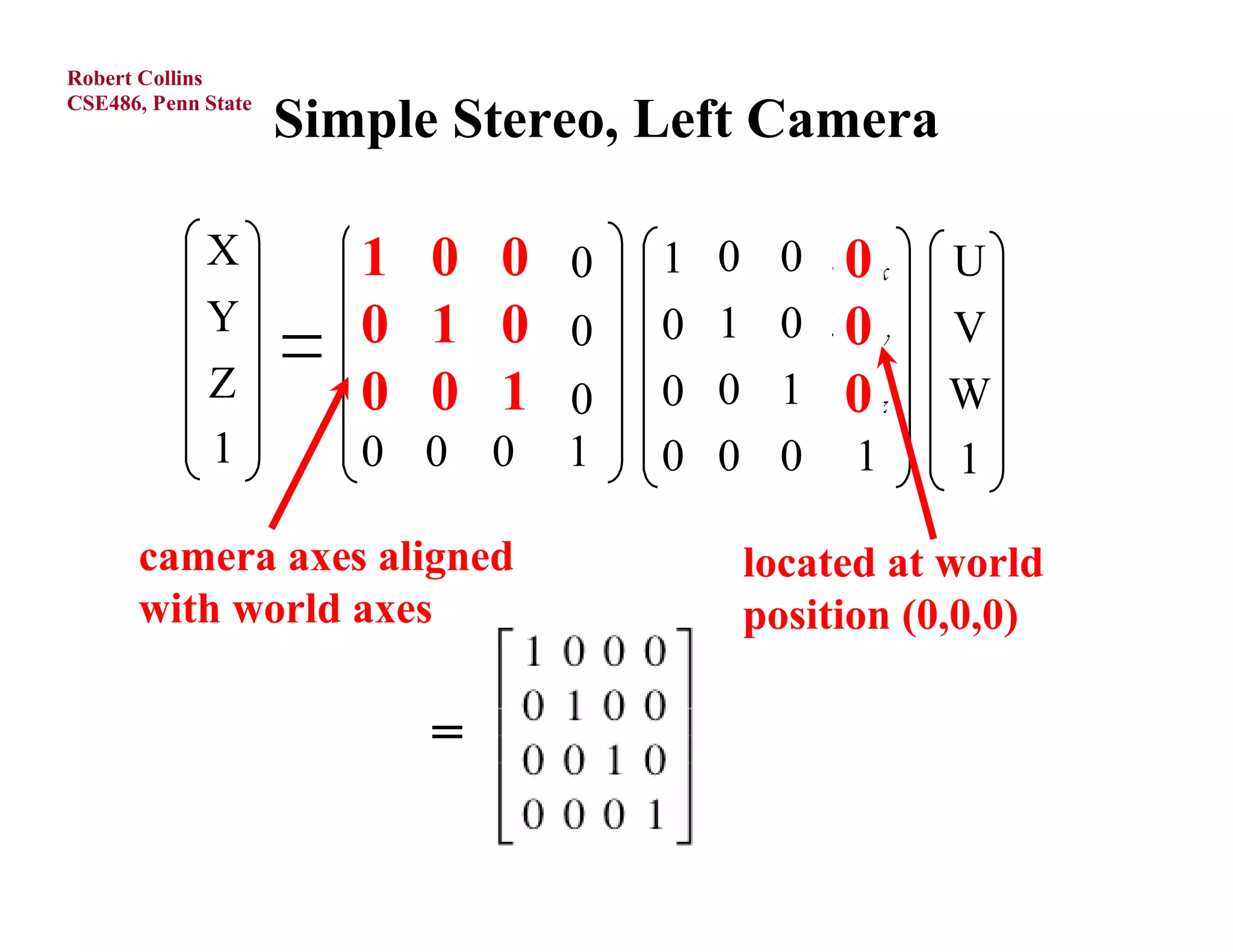
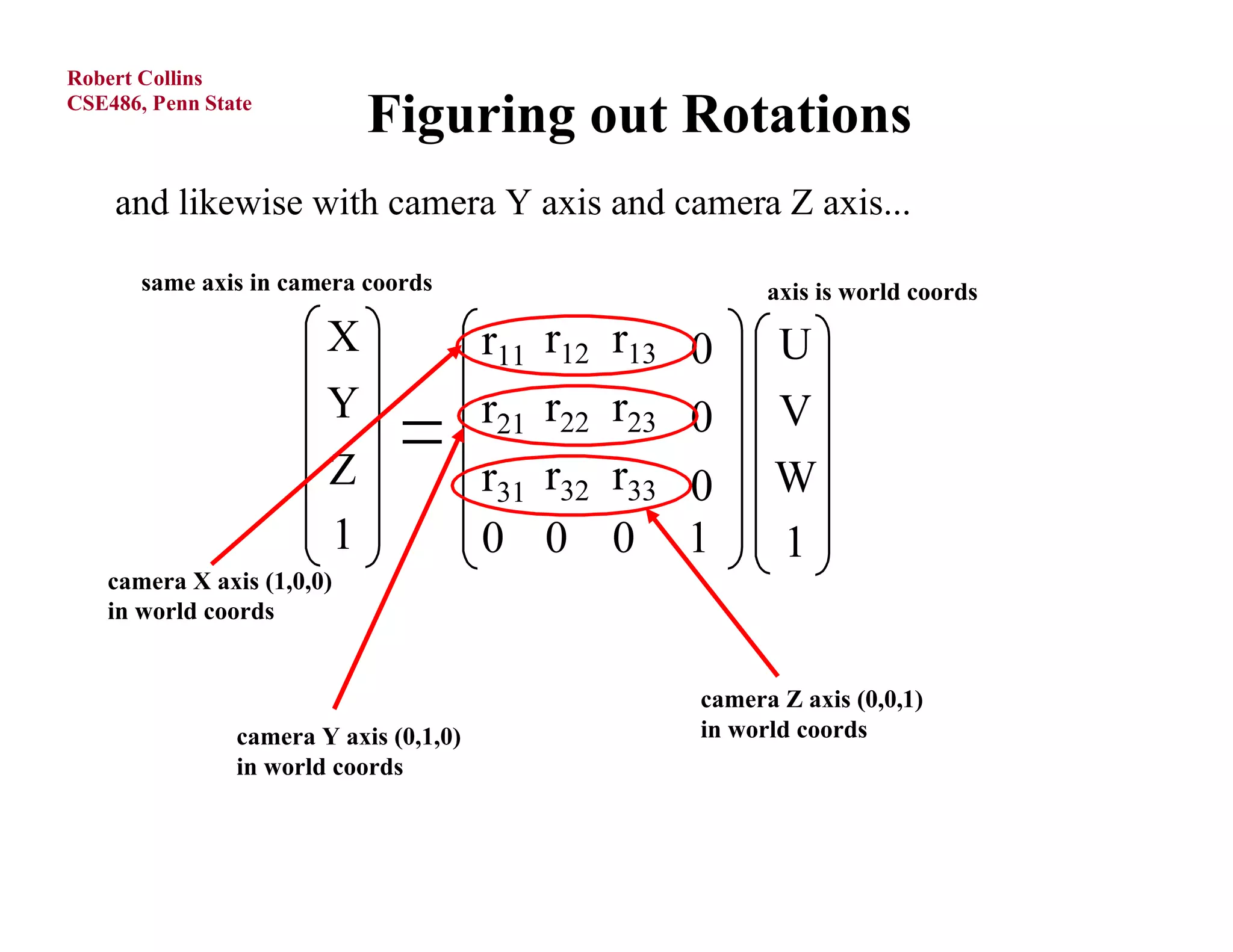
The document discusses camera projection and imaging geometry. It introduces: 1) Forward projection, which projects 3D points in a world coordinate system onto a 2D image plane using perspective projection. 2) Homogeneous coordinates, which represent 2D image points with an extra "fictitious" coordinate to write projection mathematically as a matrix equation. 3) The perspective projection matrix, which models the transformation from 3D camera coordinates to 2D image coordinates using focal length and the perspective divide.

1. Robert Collins
CSE486, Penn State
Lecture 12:
Camera Projection
Reading: T&V Section 2.4

2. Robert Collins
CSE486, Penn State
Imaging Geometry
W
Object of Interest
in World Coordinate
System (U,V,W)
V
U

3. Robert Collins
CSE486, Penn State
Imaging Geometry
Camera Coordinate
Y System (X,Y,Z).
X Z
• Z is optic axis
f • Image plane located f units
out along optic axis
• f is called focal length

4. Robert Collins
CSE486, Penn State
Imaging Geometry
W
Y y
X Z x
V
U
Forward Projection onto image plane.
3D (X,Y,Z) projected to 2D (x,y)

5. Robert Collins
CSE486, Penn State
Imaging Geometry
W
Y y
X Z x
V
u U
v Our image gets digitized
into pixel coordinates (u,v)

6. Robert Collins
CSE486, Penn State
Imaging Geometry
Camera Image (film) World
Coordinates Coordinates W
Coordinates
Y y
X Z x
V
u U
v Pixel
Coordinates

7. Robert Collins
CSE486, Penn State
Forward Projection
World Camera Film Pixel
Coords Coords Coords Coords
U X x u
V Y y v
W Z
We want a mathematical model to describe
how 3D World points get projected into 2D
Pixel coordinates.
Our goal: describe this sequence of
transformations by a big matrix equation!

8. Robert Collins
CSE486, Penn State
Backward Projection
World Camera Film Pixel
Coords Coords Coords Coords
U X x u
V Y y v
W Z
Note, much of vision concerns trying to
derive backward projection equations to
recover 3D scene structure from images
(via stereo or motion)
But first, we have to understand forward projection…

9. Robert Collins
CSE486, Penn State
Forward Projection
World Camera Film Pixel
Coords Coords Coords Coords
U X x u
V Y y v
W Z
3D-to-2D Projection
• perspective projection
We will start here in the middle, since we’ve already
talked about this when discussing stereo.

10. Robert Collins
CSE486, Penn State
Basic Perspective Projection
Scene Point Perspective Projection Eqns
P = (X,Y,Z)
X
Image Point y x f
Y
p = (x,y,f) X Y
Z
x Y
Z
y
y f
x
X
f Z
Z
O
O.Camps, PSU

11. Robert Collins
CSE486, Penn State
Basic Perspective Projection
Scene Point Perspective Projection Eqns
P = (X,Y,Z)
X
Image Point y x f
Y
p = (x,y,f) X Y
Z
x Y
Z
y
y f
x
X
f Z
Z derived via similar
O
triangles rule
x X
f
Z
O.Camps, PSU

12. Robert Collins
CSE486, Penn State
Basic Perspective Projection
Scene Point Perspective Projection Eqns
P = (X,Y,Z)
X
Image Point y x f
Y
p = (x,y,f) X Y
Z
x Y
Z
y
y f
x
X
f Z
Z derived via similar
O
triangles rule
X Y
y
x
f f
Z Z
O.Camps, PSU

13. Robert Collins
CSE486, Penn State
Basic Perspective Projection
Scene Point Perspective Projection Eqns
P = (X,Y,Z)
X
Image Point y x f
Y
p = (x,y,f) X Y
Z
x Y
Z
y
y f
x
X
f Z
Z
O
So how do we represent this as a matrix equation?
We need to introduce homogeneous coordinates.
O.Camps, PSU

14. Robert Collins
CSE486, Penn State
Homogeneous Coordinates
Represent a 2D point (x,y) by a 3D point (x’,y’,z’) by
adding a “fictitious” third coordinate.
By convention, we specify that given (x’,y’,z’) we can
recover the 2D point (x,y) as
x' y'
x y
z' z'
Note: (x,y) = (x,y,1) = (2x, 2y, 2) = (k x, ky, k)
for any nonzero k (can be negative as well as positive)

15. Robert Collins
CSE486, Penn State
Perspective Matrix Equation
(in Camera Coordinates)
X X 
x f  x'  f 0 0 0  
Z  y '   0 f Y 
0 0
Y    Z 
y f  z'  0
   0 1 0  
 1
Z  

16. Robert Collins
CSE486, Penn State
Forward Projection
World Camera Film Pixel
Coords Coords Coords Coords
U X x u
V Y y v
W Z
Rigid Transformation (rotation+translation)
between world and camera coordinate systems

17. Robert Collins
World to Camera Transformation
CSE486, Penn State
PC PW
W
Y
X
U
Z V
Avoid confusion: Pw and Pc are not two different
points. They are the same physical point, described
in two different coordinate systems.

18. Robert Collins
World to Camera Transformation
CSE486, Penn State
PC PW
W
Y
X
U
R Z V
C
Rotate to Translate by - C
align axes (align origins)
P C = R ( PW - C )

19. Robert Collins
Matrix Form, Homogeneous Coords
CSE486, Penn State
P C = R ( PW - C )
X r11 r12 r13  1 0 0  cx U
Y r21 r22 r23  0 1 0  cy V
Z r31 r32 r33  0 0 1  cz W
1 0 0 0 1 0 0 0 1 1

20. Robert Collins
CSE486, Penn State
Example: Simple Stereo System
Y Z
(X,Y,Z)
z
left y
camera
located at ( , )
z
(0,0,0) y ( , )
x right
camera
Tx located at
x (Tx,0,0)
X
Left camera located at world origin (0,0,0)
and camera axes aligned with world coord axes.

21. Robert Collins
CSE486, Penn State
Simple Stereo, Left Camera
X 1
r11 r12 r0 
0 13 1 0 0
0  cx U
Y 0
r21 r22 r0 
1 23 0 1 0
0  cy V
Z 0 r32 r1 
0 33
r31 0 0 0
1  cz W
1 0 0 0 1 0 0 0 1 1
camera axes aligned located at world
with world axes position (0,0,0)
=

22. Robert Collins
Simple Stereo Projection Equations
CSE486, Penn State
Left camera

23. Robert Collins
CSE486, Penn State
Example: Simple Stereo System
Y Z
(X,Y,Z)
z
left y
camera
located at ( , )
z
(0,0,0) y ( , )
x right
camera
Tx located at
x (Tx,0,0)
X
Right camera located at world location (Tx,0,0)
and camera axes aligned with world coord axes.

24. Robert Collins
CSE486, Penn State
Simple Stereo, Right Camera
X 1
r11 r12 r0 
0 13 1 0 0 -Tx
 cx U
Y 0
r21 r22 r0 
1 23 0 1 0
0  cy V
Z 0 r32 r1 
0 33
r31 0 0 0
1  cz W
1 0 0 0 1 0 0 0 1 1
camera axes aligned located at world
with world axes position (Tx,0,0)
=

25. Robert Collins
Simple Stereo Projection Equations
CSE486, Penn State
Left camera
Right camera

26. Robert Collins
CSE486, Penn State
Bob’s sure-fire way(s) to
figure out the rotation
X r11 r12 r13  1 0 0  cx U
Y r21 r22 r23  0forget about  cy
1 0 this V
while thinking
Z r31 r32 r33  0about rotationscz
0 1  W
1 0 0 0 1 0 0 0 1 1
PC = R P W
This equation says how vectors in the world coordinate
system (including the coordinate axes) get transformed
into the camera coordinate system.

27. Robert Collins
CSE486, Penn State
Figuring out Rotations
X r11 r12 r13  U
Y r21 r22 r23  V PC = R P W
Z r31 r32 r33  W
1 0 0 0 1 1
what if world x axis (1,0,0) corresponds to camera axis (a,b,c)?
X
a r11 r12 r13  U
1 X
a ra r12 r13
11  U
1
Y
b r21 r22 r23  V
0 Y
b rb r22 r23
21  V
0
Z
c r31 r32 r33  0
W Z
c rc r32 r33  0
W
31
1 0 0 0 1 1 1 0 0 0 1 1
we can immediately write down the first column of R!

28. Robert Collins
CSE486, Penn State
Figuring out Rotations
and likewise with world Y axis and world Z axis...
same axis in camera coords axis is world coords
X r11 r12 r13  U
Y r21 r22 r23  V
Z r31 r32 r33  W
1 0 0 0 1 1
world X axis (1,0,0) world Z axis (0,0,1)
in camera coords in camera coords
world Y axis (0,1,0)
in camera coords

29. Robert Collins
CSE486, Penn State
Figuring out Rotations
Alternative approach: sometimes it is easier to specify
what camera X,Y,or Z axis is in world coordinates. Then
do rearrange the equation as follows.
PC = R P W R-1PC = PW RTPC = PW
r11 r21 r31  X U
r12 r22 r32  Y V
r13 r23 r33  Z W
0 0 0 1 1 1

30. Robert Collins
CSE486, Penn State
Figuring out Rotations
r11 r21 r31  X U
r12 r22 r32  Y V RTPC = PW
r13 r23 r33  Z W
0 0 0 1 1 1
what if camera X axis (1,0,0) corresponds to world axis (a,b,c)?
r11 r21 r31  X
1 U
a ra r21 r31  X
11 1 U
a
r12 r22 r32  Y
0 V
b rb r22 r32  Y
12 0 V
b
r13 r23 r33  Z
0 W
c
13
0
rc r23 r33  Z W
c
0 0 0 1 1 1 0 0 0 1 1 1
we can immediately write down the first column of RT,
(which is the first row of R).

31. Robert Collins
CSE486, Penn State
Figuring out Rotations
and likewise with camera Y axis and camera Z axis...
same axis in camera coords axis is world coords
X r11 r12 r13  U
Y r21 r22 r23  V
Z r31 r32 r33  W
1 0 0 0 1 1
camera X axis (1,0,0)
in world coords
camera Z axis (0,0,1)
camera Y axis (0,1,0) in world coords
in world coords

32. Robert Collins
CSE486, Penn State
Example
y
z
x
0 0 1 0 -1 0
Rtrain 0 -1 0 Rfly 0 0 1
1 0 0 -1 0 0

33. Robert Collins
CSE486, Penn State Note: External Parameters
also often written as R,T
X r11 r12 r13  1 0 0  cx U
Y r21 r22 r23  0 1 0  cy V
Z r31 r32 r33  0 0 1  cz W
1 0 0 0 1 0 0 0 1 1
R ( PW - C ) r11 r12 r13 tx
r21 r22 r23 ty
= R PW - R C
r31 r32 r33 tz
= R PW + T 0 0 0 1

34. Robert Collins
CSE486, Penn State
Summary
World Camera Film Pixel
Coords Coords Coords Coords
U X x u
V Y y v
W Z
We now know how to transform 3D world
coordinate points into camera coords, and
then do perspective project to get 2D points
in the film plane.
Next time: pixel coordinates