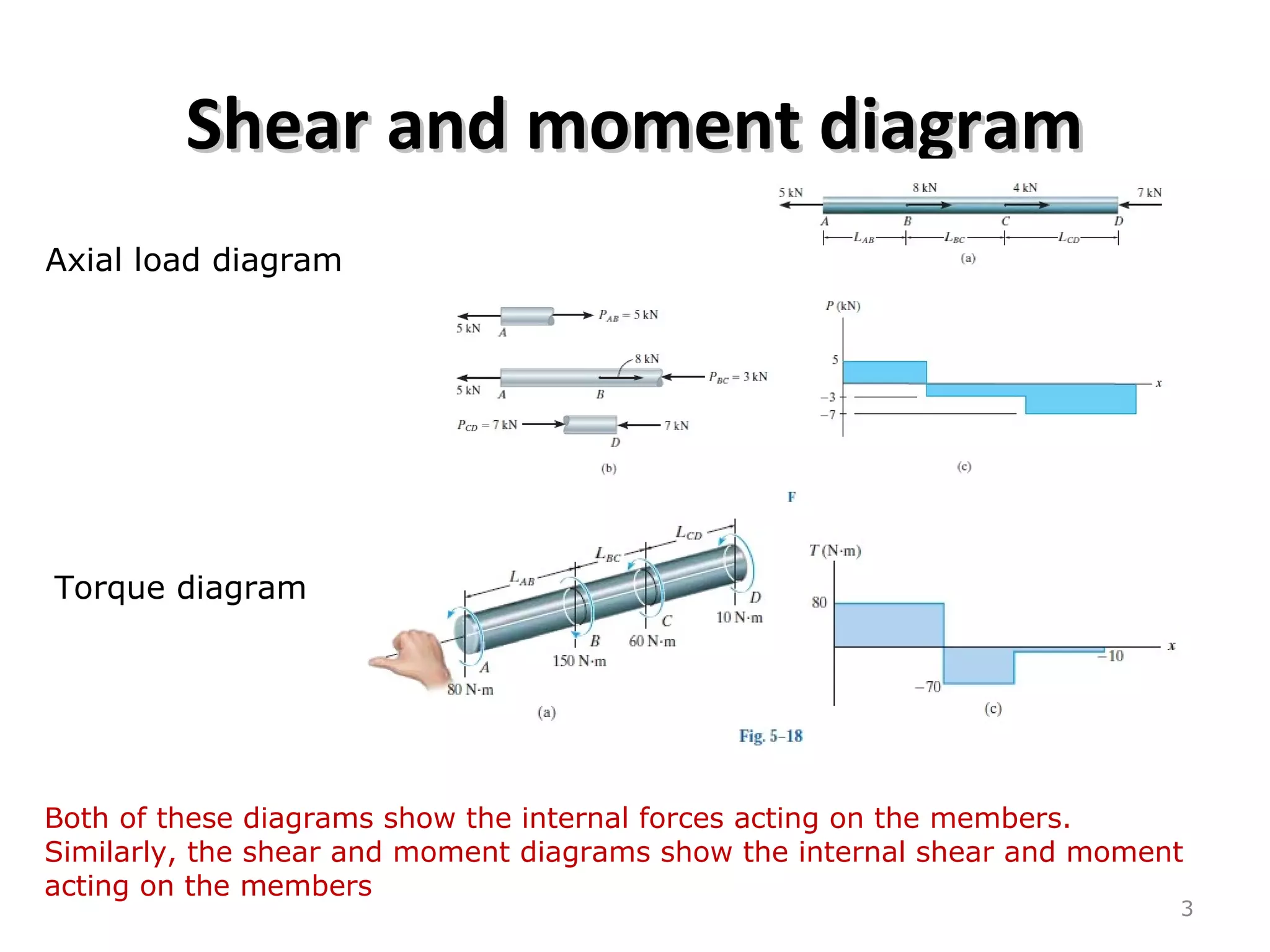
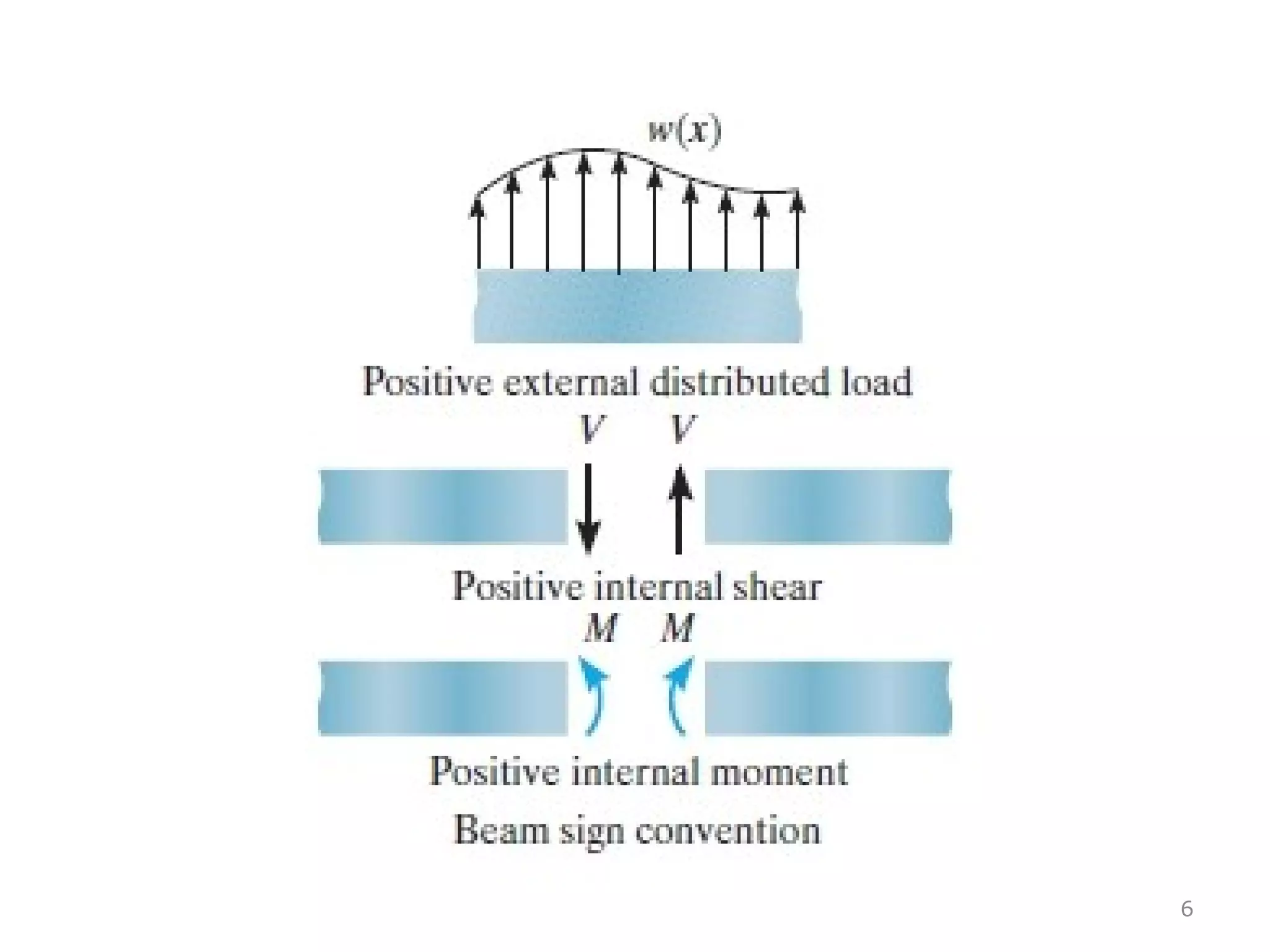
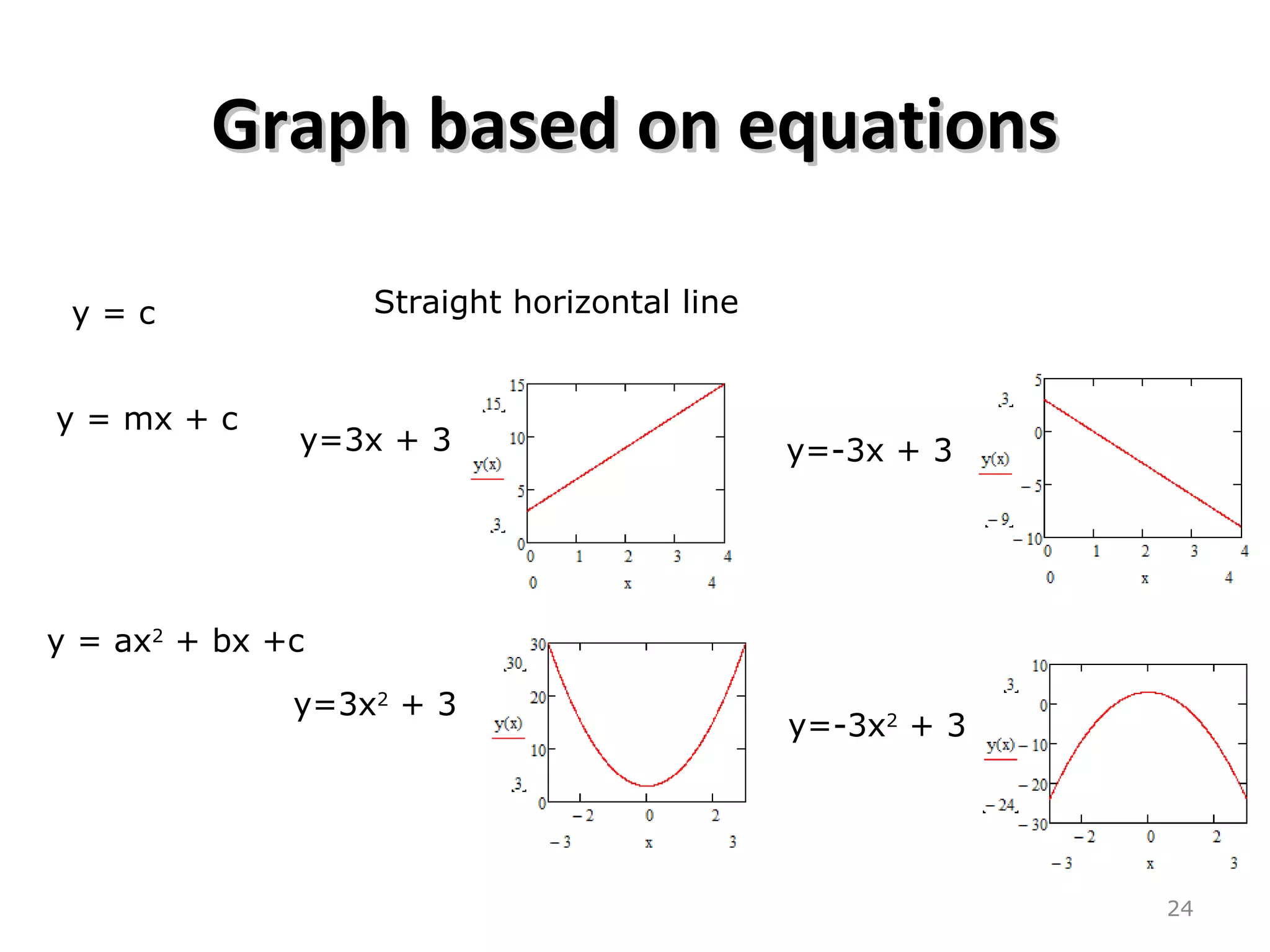
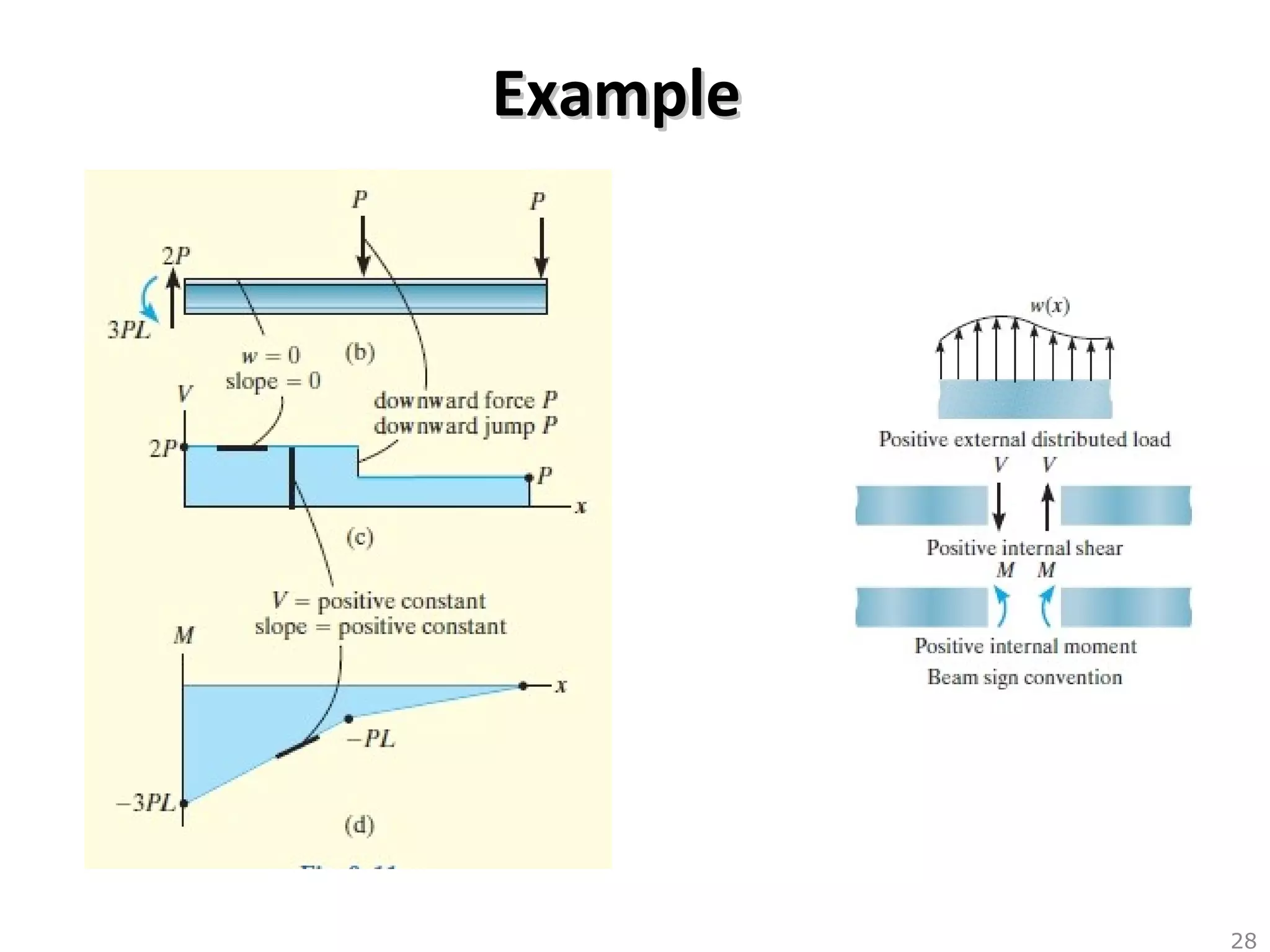
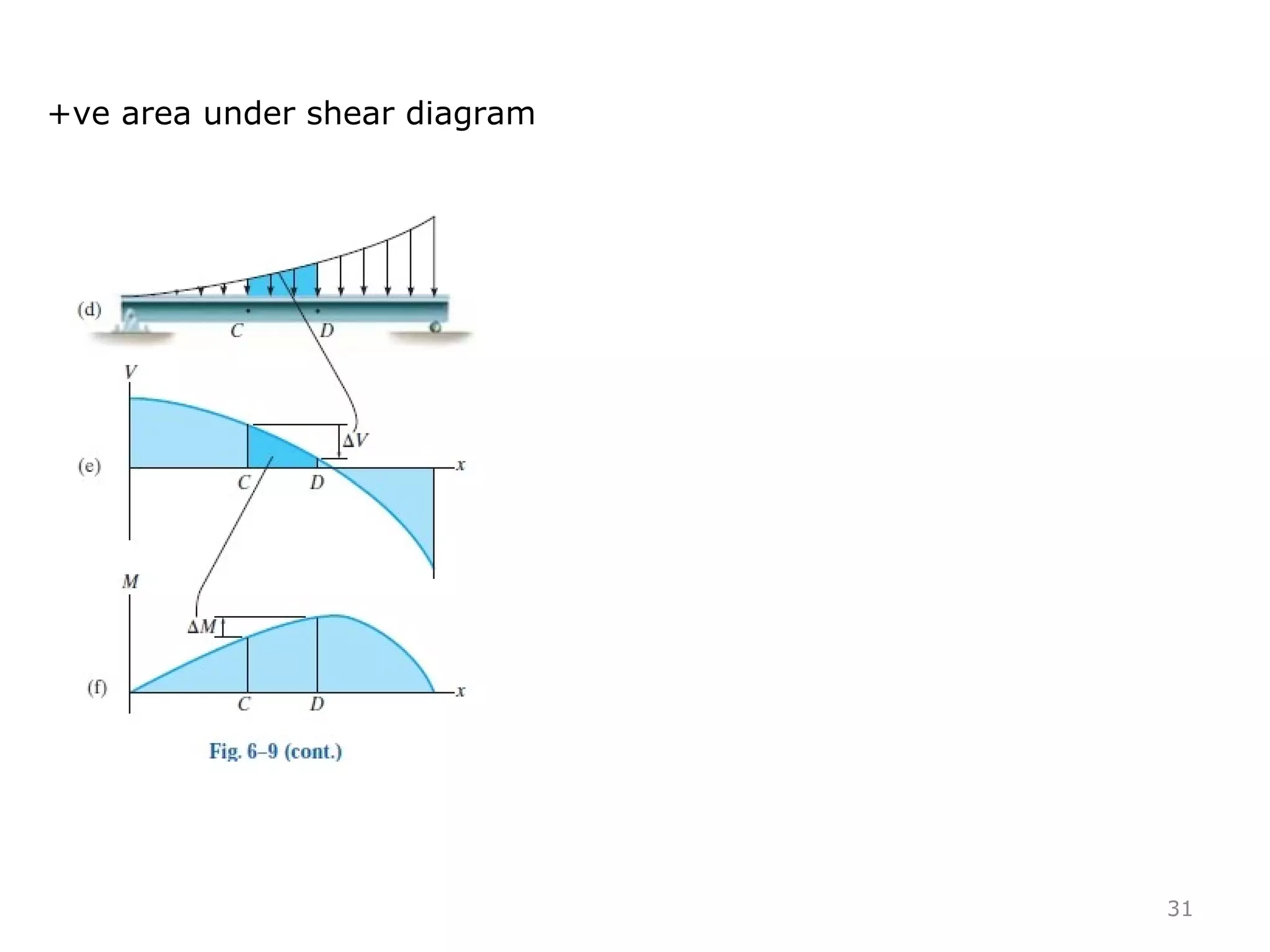
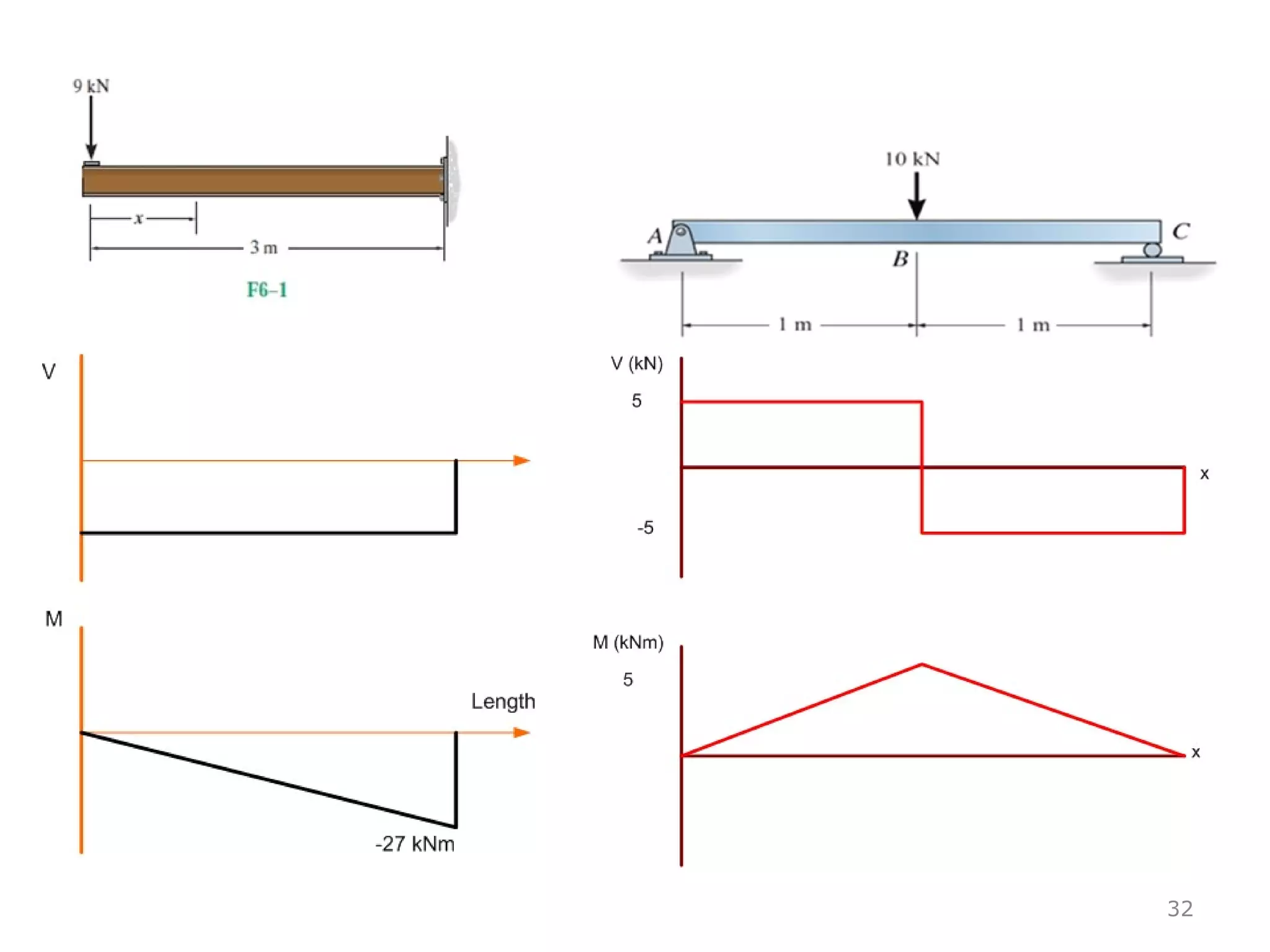
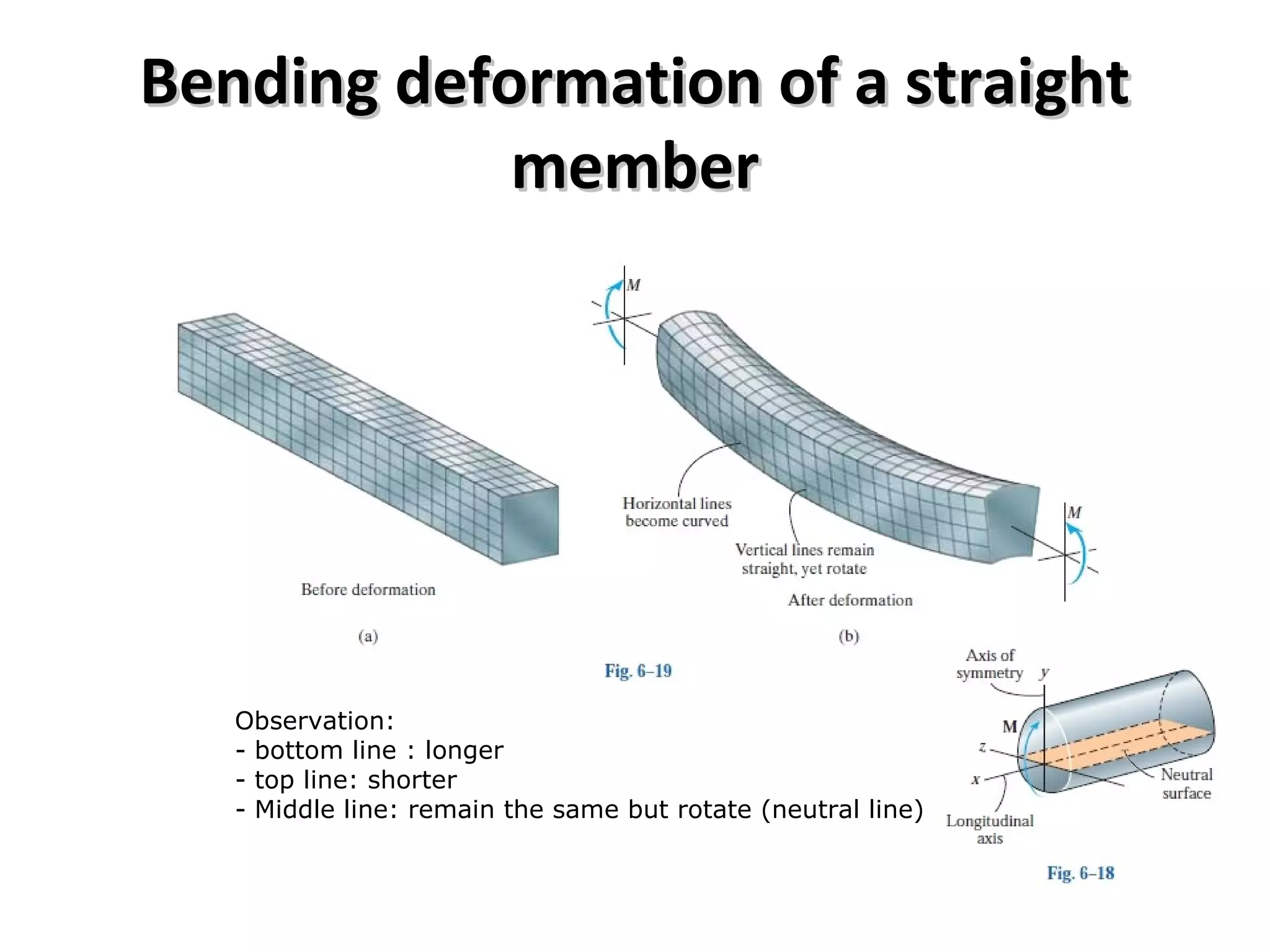
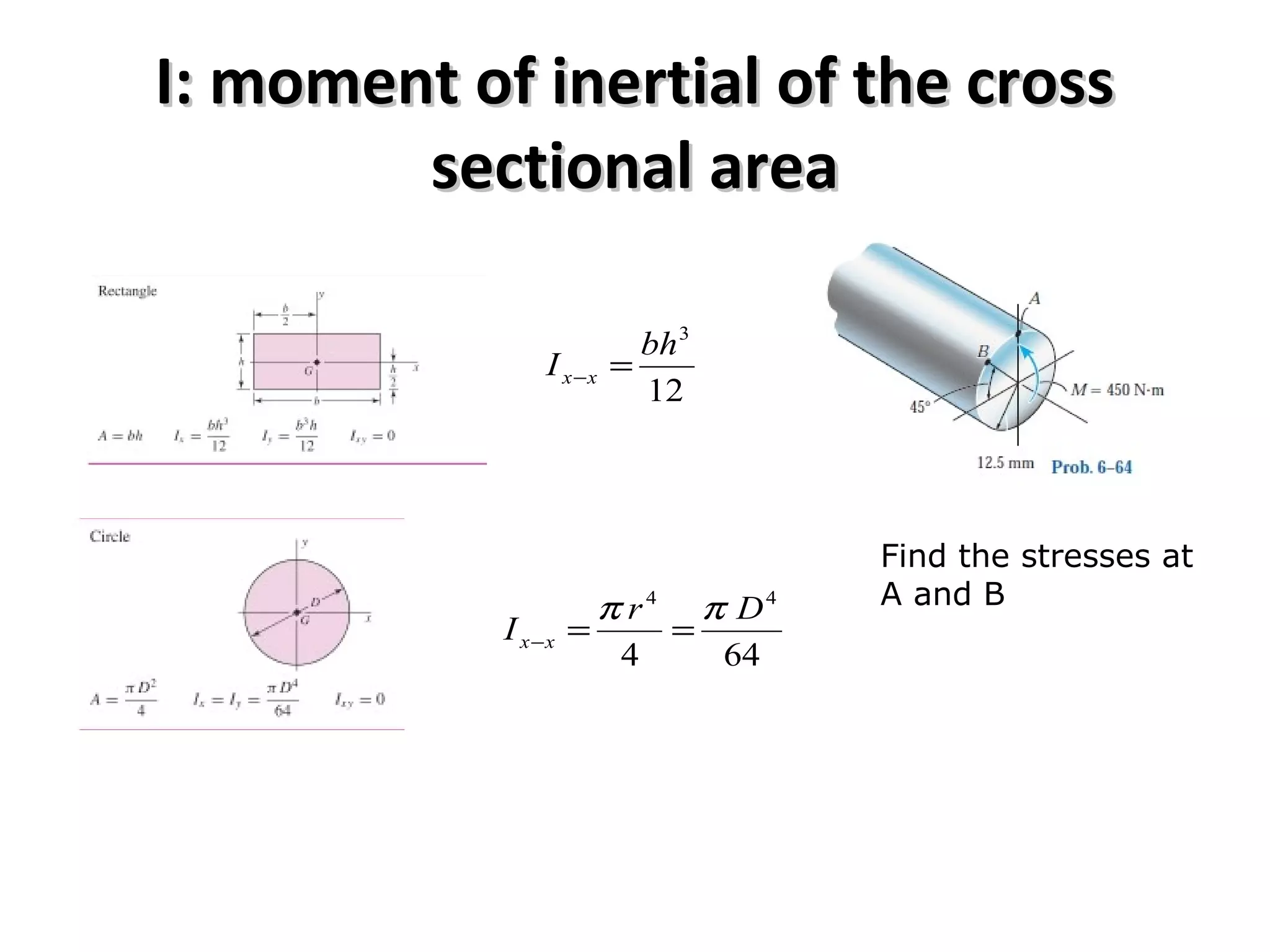
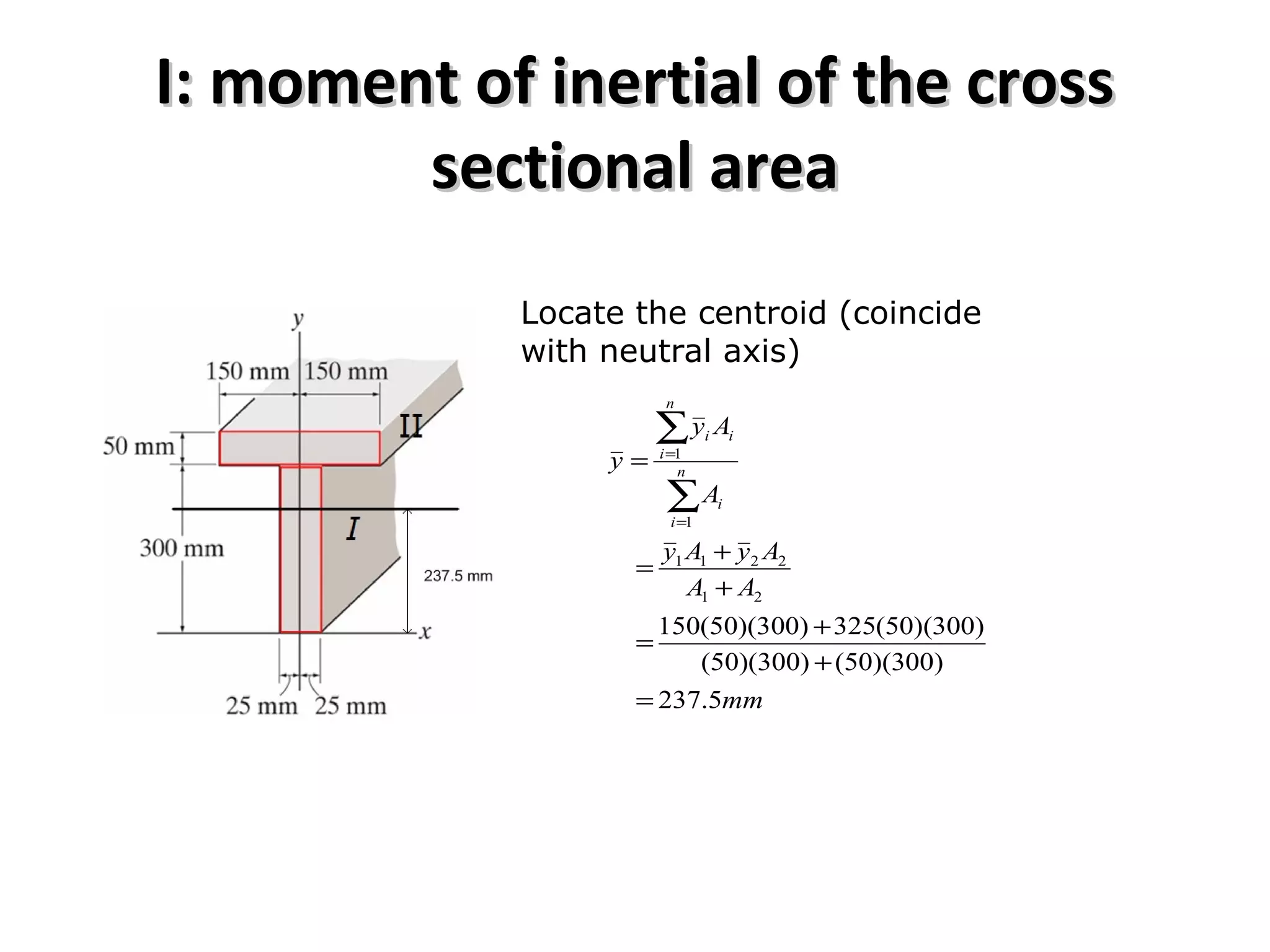
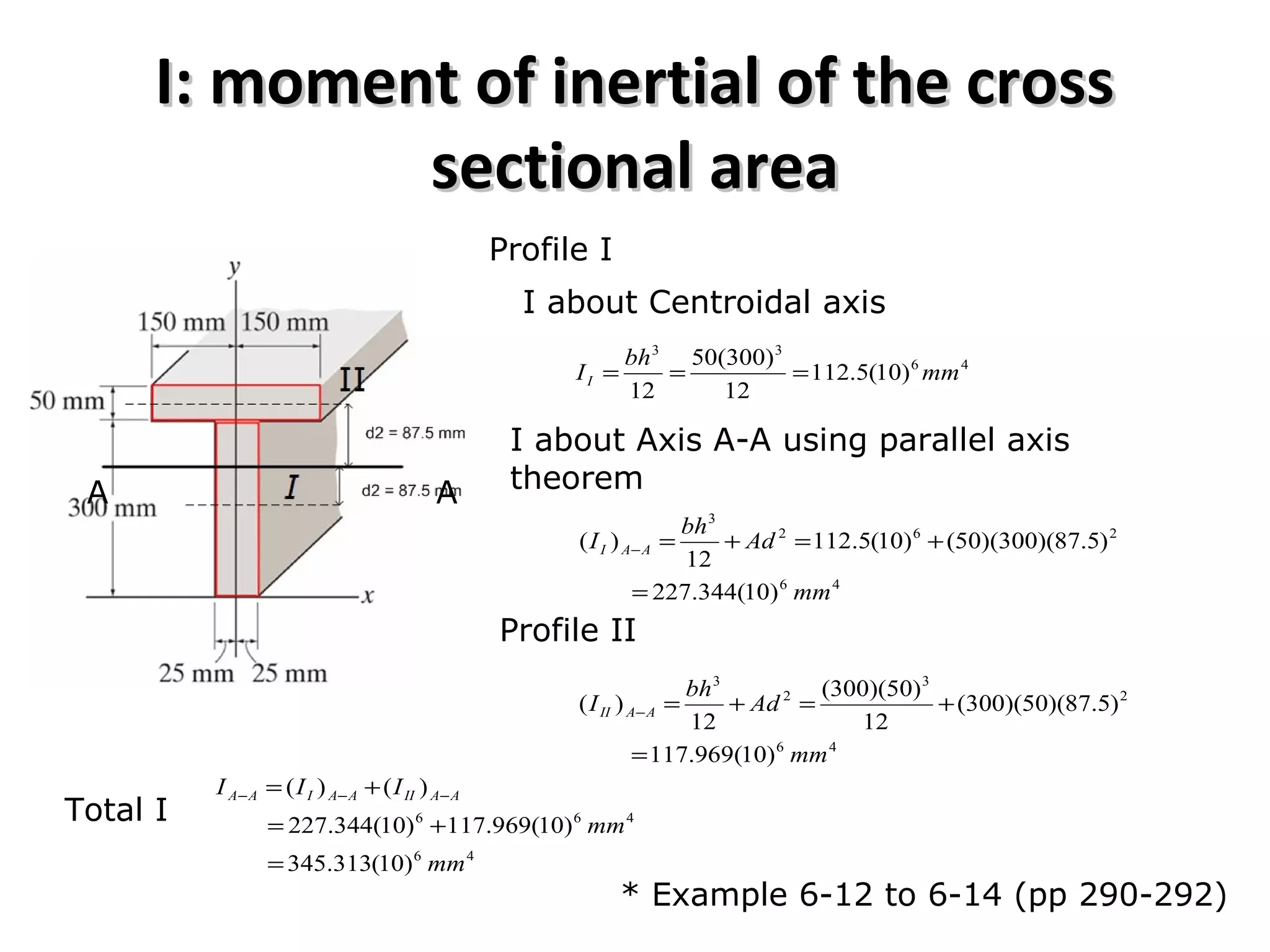
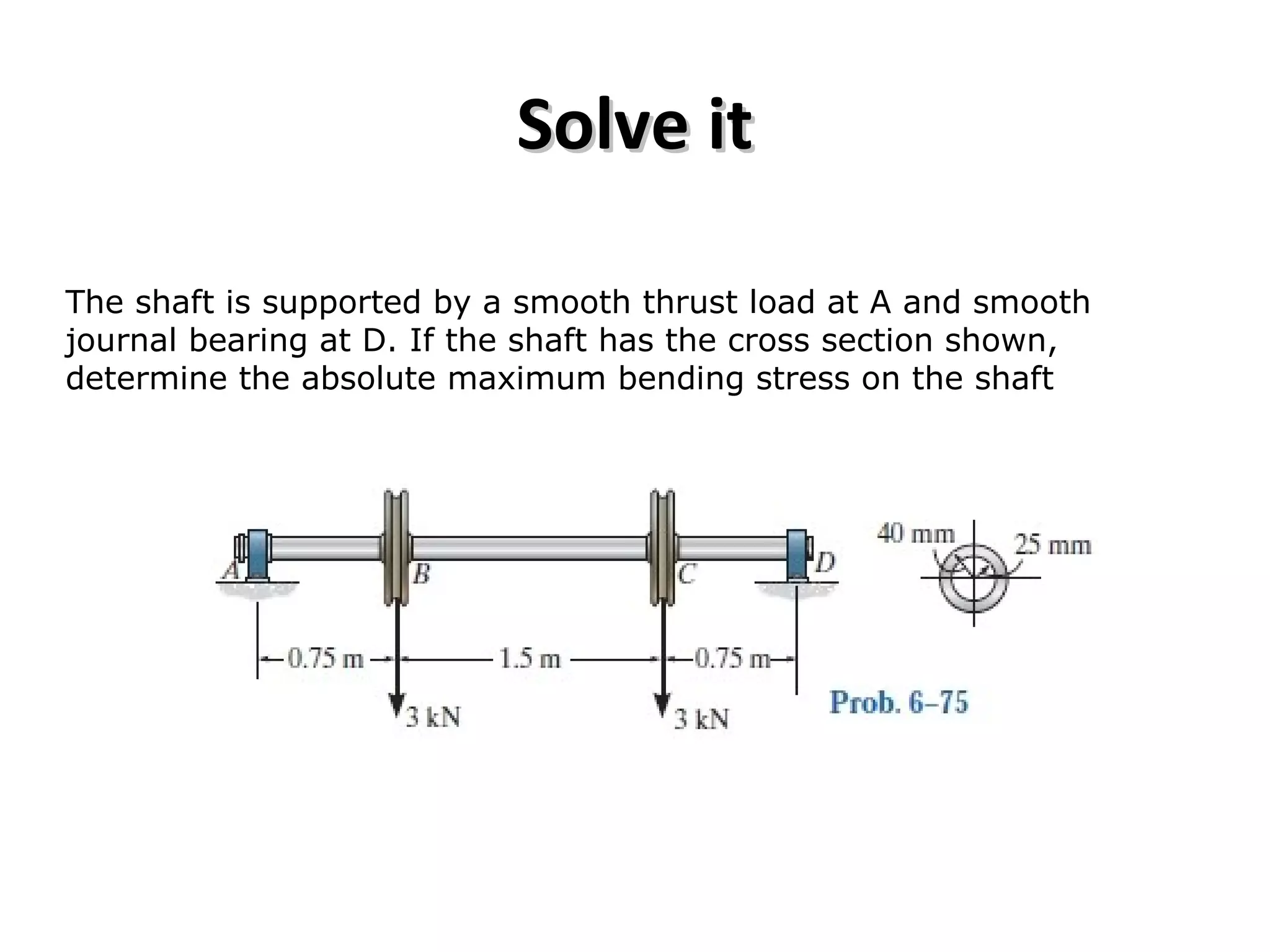
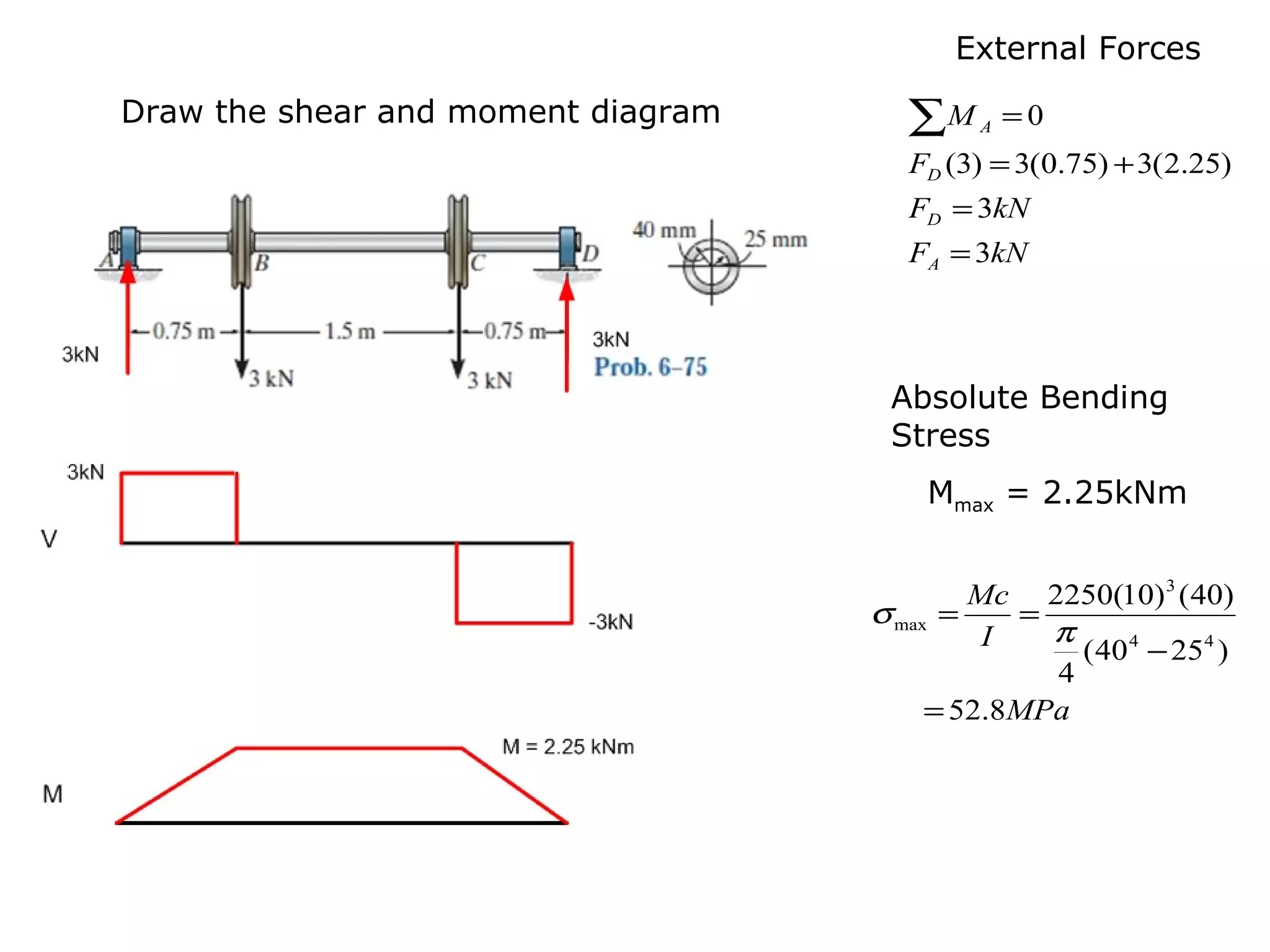
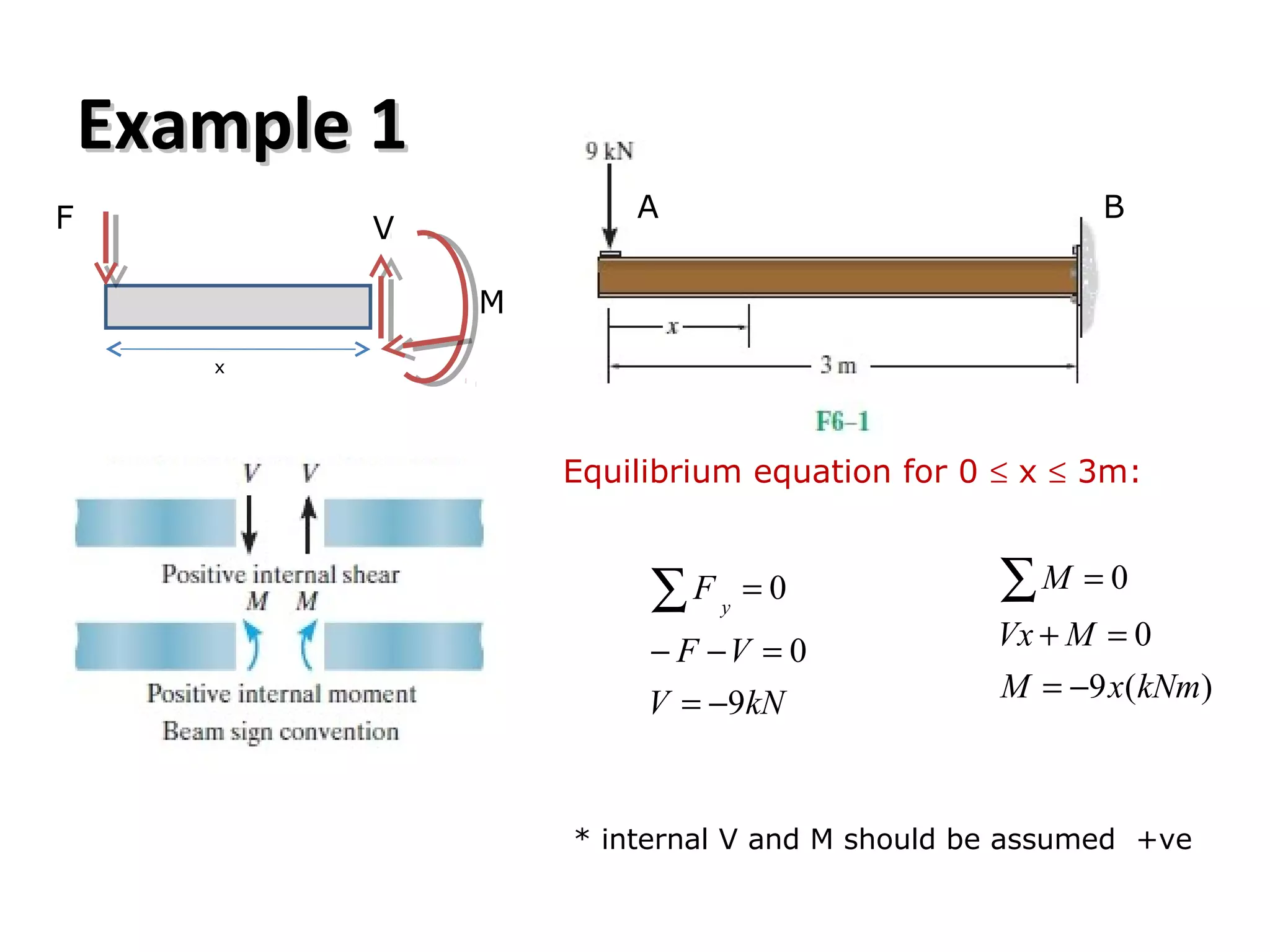
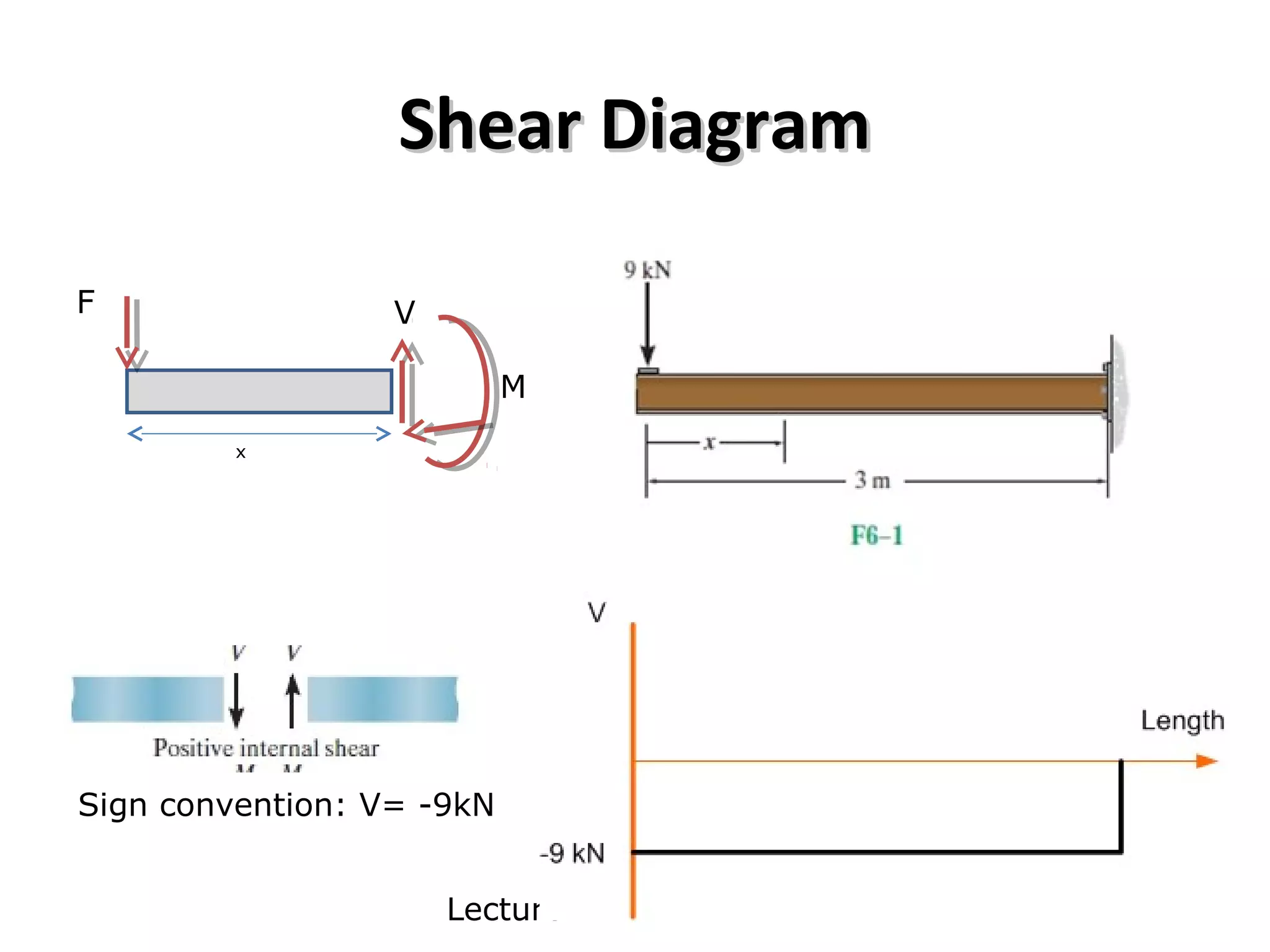
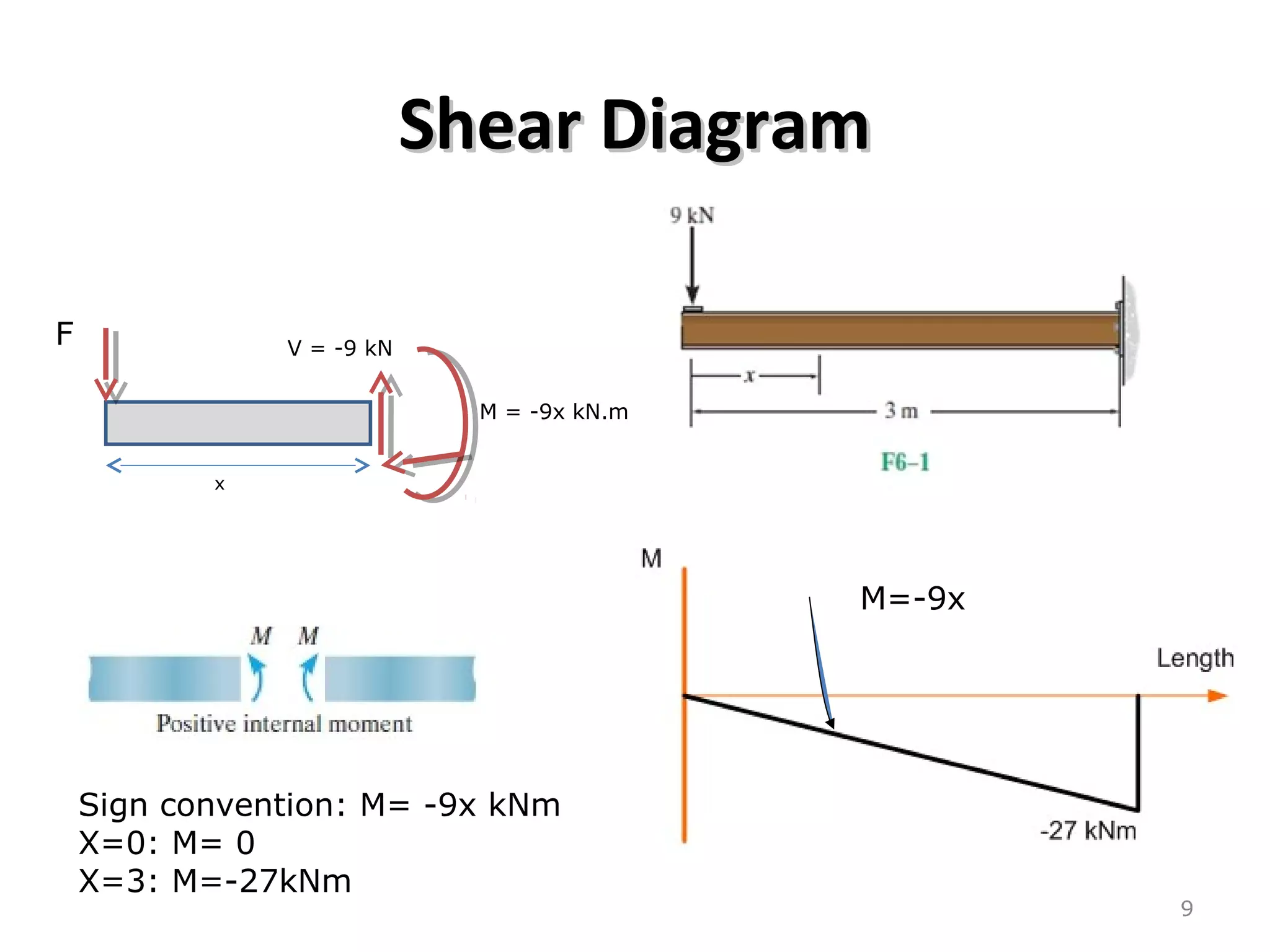
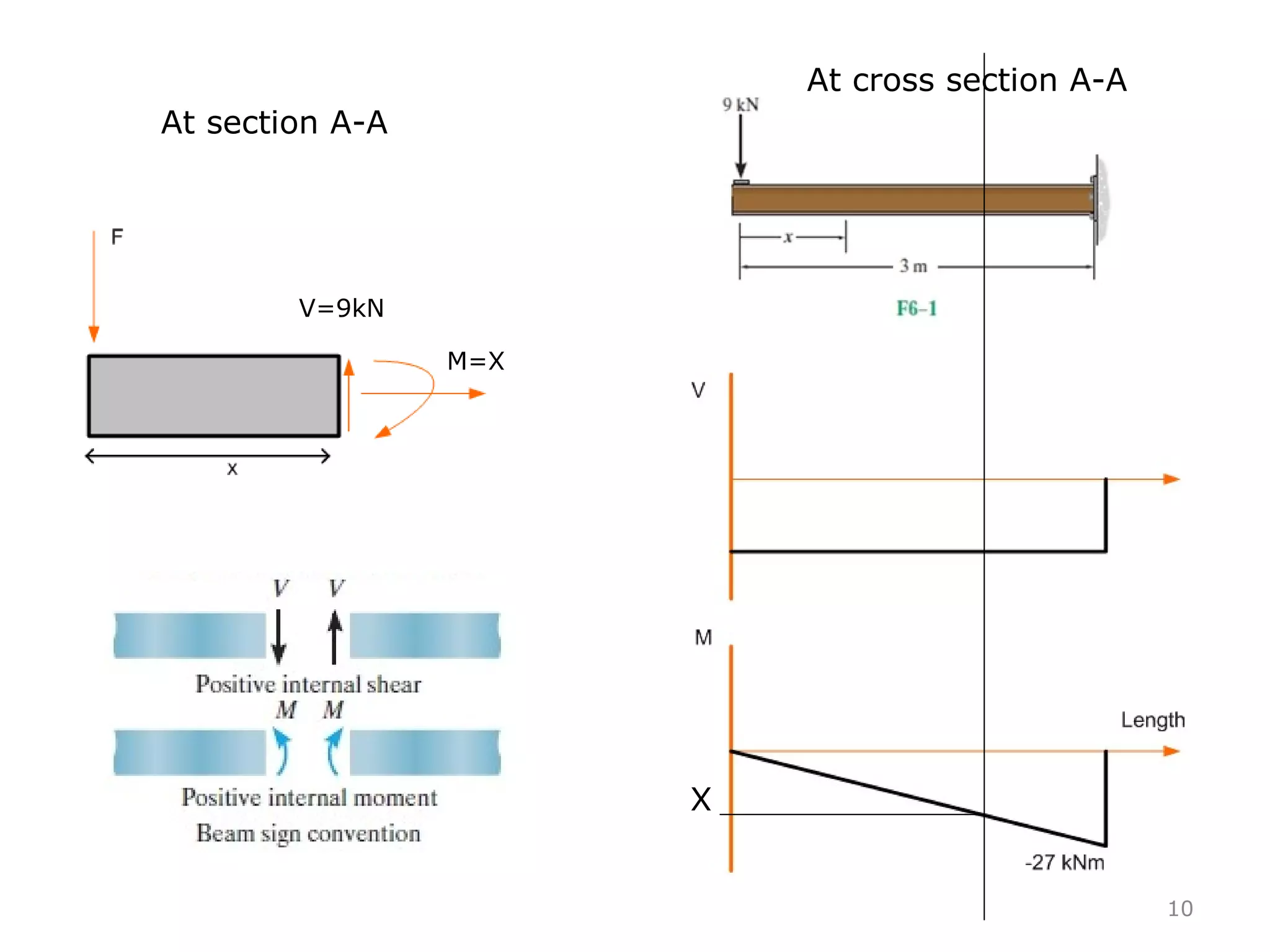
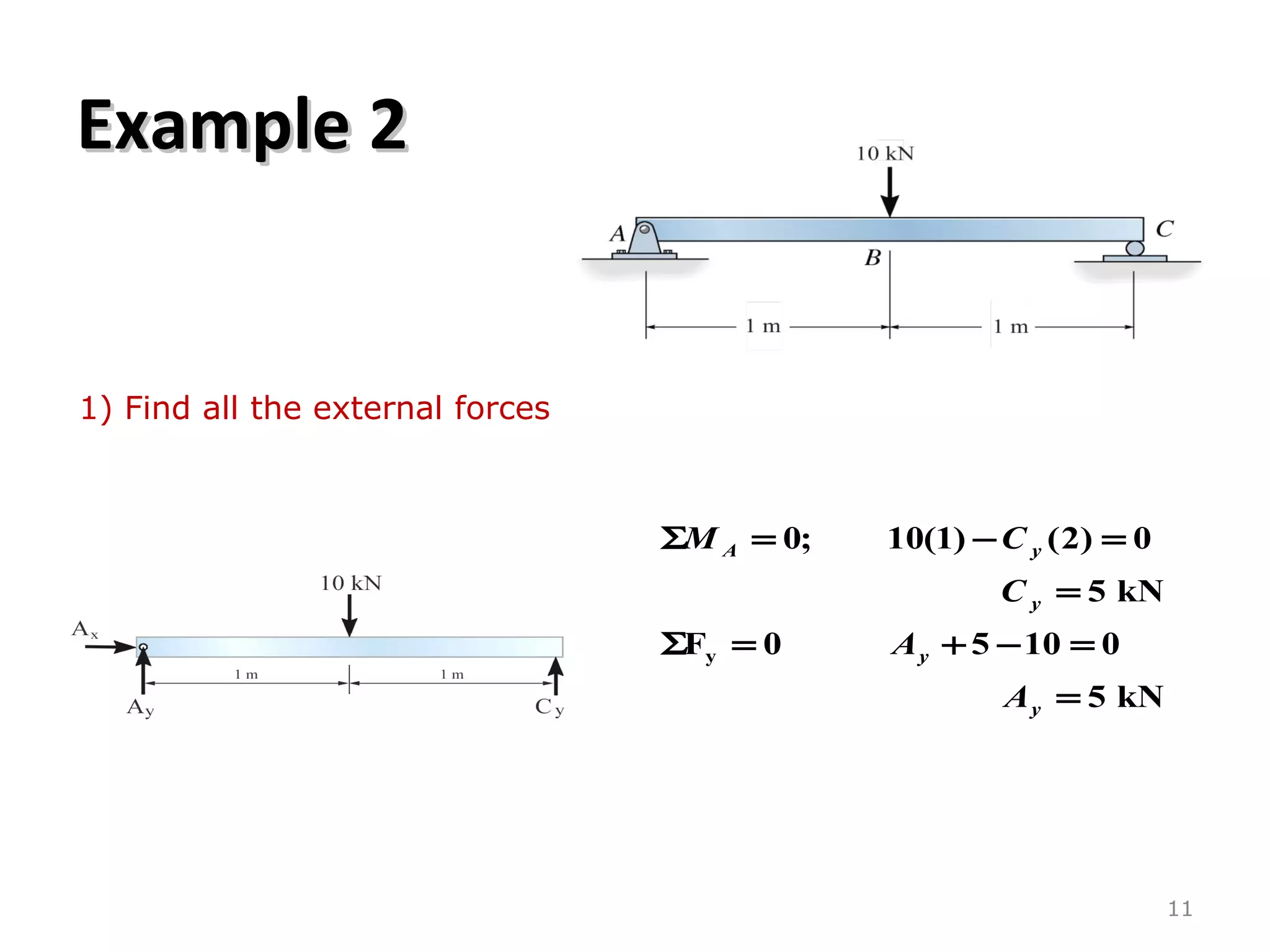
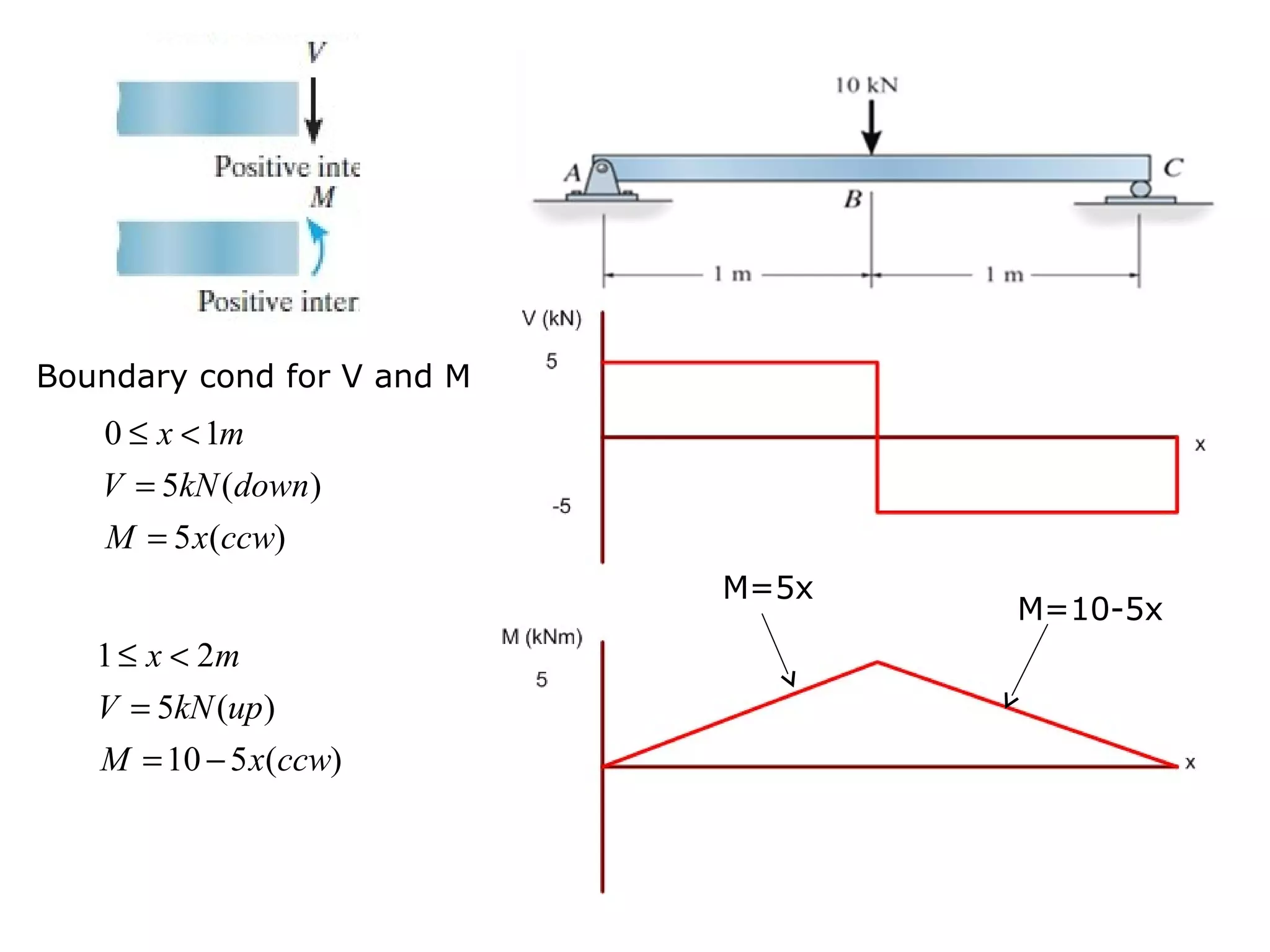
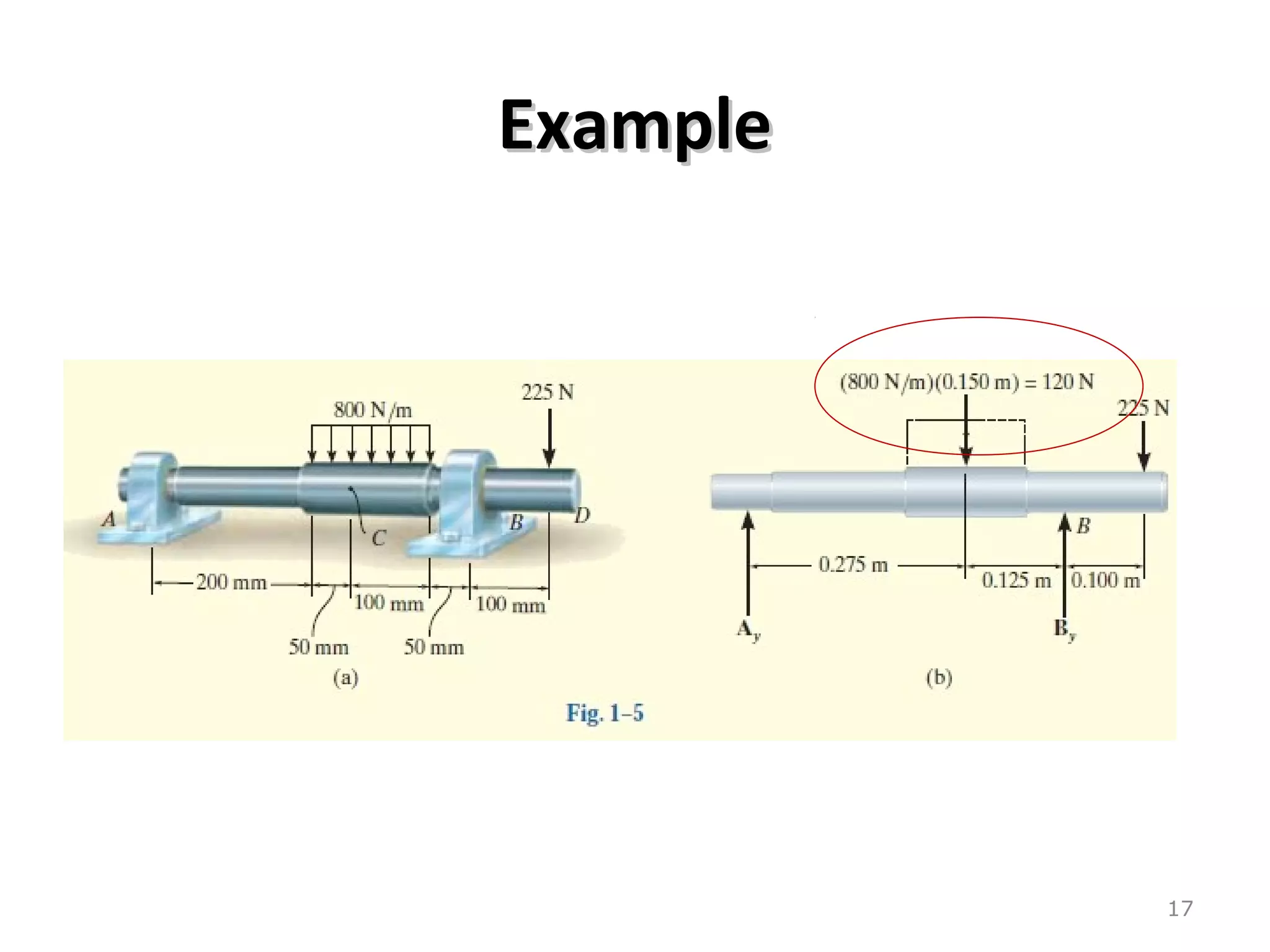
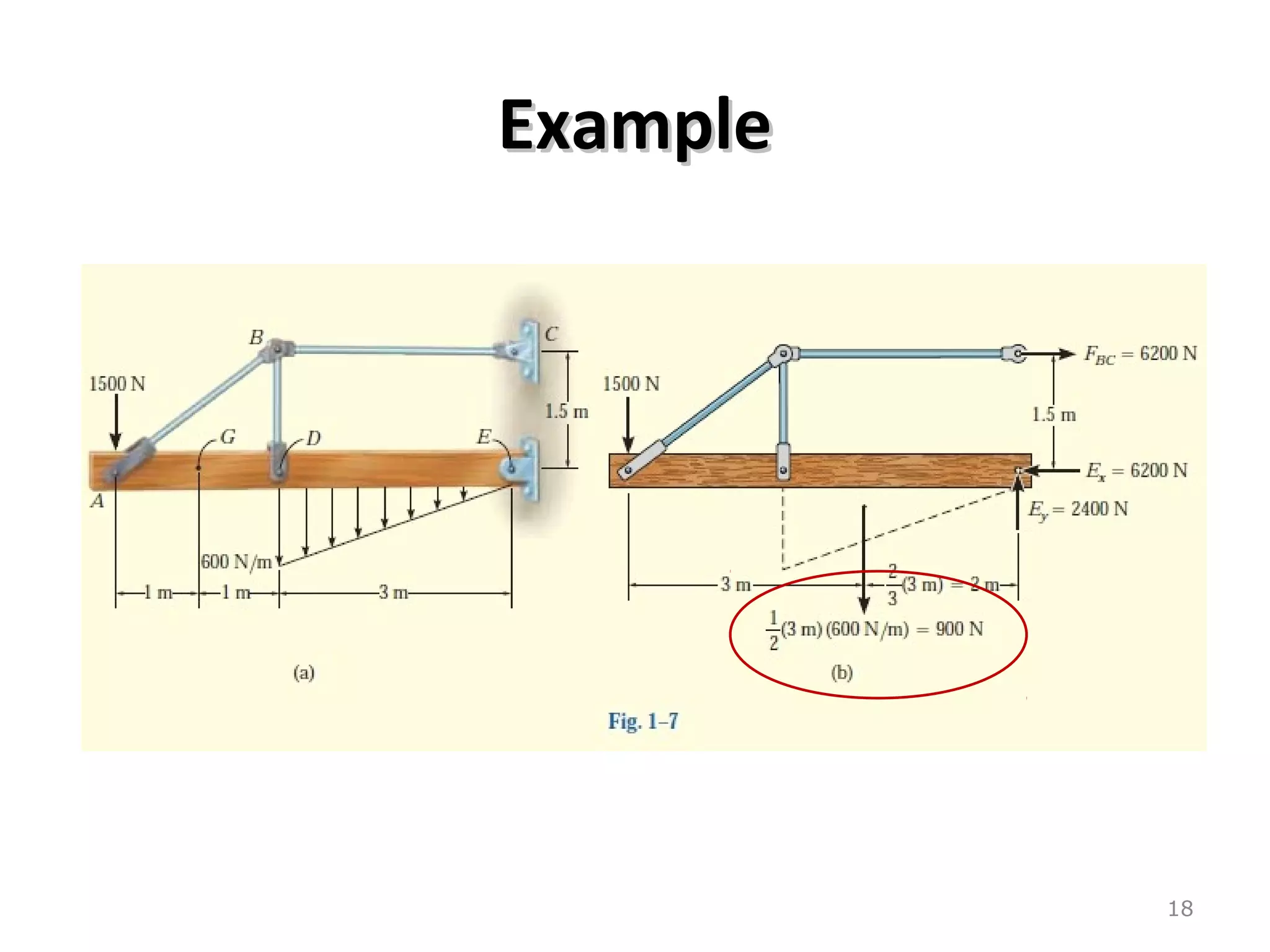
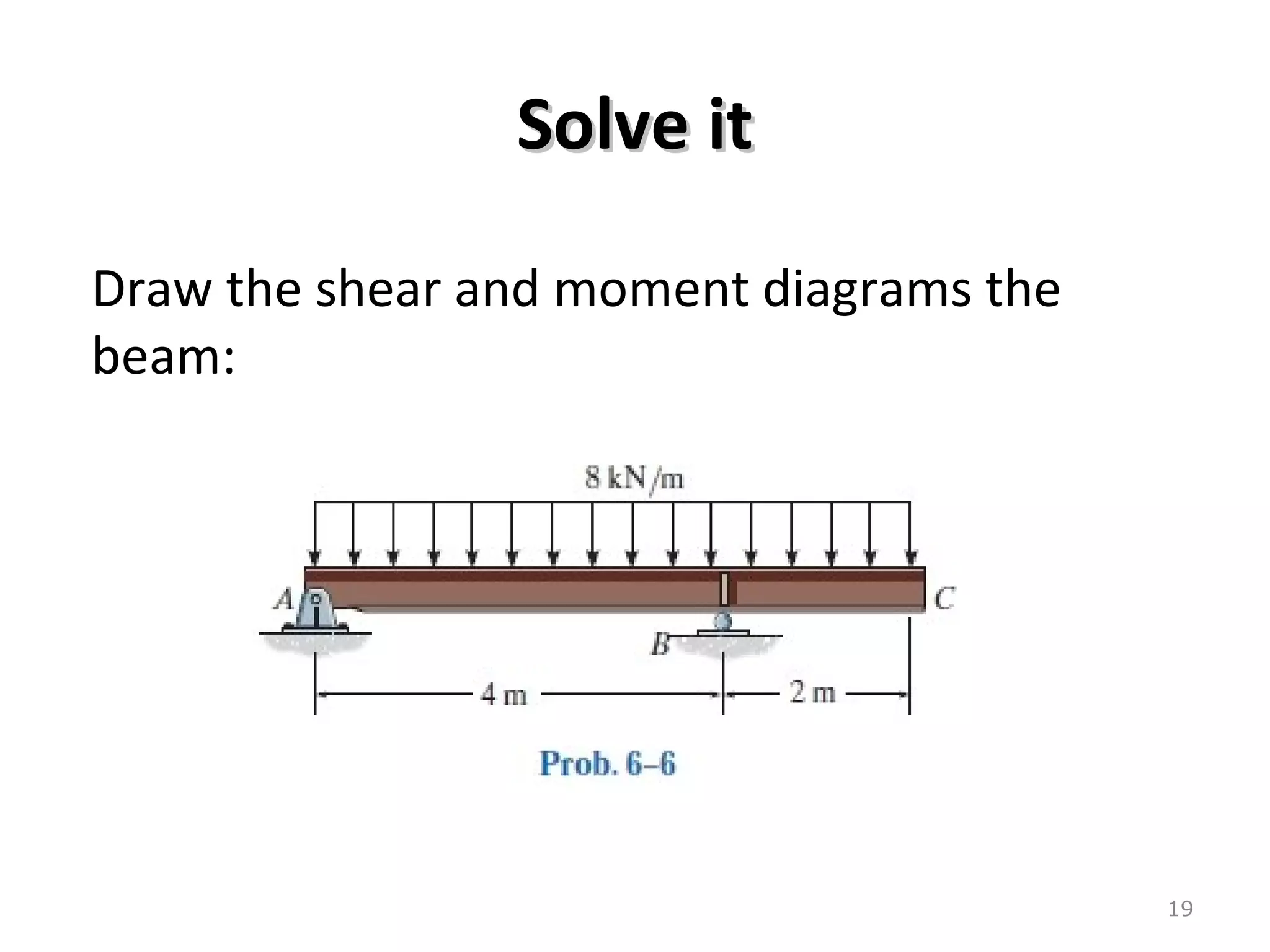
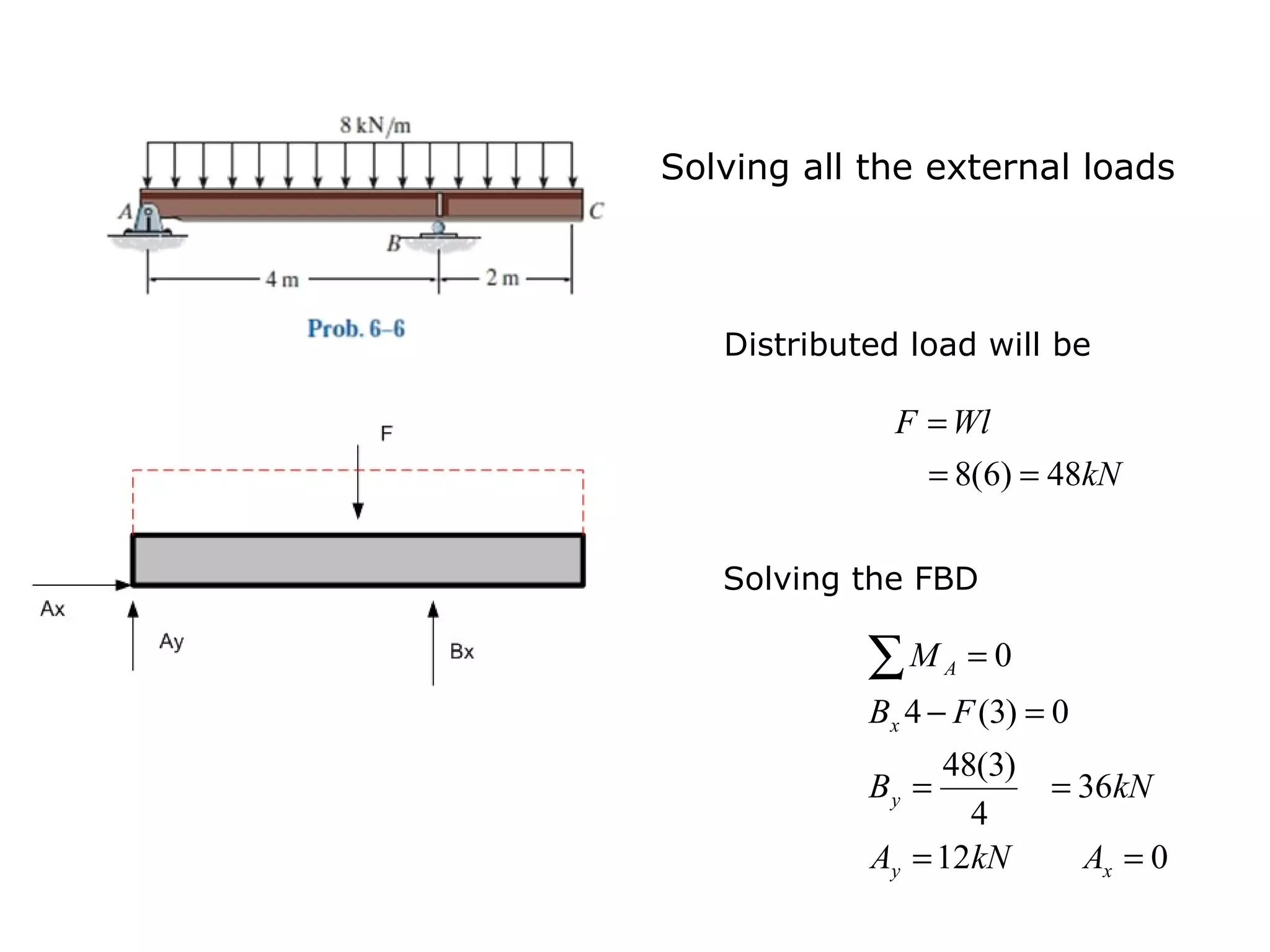
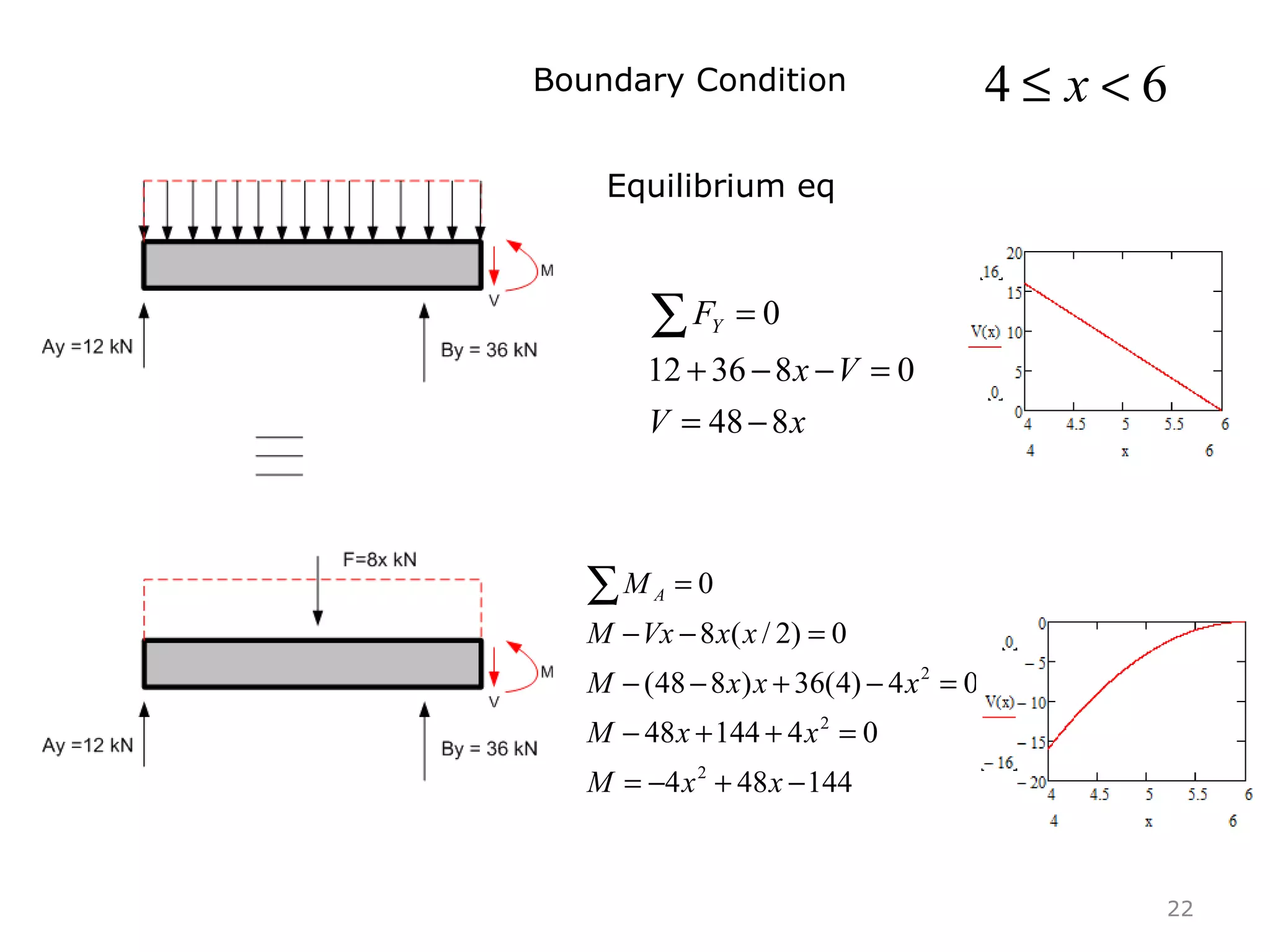
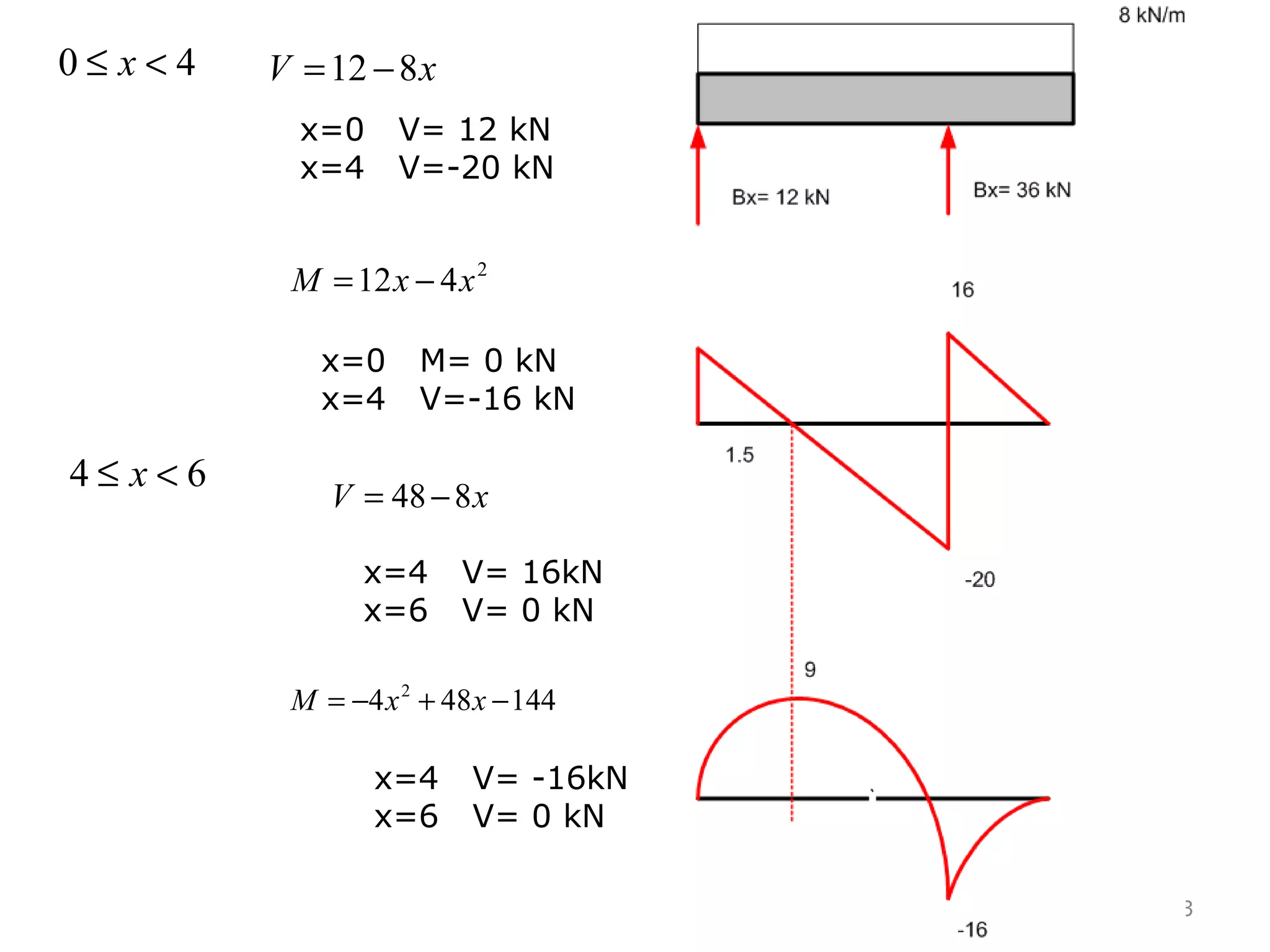
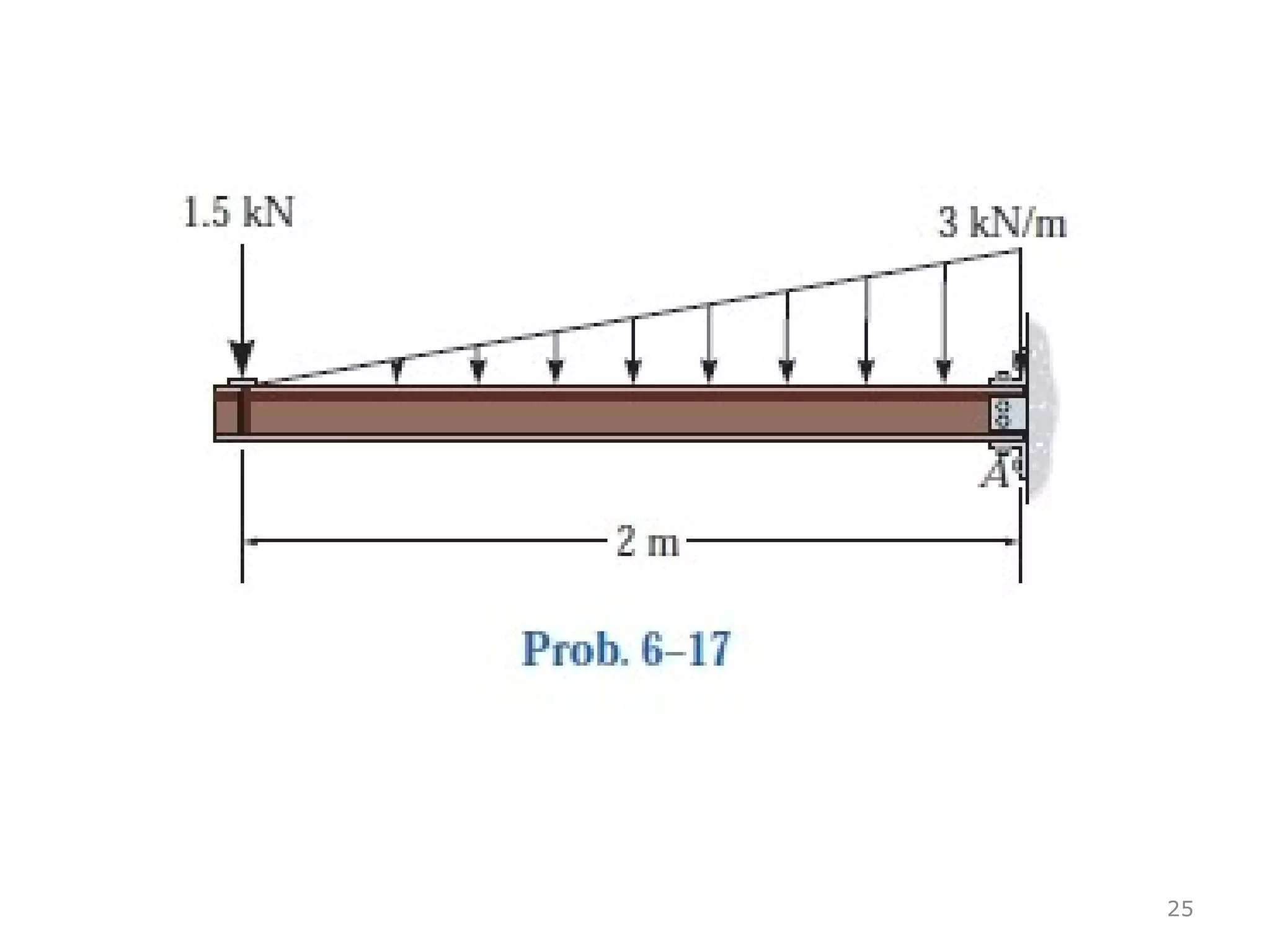
1) The document discusses shear and moment diagrams which graphically show the internal shear and moment forces acting on structural members. 2) It also discusses types of beams including simply supported, continuous, and cantilever beams. 3) Examples are provided for constructing shear and moment diagrams by taking the sum of moments and forces equal to zero and drawing the resulting diagrams based on the boundary conditions.

1. BendingBending
Shear and Moment Diagram,
Graphical method to construct shear
and moment diagram, Bending deformation of a
straight member, The flexure formula
1

2. 2

3. Shear and moment diagramShear and moment diagram
3
Axial load diagram
Torque diagram
Both of these diagrams show the internal forces acting on the members.
Similarly, the shear and moment diagrams show the internal shear and moment
acting on the members

4. Type of BeamsType of Beams
Statically Determinate
4
Simply Supported Beam
Overhanging Beam
Cantilever Beam

5. Type of BeamsType of Beams
Statically Indeterminate
5
Continuous Beam
Propped Cantilever Beam
Fixed Beam

6. 6

7. Example 1Example 1
Equilibrium equation for 0 ≤ x ≤ 3m:
A B
* internal V and M should be assumed +ve
kNV
VF
F y
9
0
0
−=
=−−
=∑
)(9
0
0
kNmxM
MVx
M
−=
=+
=∑
M
VF
x

8. Shear DiagramShear Diagram
Lecture 1 8
Sign convention: V= -9kN
M
VF
x

9. Shear DiagramShear Diagram
9
Sign convention: M= -9x kNm
X=0: M= 0
X=3: M=-27kNm
M=-9x
M = -9x kN.m
V = -9 kN
F
x

10. 10
V=9kN
M=X
At cross section A-A
X
At section A-A

11. Example 2Example 2
11
kN5
01050F
kN5
0)2()1(10;0
y
=
=−+=Σ
=
=−=Σ
y
y
y
yA
A
A
C
CM
1) Find all the external forces

12. 12
)(5
0
0
10
downkNV
VF
F
mx
y
=
=−
=
<≤
∑
)(5
0
0
10
ccwkNmVxM
VxM
M
mx
A
==
=−
=
<≤
∑
)(5
010
0
21
upkNV
VF
F
mx
y
=
=+−
=
≤≤
∑
)()510(
10
0)1(10
0
21
ccwkNmxM
VxM
MVx
M
mx
A
−=
−=
=+−
=
≤≤
∑
Force equilibrium
Force equilibrium
Moment equilibrium
Moment equilibrium

13. )(5
)(5
10
ccwxM
downkNV
mx
=
=
<≤
)(510
)(5
21
ccwxM
upkNV
mx
−=
=
<≤
M=5x
M=10-5x
Boundary cond for V and M

14. Solve itSolve it
Draw the shear and moment diagrams for
simply supported beam.
14

15. 15

16. Distributed LoadDistributed Load
16
For calculation purposes, distributed load can be represented as a single load
acting on the center point of the distributed area.
Total force = area of distributed load (W : height and L: length)
Point of action: center point of the area

17. ExampleExample
17

18. ExampleExample
18

19. Solve itSolve it
Draw the shear and moment diagrams the
beam:
19

20. Solving all the external loads
kN
WlF
48)6(8 ==
=
Distributed load will be
Solving the FBD
012
36
4
)3(48
0)3(4
0
==
==
=−
=∑
xy
y
x
A
AkNA
kNB
FB
M

21. 21
Boundary Condition 40 <≤ x
xV
Vx
FY
812
0812
0
−=
=−−
=∑
2
2
2
412
0412
04)812(
04
0
xxM
xxM
xxxM
xVxM
M A
−=
=+−
=−−−
=−−
=∑
Equilibrium eq

22. 22
Boundary Condition 64 <≤ x
xV
Vx
FY
848
083612
0
−=
=−−+
=∑
144484
0414448
04)4(36)848(
0)2/(8
0
2
2
2
−+−=
=++−
=−+−−
=−−
=∑
xxM
xxM
xxxM
xxVxM
M A
Equilibrium eq

23. 23
40 <≤ x
x=0 V= 12 kN
x=4 V=-20 kN
xV 812 −=
2
412 xxM −=
x=0 M= 0 kN
x=4 V=-16 kN
64 <≤ x
xV 848−=
x=4 V= 16kN
x=6 V= 0 kN
144484 2
−+−= xxM
x=4 V= -16kN
x=6 V= 0 kN

24. Graph based on equationsGraph based on equations
24
y = c Straight horizontal line
y = mx + c
y=3x + 3 y=-3x + 3
y=3x2
+ 3
y=-3x2
+ 3
y = ax2
+ bx +c

25. 25

26. Graphical methodGraphical method
26
( )
( ) xxwV
VVxxwV
Fy
∆−=∆
=∆+−∆−
=Σ↑+
0)(
:0
• Relationship between load and
shear:
( ) ( )[ ] ( )
( ) ( )2
0
:0
xkxwxVM
MMxkxxwMxV
Mo
∆−∆=∆
=∆++∆∆+−∆−
=Σ
• Relationship between shear and
bending moment:
26

27. 27
27
Dividing by ∆x and taking the limit as ∆x0, the
above two equations become:
Regions of distributed load:
Slope of shear
diagram at
each point
Slope of
moment
diagram
at each
point
= − distributed
load intensity
at each point
= shear at
each point
)(xw
dx
dV
−= V
dx
dM
=

28. ExampleExample
28

29. 29

30. 30
∫=∆ dxxwV )( ∫=∆ dxxVM )(
The previous equations become:
change in
shear =
Area under
distributed load
change in
moment =
Area under shear
diagram

31. 31
+ve area under shear diagram

32. 32

33. 33

34. Bending deformation of a straightBending deformation of a straight
membermember
34
Observation:
- bottom line : longer
- top line: shorter
- Middle line: remain the same but rotate (neutral line)

35. 35
Strain
s
ss
s ∆
∆−∆
=
>−∆
'
lim
0
ε
Before deformation
xs ∆=∆
After deformation, ∆x has a radius of
curvature ρ, with center of curvature at
point O’
θρ∆=∆=∆ xs
Similarly θρ ∆−=∆ )(' ys
ρ
ε
θρ
θρθρ
ε
y
y
s
−=
∆
∆−∆−
=
>−∆
)(
lim
0
Therefore

36. 36
ρ
ε
c
−=maxMaximum strain will be
max
max
)(
)
/
/
(
εε
ρ
ρ
ε
ε
c
y
c
y
−=
−=
max)( σσ
c
y
−=
-ve: compressive state
+ve: tension

37. The Flexure FormulaThe Flexure Formula
37
The location of neutral axis is
when the resultant force of the
tension and compression is equal
to zero.
∑ == 0FFR
Noting
dAdF σ=
∫
∫
∫∫
−=
−=
==
A
A
A
ydA
c
dA
c
y
dAdF
max
max)(
0
σ
σ
σ

38. 38
Since , therefore
Therefore, the neutral axis should
be the centroidal axis
0max
≠
c
σ 0=∫A
ydA

39. 39
∑= ZZR MM )(
∫
∫
∫ ∫
=
=
==
A
A
A A
dAy
c
dA
c
y
y
dAyydFM
2max
max)(
σ
σ
σ
I
Mc
=maxσ
Maximum normal stress
Normal stress at y distance
I
My
=σ

40. Line NA: neutral axis
Red Line: max normal stress
c = 60 mm
Yellow Line: max compressive stress
c = 60mm
I
Mc
=maxσ
I
Mc
−=maxσ
Line NA: neutral axis
Red Line: Compressive stress
y1 = 30 mm
Yellow Line: Normal stress
y2 = 50mm
I
My1
1 −=σ
I
My2
2 =σ
Refer to Example 6.11 pp 289

41. I: moment of inertial of the crossI: moment of inertial of the cross
sectional areasectional area
12
3
bh
I xx =−
644
44
Dr
I xx
ππ
==−
Find the stresses at
A and B

42. I: moment of inertial of the crossI: moment of inertial of the cross
sectional areasectional area
Locate the centroid (coincide
with neutral axis)
mm
AA
AyAy
A
Ay
y n
i
i
n
i
ii
5.237
)300)(50()300)(50(
)300)(50(325)300)(50(150
21
2211
1
1
=
+
+
=
+
+
=
=
∑
∑
=
=

43. I: moment of inertial of the crossI: moment of inertial of the cross
sectional areasectional area
Profile I
46
33
)10(5.112
12
)300(50
12
mm
bh
II ===
A A
46
262
3
)10(344.227
)5.87)(300)(50()10(5.112
12
)(
mm
Ad
bh
I AAI
=
+=+=−
I about Centroidal axis
I about Axis A-A using parallel axis
theorem
Profile II
46
2
3
2
3
)10(969.117
)5.87)(50)(300(
12
)50)(300(
12
)(
mm
Ad
bh
I AAII
=
+=+=−
Total I
46
466
)10(313.345
)10(969.117)10(344.227
)()(
mm
mm
III AAIIAAIAA
=
+=
+= −−−
* Example 6-12 to 6-14 (pp 290-292)

44. Solve itSolve it
If the moment acting on the cross section of the beam is M = 6 kNm,
determine the maximum bending stress on in the beam. Sketch a
three dimensional of the stress distribution acting over the cross
section
If M = 6 kNm, determine the resultant force the bending stress
produces on the top board A of the beam

45. 46
3
2
3
)10(8.786
12
)300(40
])170)(40)(300(
12
)40(300
[2
mm
II
=
++=
Total Moment of Inertia
Max Bending Stress at the top and bottom
MPa
II
Mc
Mtop 45.1
)190()10(6000 3
−=
−
=−=
MPaMbottom 45.1=
Bottom of the flange
MPa
II
Mc
M topf 14.1
)150()10(6000 3
_ −=
−
=−=
MPaM bottomf 14.1_ =
1.45MPa
1.14MPa
6kNm

46. Resultant F = volume of the trapezoid
1.45MPa
1.14MPa
40 mm
300 mm
kN
NFR
54.15
15540)300)(40(
2
)14.145.1(
=
=
+
=

47. Solve itSolve it
The shaft is supported by a smooth thrust load at A and smooth
journal bearing at D. If the shaft has the cross section shown,
determine the absolute maximum bending stress on the shaft

48. Draw the shear and moment diagram
kNF
kNF
F
M
A
D
D
A
3
3
)25.2(3)75.0(3)3(
0
=
=
+=
=∑
External Forces
Absolute Bending
Stress
Mmax = 2.25kNm
MPa
I
Mc
8.52
)2540(
4
)40()10(2250
44
3
max
=
−
==
π
σ