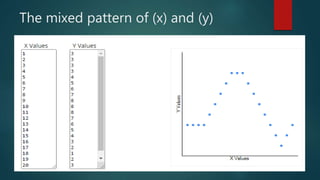
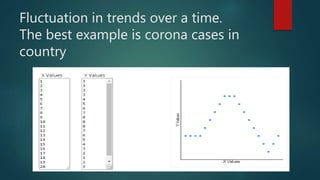
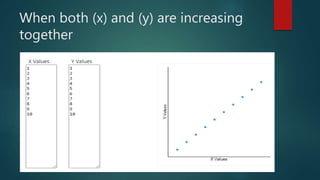
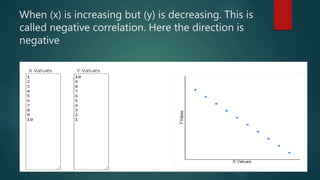
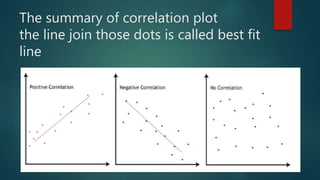
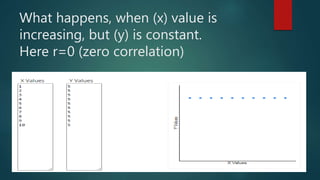
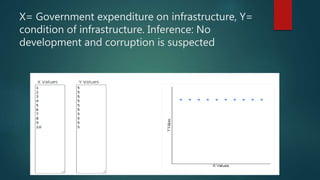
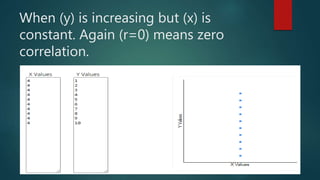
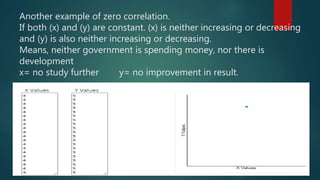
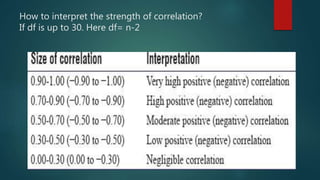
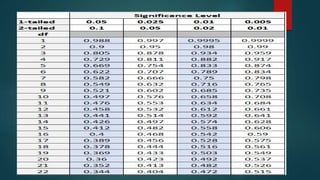
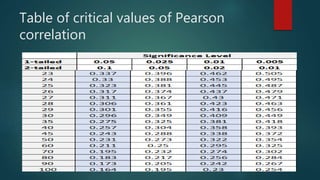
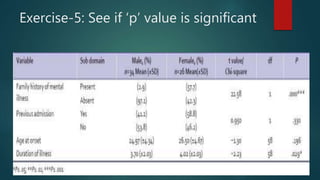
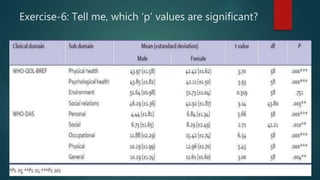
This document discusses the basic concepts of correlation including: 1. Correlation measures the strength and direction of association between two continuous variables. A positive correlation means both variables increase together, while a negative correlation means one increases as the other decreases. 2. The coefficient of correlation, r, indicates the strength of correlation, ranging from -1 to 1. Zero correlation means there is no linear relationship between the variables. 3. Correlation does not imply causation - it only shows association. Changes in one variable may not cause changes in the other. 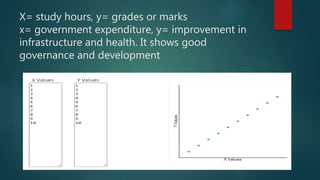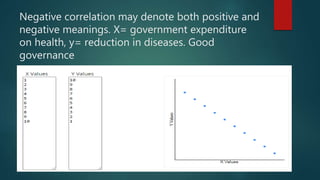4. Examples are provided to illustrate different correlation strengths and directions between variables like government spending/infrastructure development, police action/crime rates, and study

1. The Basic Understanding of
Correlation
DR. RAJEEV KUMAR, M.S.W. (TISS, MUMBAI), M.PHIL. (CIP,
RANCHI), UGC-JRF, PH.D. (IIT KHARAGPUR)

2. What is correlation?

3. The components of correlation
What is the meaning of ‘r’
‘r’ is the coefficient of correlation, it tells the strength or weakness of
correlation
Direction of correlation
The direction is denoted by sign of positive or negative.

4. Few things to remember in Pearson’s
Correlation
 It shows the association between two continuous variables.
 Correlation is always bidirectional
A B . It means, if A is increasing B is also increasing. In case of
positive correlation.
In case of negative correlation, A is increasing, B is decreasing.
But correlation does not show causative relation.
Means B is not increasing due to A.
A is not influencing B
A is not predicting B
It is a linear relation

5. What happens, when (x) value is
increasing, but (y) is constant.
Here r=0 (zero correlation)

6. X= Government expenditure on infrastructure, Y=
condition of infrastructure. Inference: No
development and corruption is suspected

7. When (y) is increasing but (x) is
constant. Again (r=0) means zero
correlation.

8. X= Police action Y= crime rate
police is taking some action and crime is increasing. It
means, there is failure of police. And many reasons may be
behind it. Corruption is one of them

9. Another example of zero correlation.
If both (x) and (y) are constant. (x) is neither increasing or decreasing
and (y) is also neither increasing or decreasing.
Means, neither government is spending money, nor there is
development
x= no study further y= no improvement in result.

10. When both (x) and (y) are increasing
together

11. X= study hours, y= grades or marks
x= government expenditure, y= improvement in
infrastructure and health. It shows good
governance and development

12. When (x) is increasing but (y) is decreasing. This is
called negative correlation. Here the direction is
negative

13. Negative correlation may denote both positive and
negative meanings. X= government expenditure
on health, y= reduction in diseases. Good
governance

14. The mixed pattern of (x) and (y)

15. Fluctuation in trends over a time.
The best example is corona cases in
country

16. The summary of correlation plot
the line join those dots is called best fit
line

17. How to calculate the correlation

18. How to interpret the strength of correlation?
If df is up to 30. Here df= n-2

20. Table of critical values of Pearson
correlation

22. Exercise -1: just check whether the correlation is significant
??
A study among 35 college students to see the correlation
between social support and GPA

23. Exercise-2: A study among 12 students to see the
correlation between motivation and success.
Whether correlation is signification?

24. Exercise-3: A study was conducted among 10 individual
to assess correlation between age and cholesterol. See if
the correlation is significant ?

25. Understanding p value
How to interpret the ‘p’ value
 If value of ‘p’ is less than or equal to
.05, then p is significant at 0.05. we
can say (p≤.05) and CI=95%
 If value of ‘p’ is less than or equal to
.01, then p is significant at 0.01. we
can say (p≤.01) and CI=99%
 If value of ‘p’ is less than or equal to
.001, then p is significant at 0.001. we
can say (p≤.001) and CI=99.99%
It means it tested at CI=99.99%
( p= 0.001)

26. Exercise- 4
find out the significant ‘p’ values and at what alpha
level
 .86 .76 .0007 .0008 .000001 .93 .0003
 .98 .06 .006 .63 .054 .049 .051
 .56
 .007
 .09
 .54
 .18
 .01

27. Exercise-5: See if ‘p’ value is significant

28. Exercise-6: Tell me, which ‘p’ values are significant?

29. Thanks!
Keep learning!
In the next session, we will learn how
to calculate the Pearson Correlation,
manually.