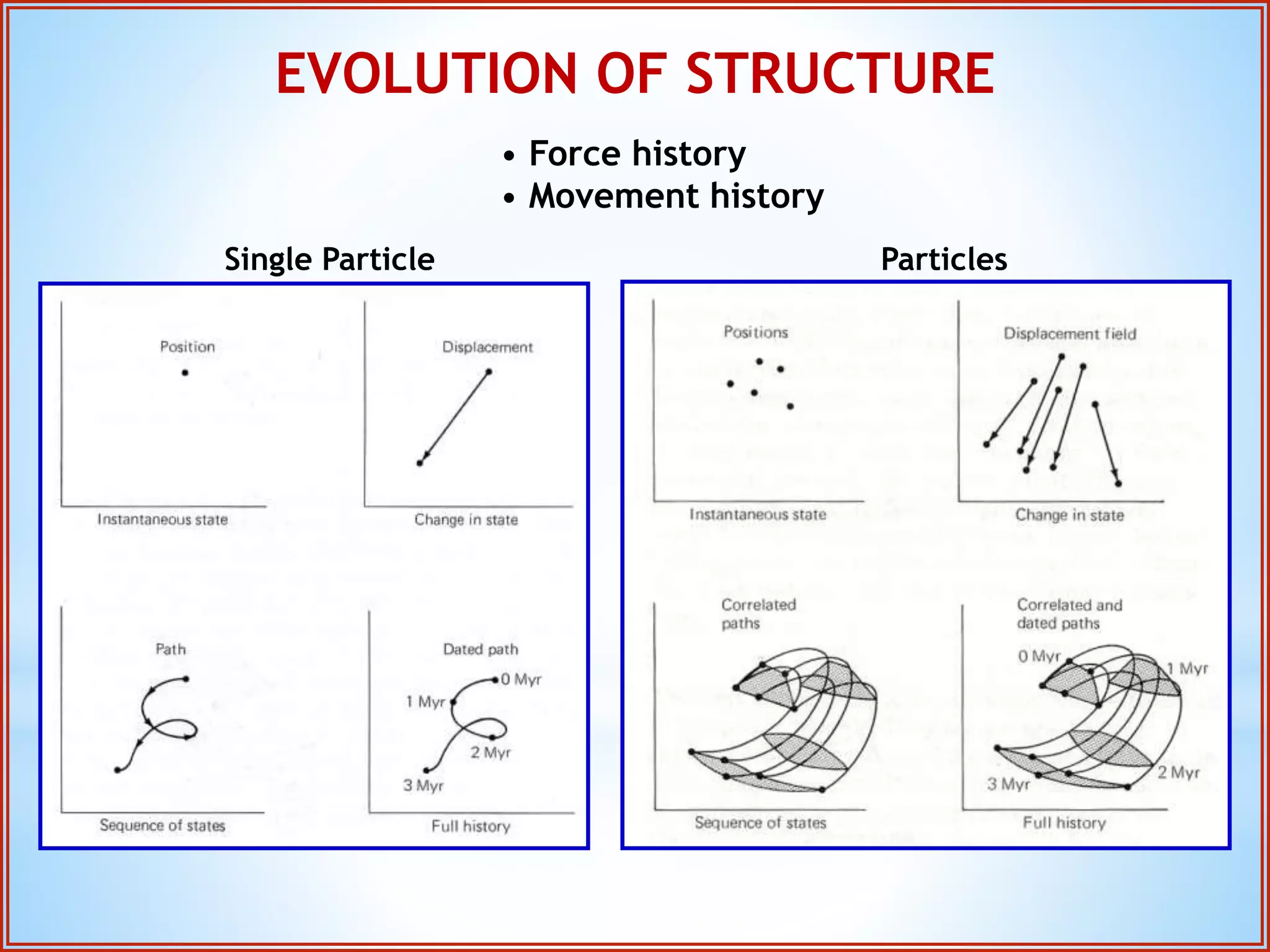
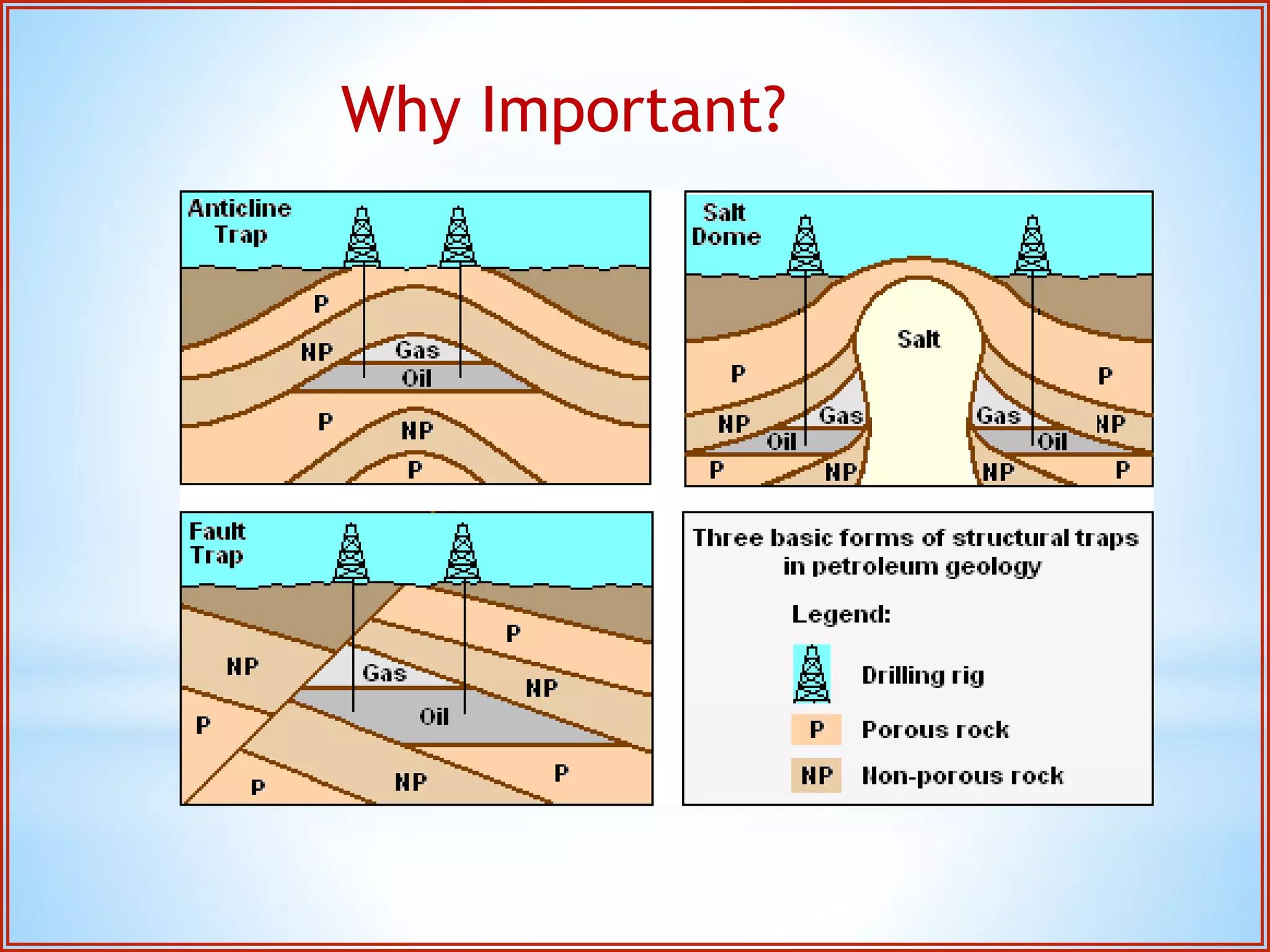
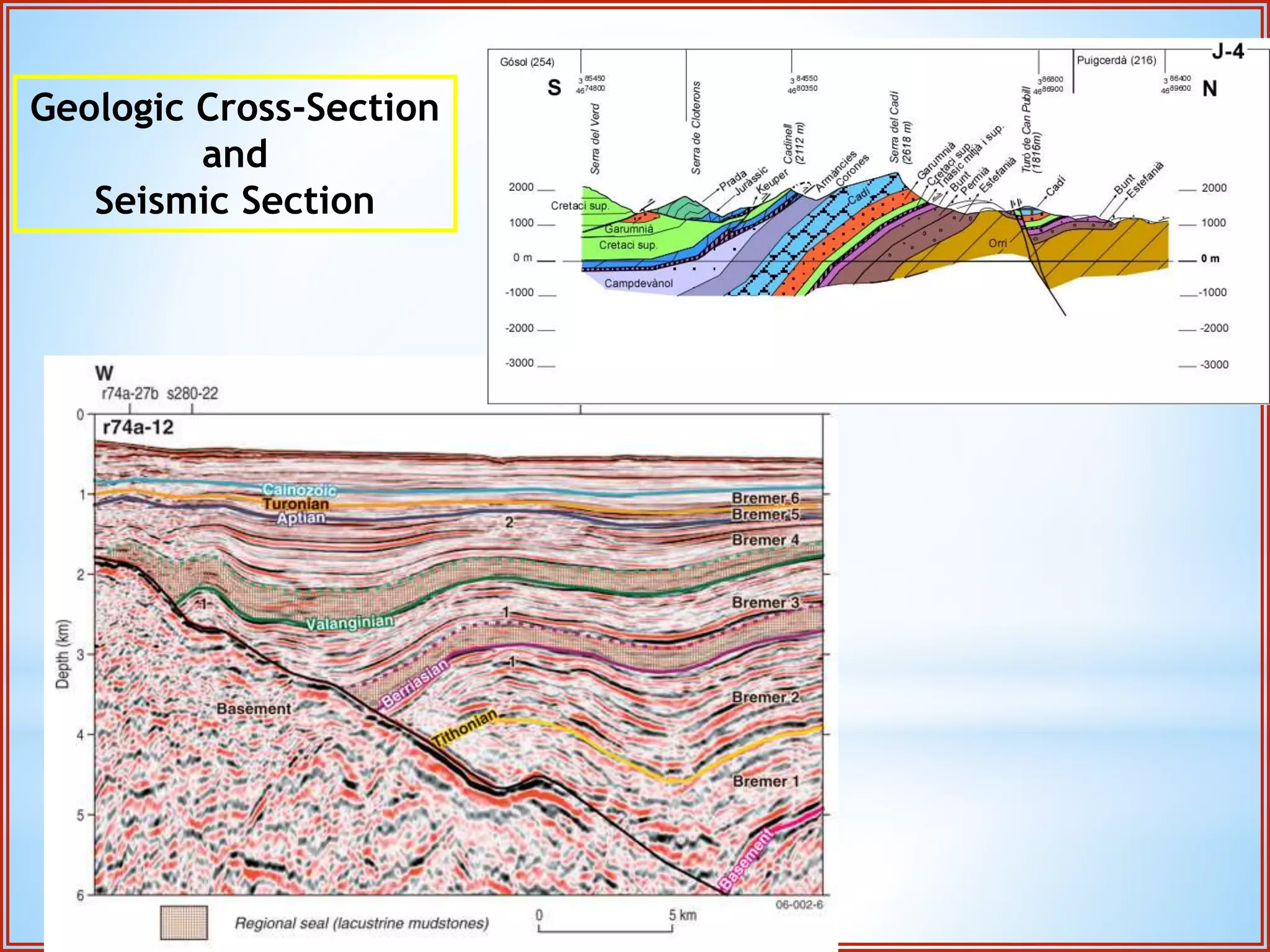
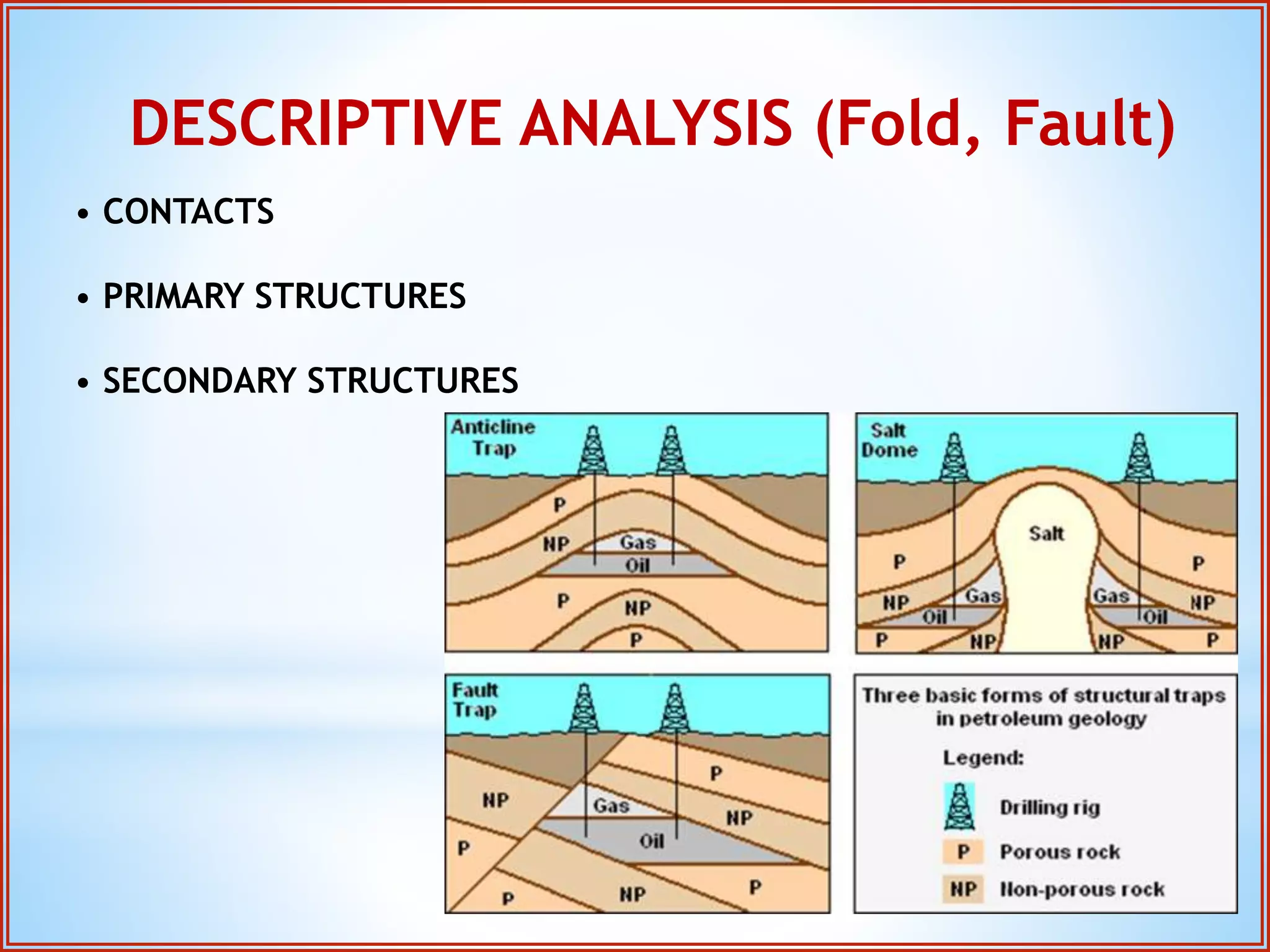
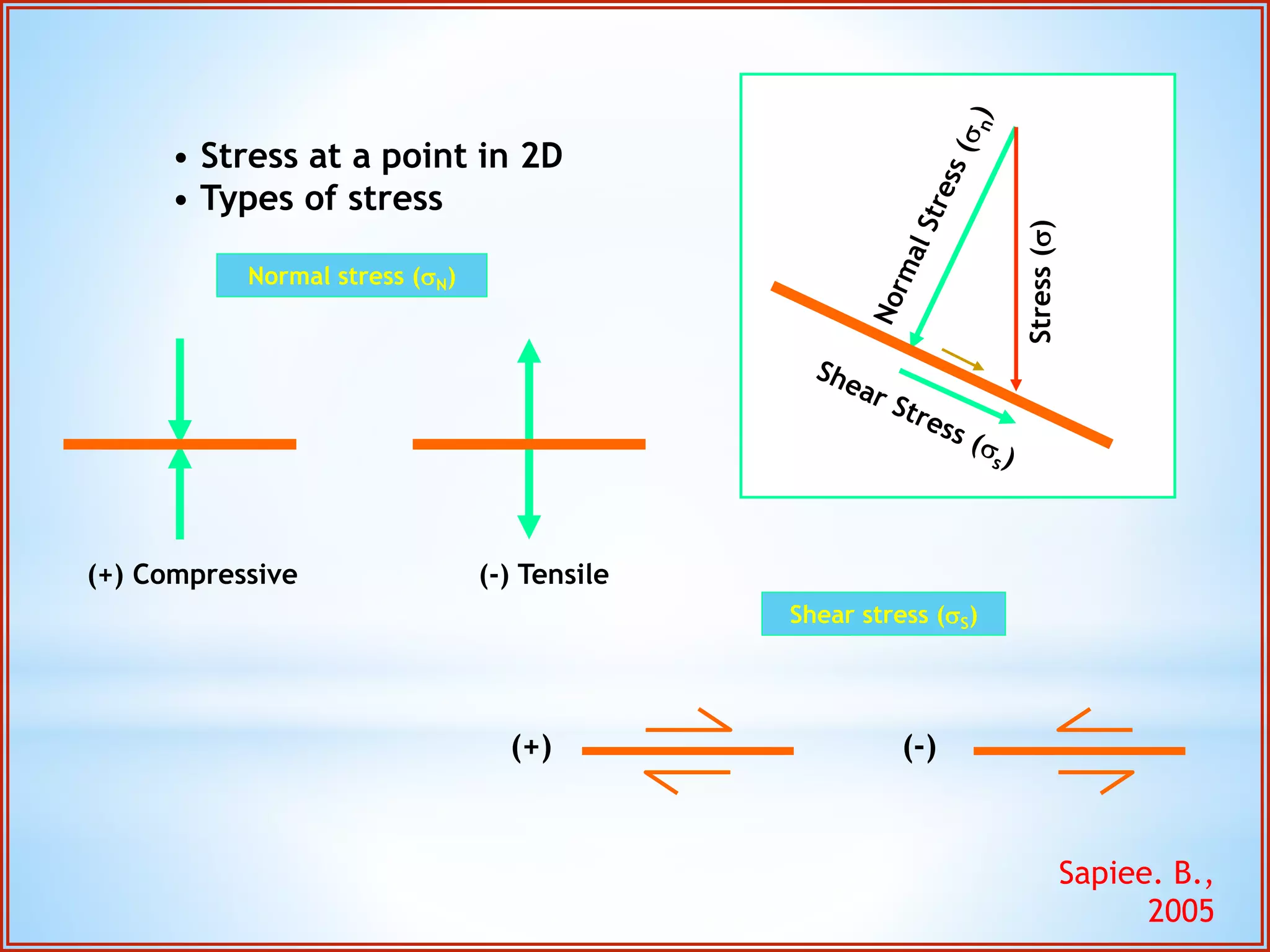
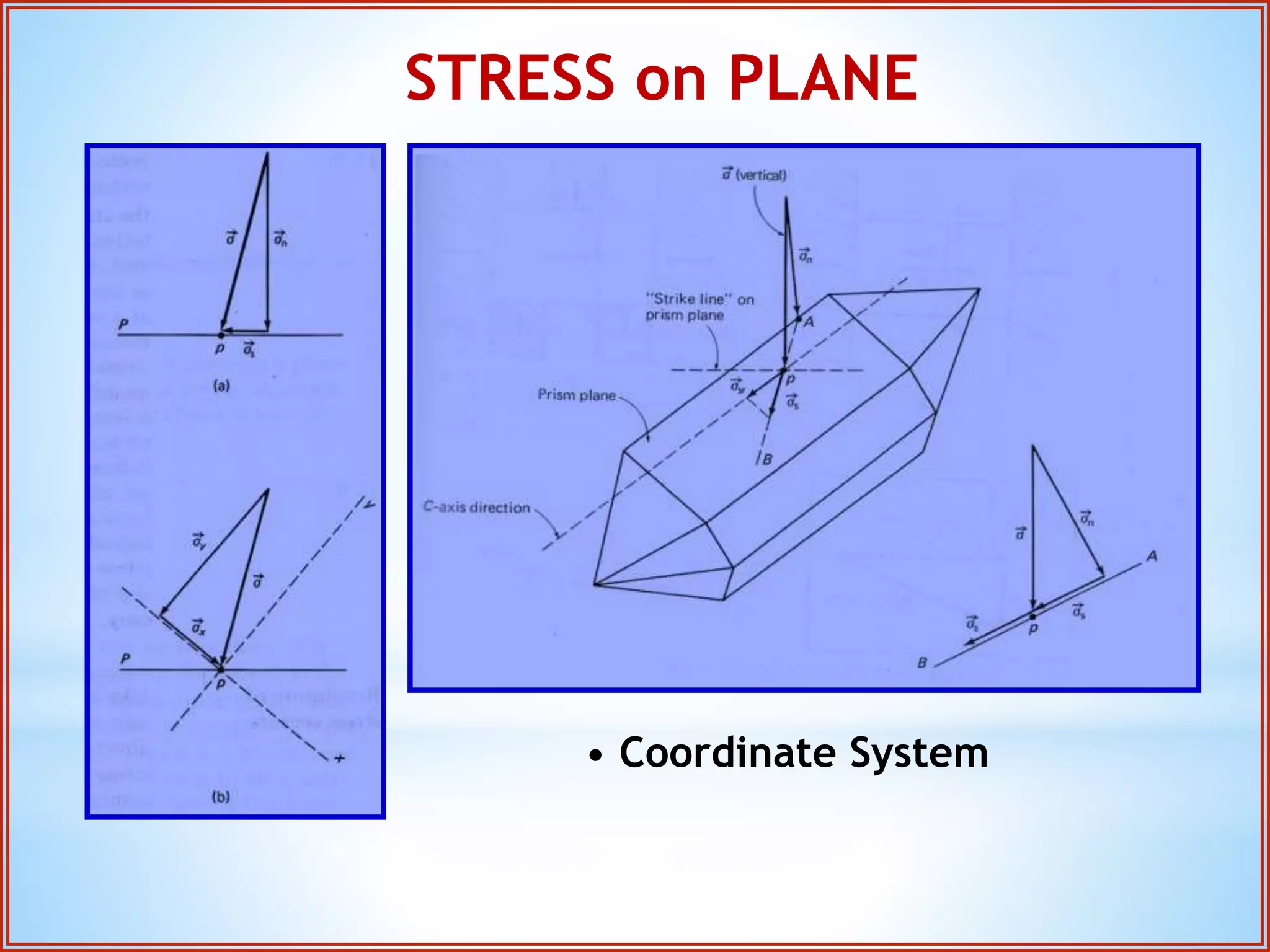
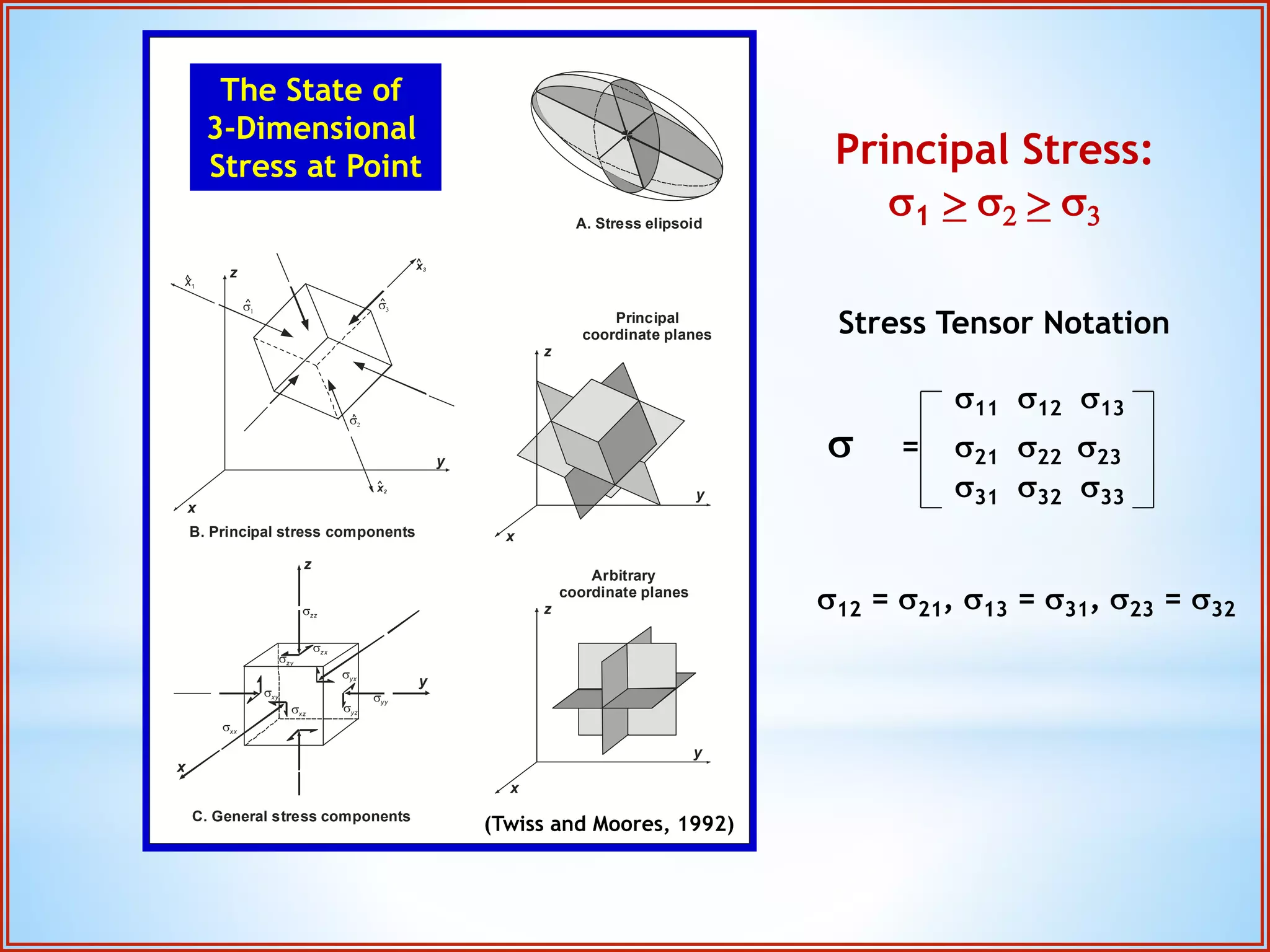
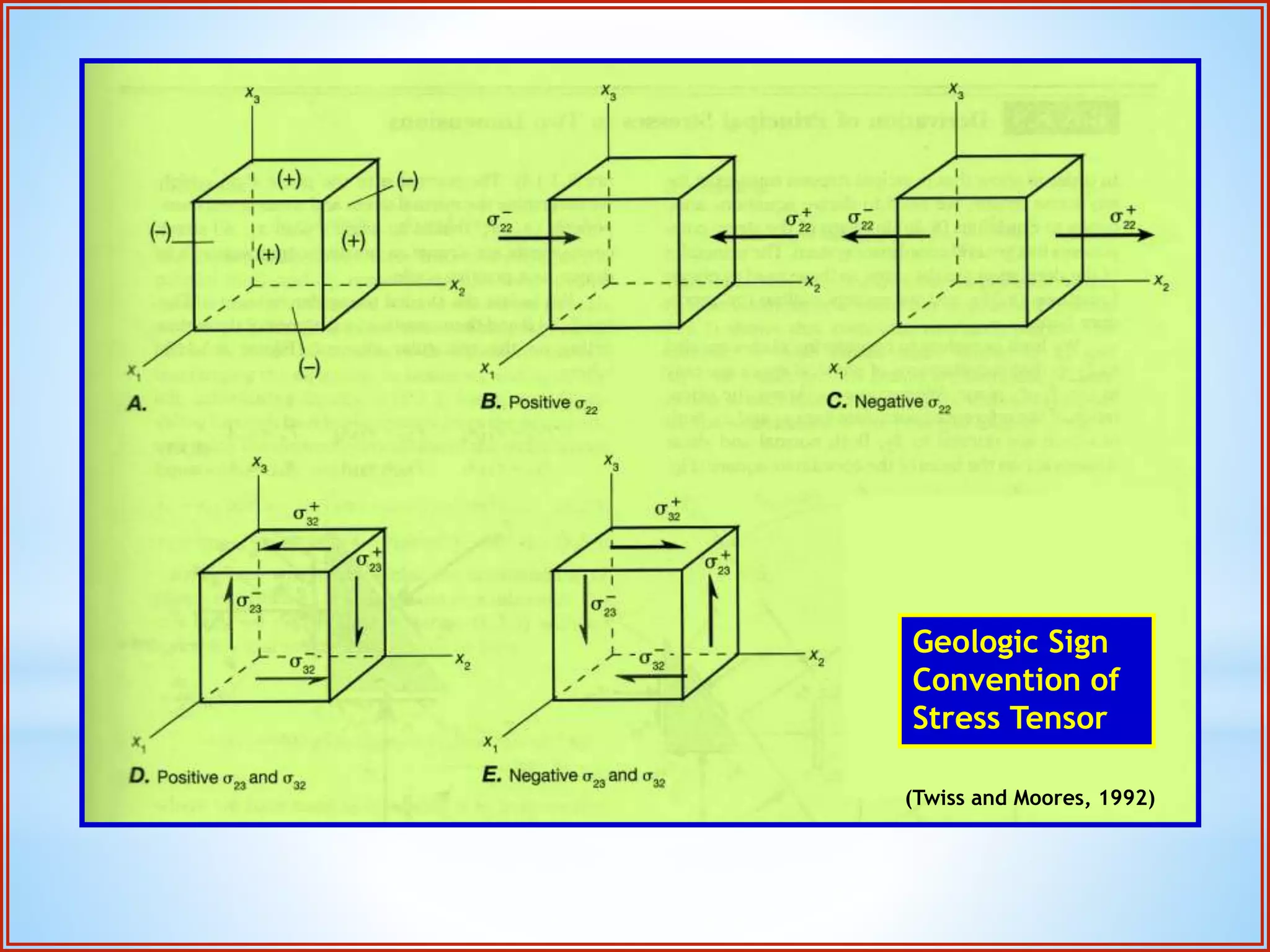
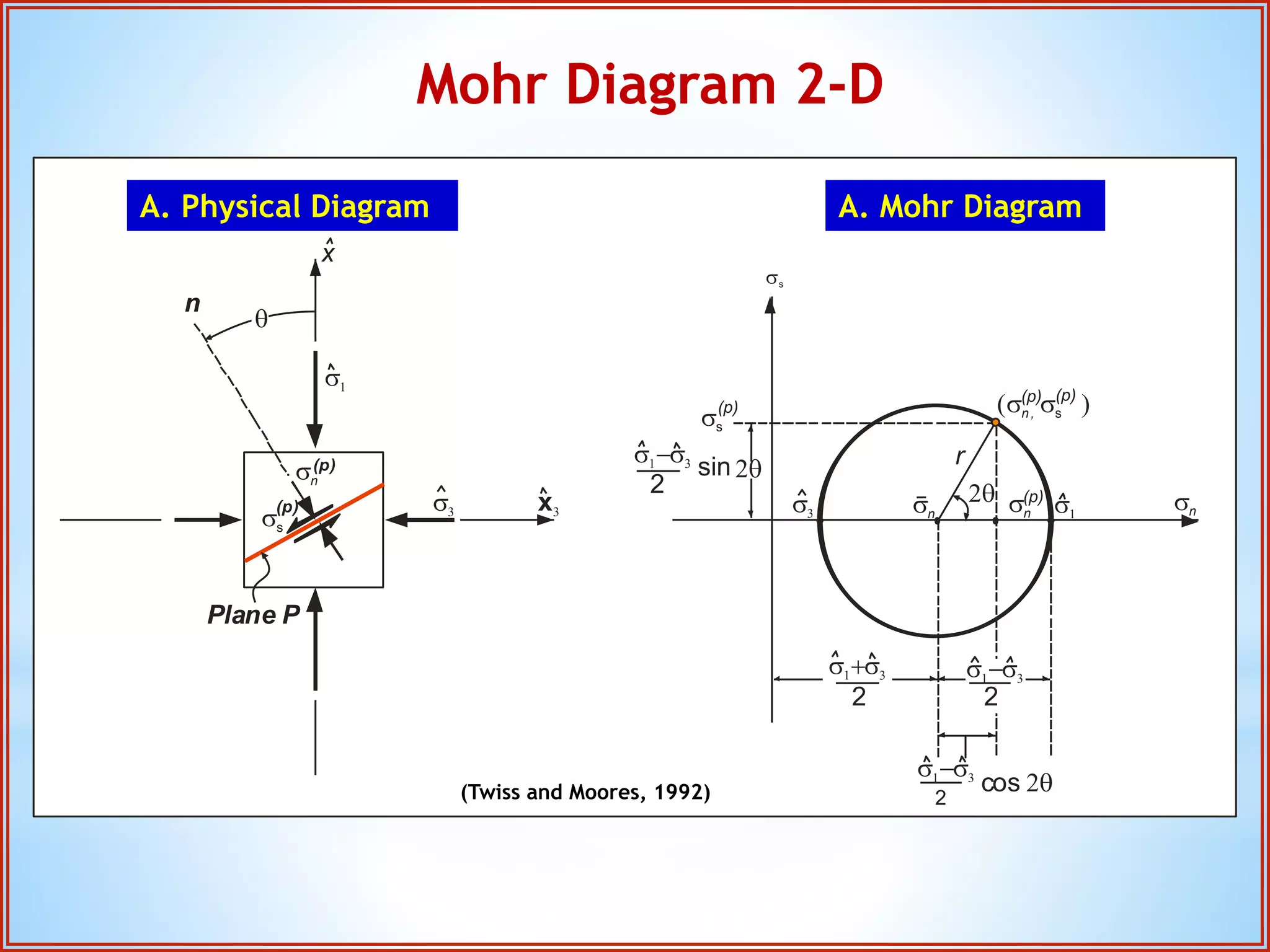
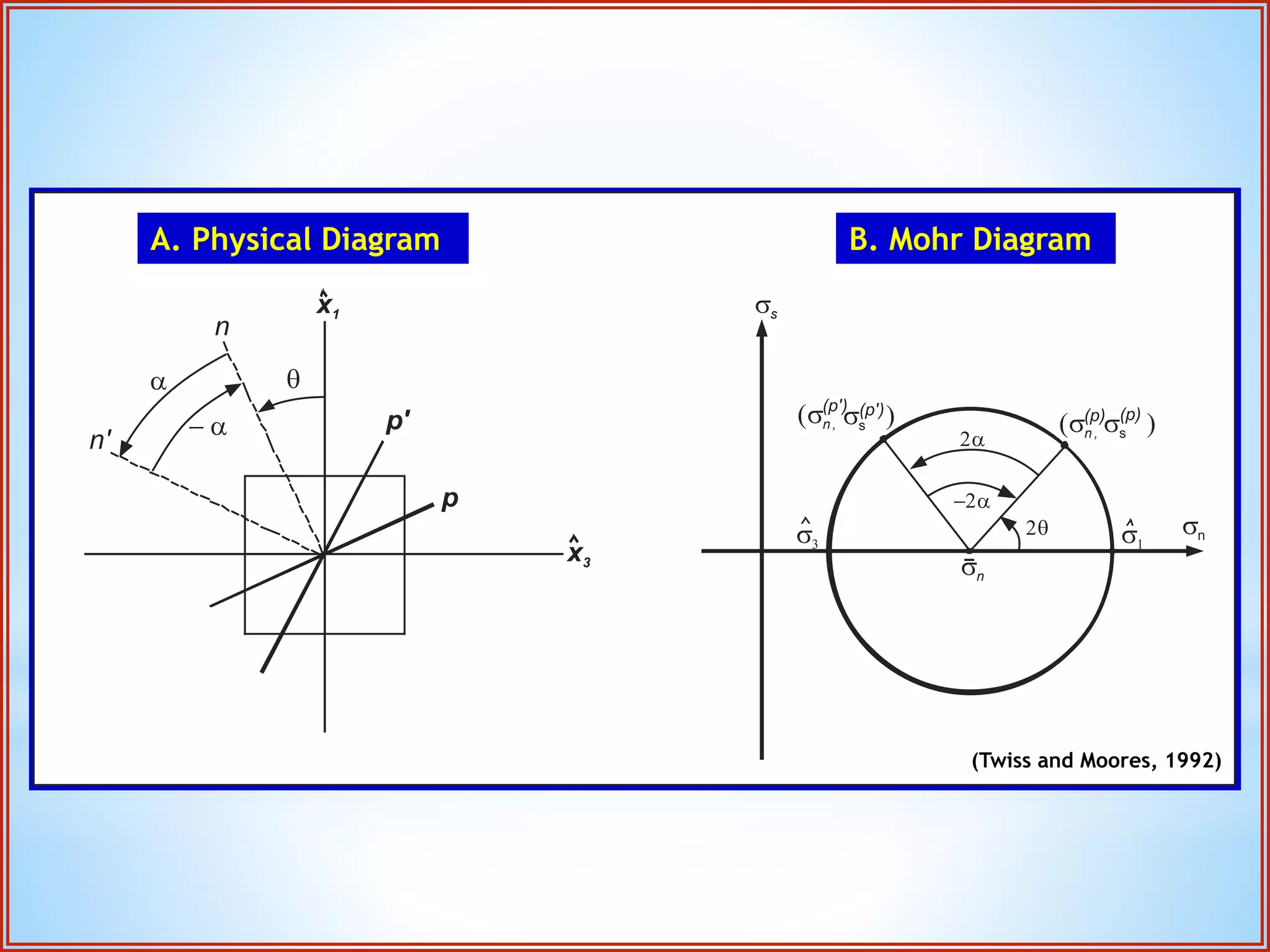
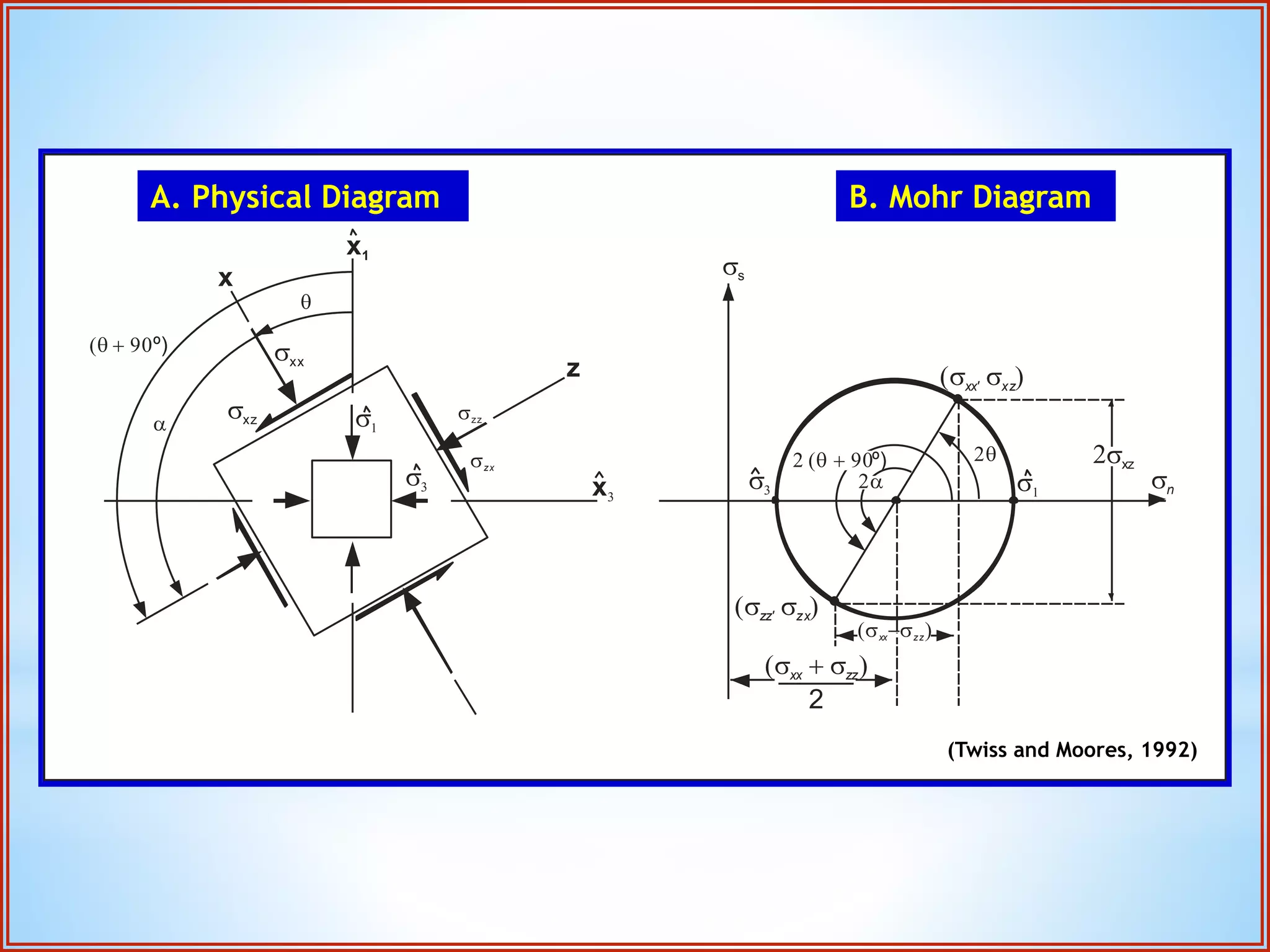
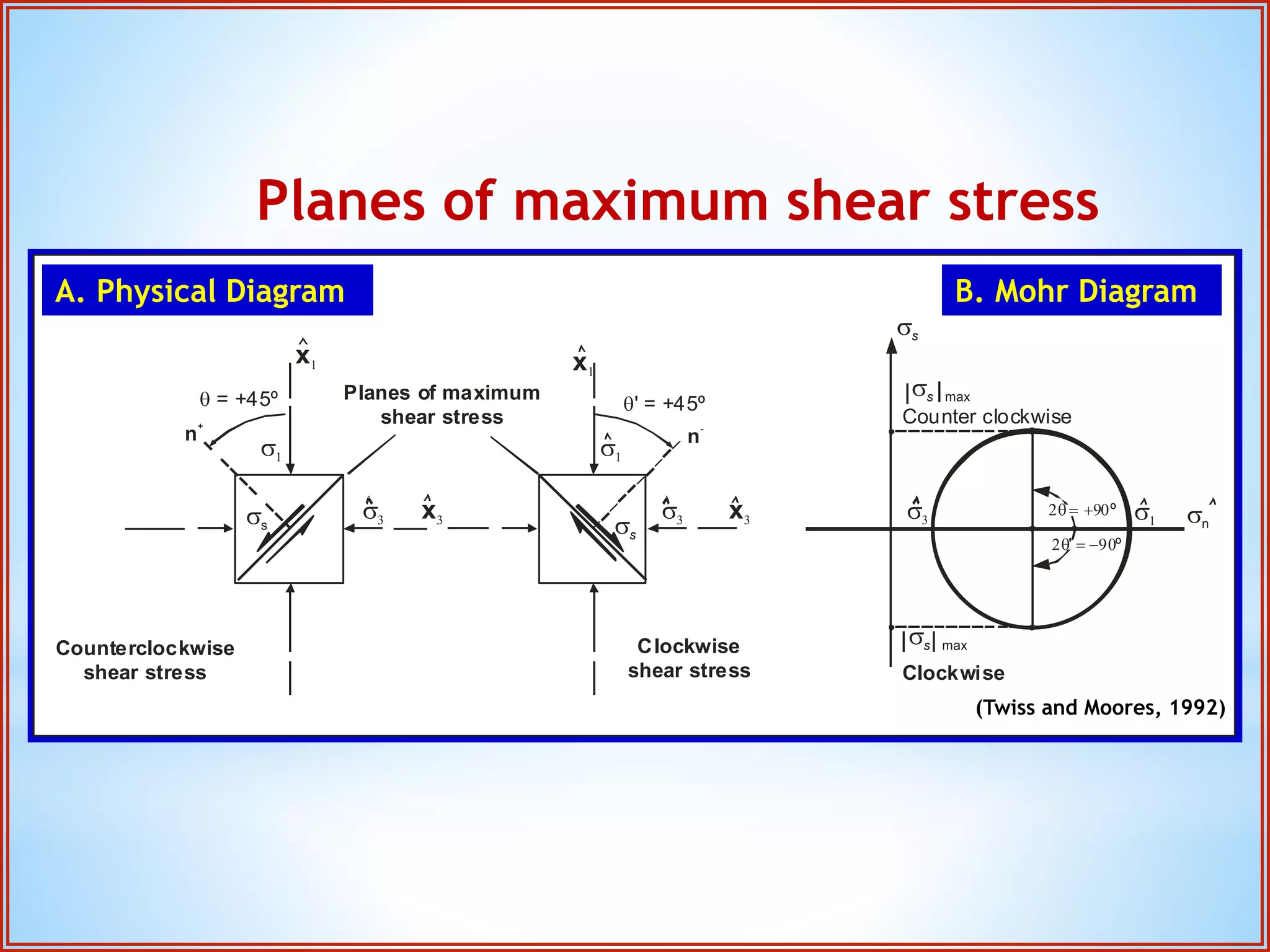
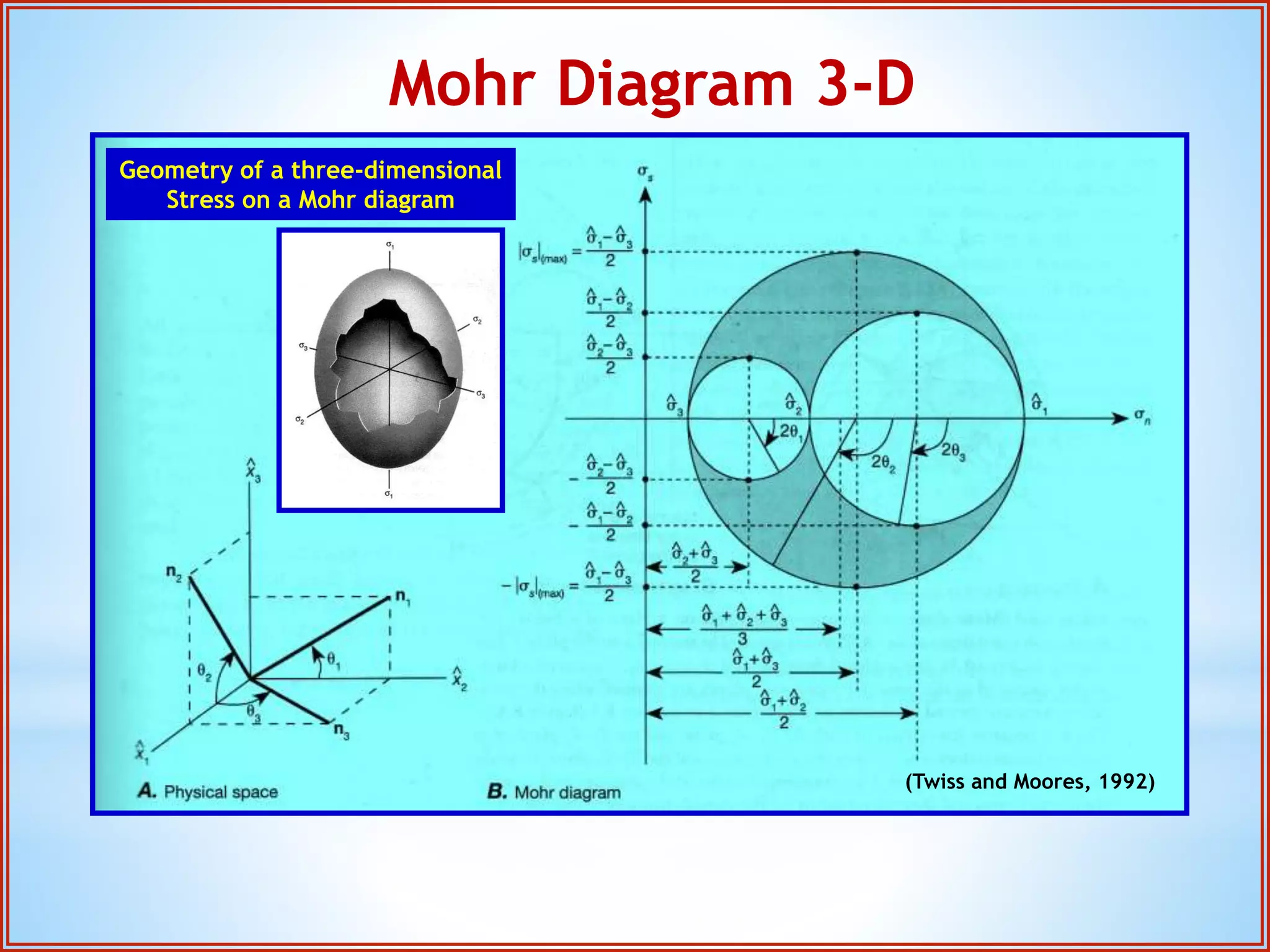
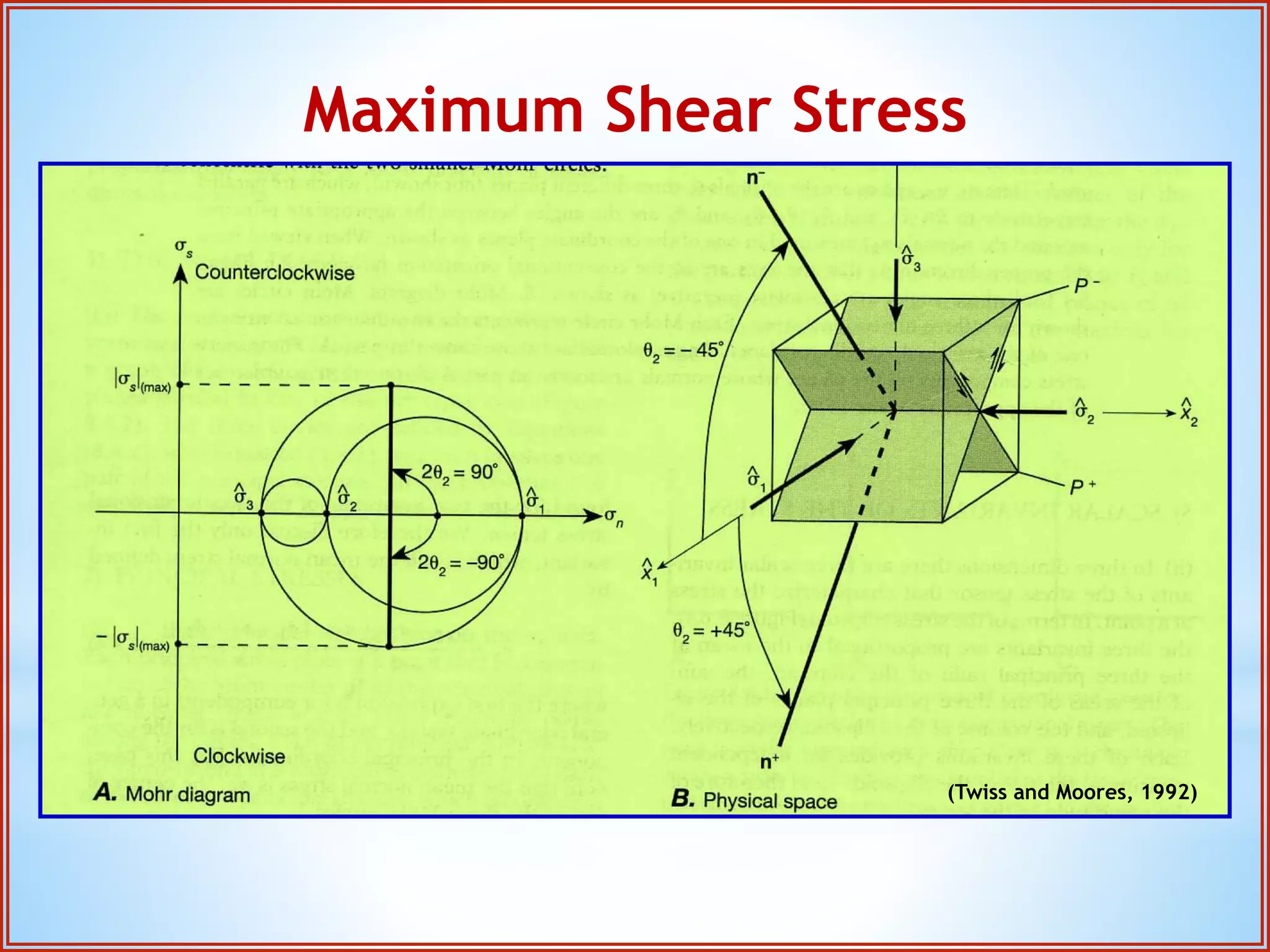
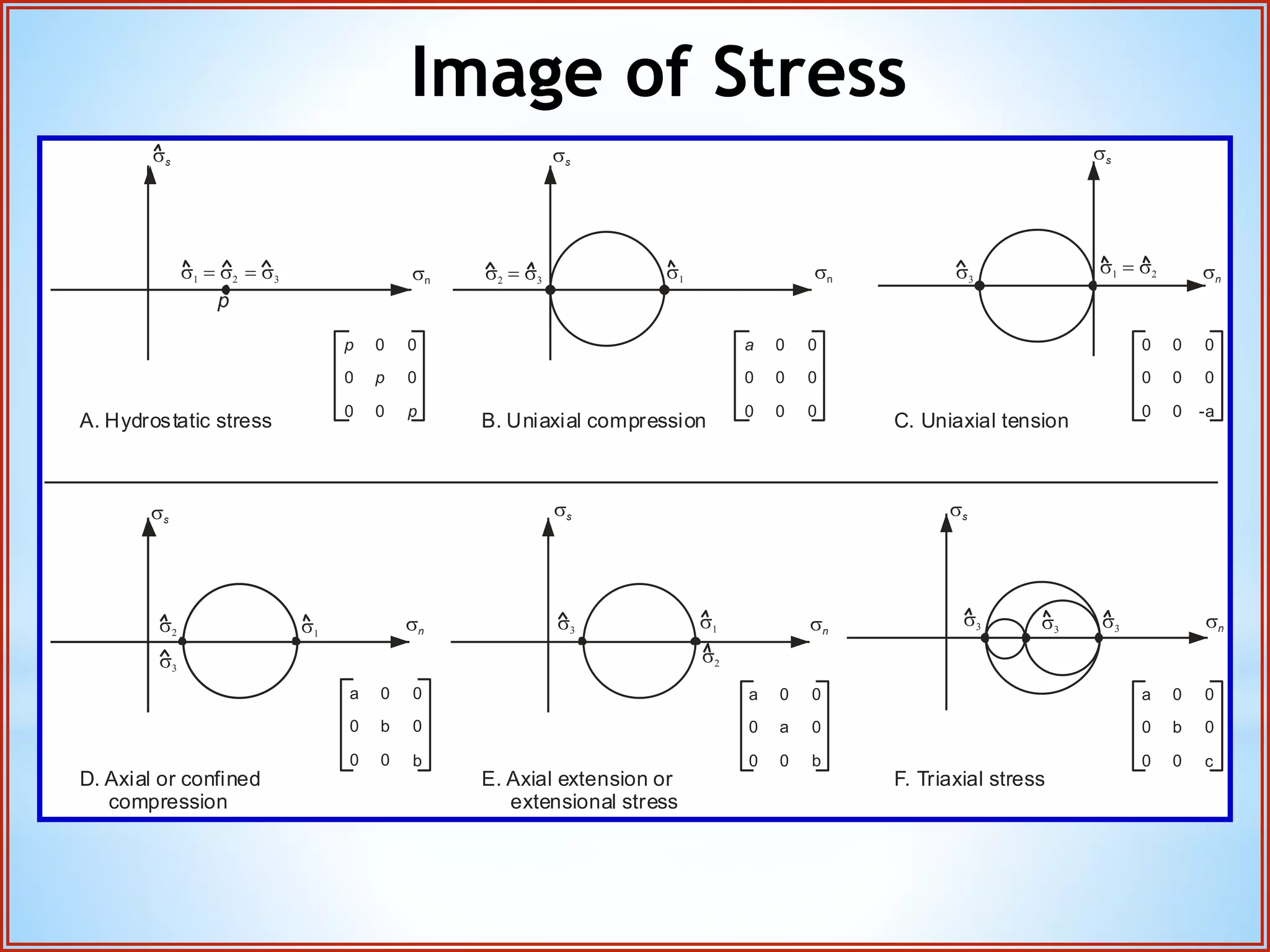
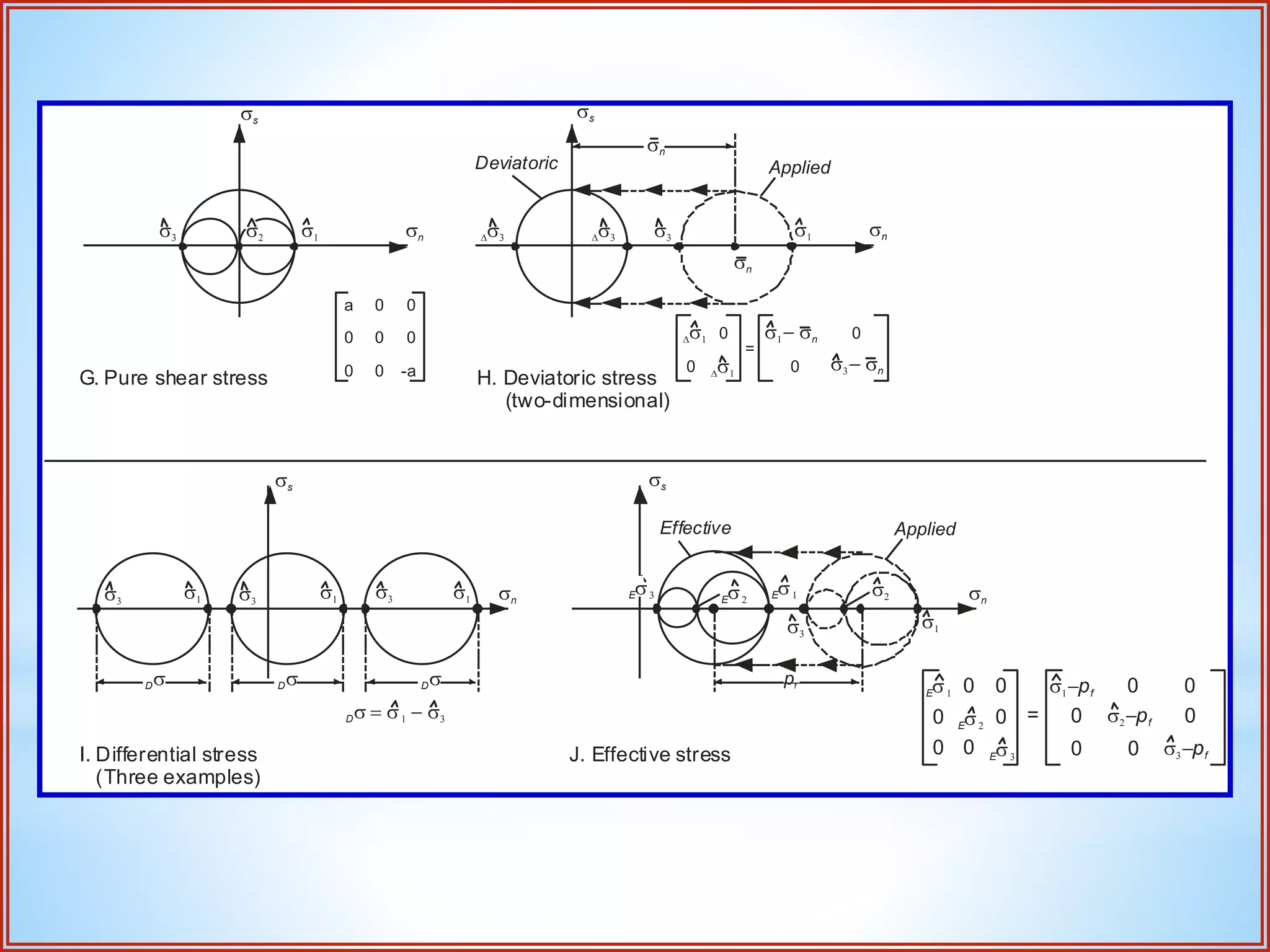
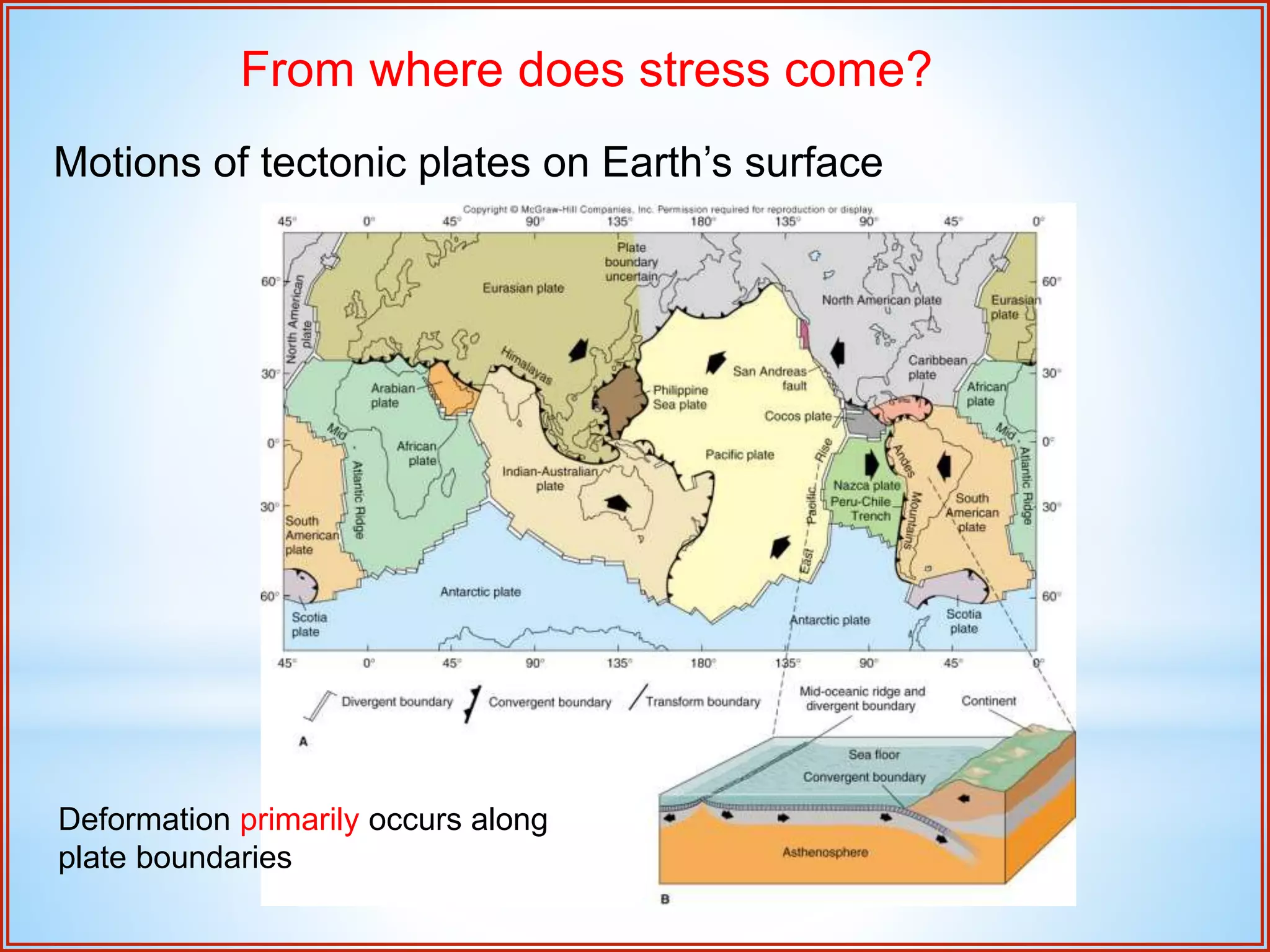
Structural geology is the study of the architecture and geometry of the Earth's crust and the processes that have shaped it. It involves analyzing how rock bodies deform in response to tectonic stresses. Structural analysis generally involves descriptive, kinematic, and dynamic analysis. Descriptive analysis describes rock structures like folds and faults. Kinematic analysis evaluates strain and changes in shape and orientation of rocks. Dynamic analysis reconstructs the stresses that caused rock deformation and failure. Stresses in rocks can be tensile, compressive, or shear stresses. Stress is analyzed using concepts like the stress tensor, Mohr's circle diagrams, and the orientation of maximum shear stresses. The main sources of stress that drive deformation are the motions of tectonic

1. *STRUCTURAL
GEOLOGY
Lecture # 10

2. What is Structural Geology??
• Study of the architecture and geometry of the Earth’s
crust and processes which have shaped it
• Analysis of changes in shape of rock bodies (strain)
produced by tectonic forces (stress)
Stress Strain

3. • Study of rock Deformation as Response to Forces and Stresses
• Involving Motion of Rigid Body

4. Structural Analysis
Structural analysis generally involves three tasks:
1. Descriptive Analysis: physical and geometrical
description of rock structures (e.g. folds, faults etc)
2. Kinematic Analysis: evaluation of the displacement
and
change in shape, orientation and size that rocks undergo
as a result of deformation (strain)
3. Dynamic Analysis: reconstruct forces and stresses
which resulting rock deformation and failure (stress)

5. Deformation of rock in various scale
(Modified from Means, 1976) in Sapiee. B., 2005

6. EVOLUTION OF STRUCTURE
• Force history
• Movement history
Single Particle Particles

7. Factors involve:
• SCALE FACTOR (mm to km)
• RHEOLOGY (flow of matter)
• TIME FACTOR (Geologic Time Scale)

8. Why Important?

9. Geologic Cross-Section
and
Seismic Section
5 Km

10. DESCRIPTIVE ANALYSIS (Fold, Fault)
• CONTACTS
• PRIMARY STRUCTURES
• SECONDARY STRUCTURES

11. Primary Structure
Primary structures are features of rocks
that form at or shortly after the time
of formation of the rock itself.
They are important:
i. to determine to original facing
direction of strata;
ii. can be used as strainmarkers in
deformed rocks;
iii. some primary features (fossils) are
useful in age determination;
iv. interpret the environmet conditions
under which the rock was formed;
v. recognize primary features and
distinguish them from later tectonic
features.
Bedding
• Graded beds
• Ripple marks
• Crossbeds
• Sole marks
• Channel structures
• Mud cracks
• Fossils (tracks, imprints, body fossils)
• Impact features (raindrop imprints,
volcanic bombs etc)
• De-watering (flame) structures
• Soft-sediment deformation
• Reduction spots
Igneous structures
• Columnar jointing
• Flow surface features (rubble layers,
ropey texture, baked horizons)
• Pillow basalts

12. Secondary Structure
• Secondary rock structures are imposed on rocks by events (such as
compression or stretching) experienced by rocks after their
original formational.
• The structures are most easily observed if the rocks have obvious
primary structures, such as layering formed by successive
episodes of deposition.
• Primary depositional layering is almost always horizontal: it
parallels the general configuration of surface on which deposition
takes place, such as a floodplain or the floor of a lake or ocean. In
consequence, when layers are found that are not horizontal, the
geologist assumes that some force has been exerted upon them
that has destroyed their original horizontality.

13. BASIC CONCEPTS
FORCES AND VECTORS
• Force is any action which alters, or tends to alter
• Newton II law of motion : F = M a
• Unit force : kgm/s2 = newton (N) or dyne = gram cm/s2; N = 105 dynes
(a). Force: vector quantity with magnitude and direction
(b). Resolving by the parallelogram of forces
Modified Price and Cosgrove (1990)
Two Types of Force
• Body Forces (i.e. gravitational force)
• Contact Forces (i.e. loading)

14. • F= m x a , gravitational acceleration: 9.8 m/sec2
•vector quantity: orientation and size.
•can be applied to any plane.
•normal and shear components on a plane can be resolved from an oblique
force (see diagram to the right).
•shear component promotes slip on the plane and the normal component
inhibits slip on a plane, and the ratio of the two at which slip occurs
describes the 'friction' on the plane.
Pressure within a geologic context:
•describes multitude of forces at a point within a fluid.
•limit of F/area as area goes to 0
•fluids can not withstand a shear stress for a significant period of time,
therefore if static non-flowing, all force vectors equal in size, and all must
be normal vectors acting perpendicular to any given plane. Hence can be
described by one number.
•this is a special simple stress state - hydrostatic stress state.
•geologic pressures: pore fluid pressures, magmatic pressures, 'rock
pressure' = nondeviatoric component.
•related strain? change in volume, no distortion (unless material is
anisotropic with respect to mechanical properties).

15. Force
Equilibrium
(A) Balance
(B) Torque
(C) Static Equilibrium
(D) Dynamic Equilibrium
(Davis and Reynolds, 1996)

16. STRESS
Stress defined as force per unit area:
s = F/A
A = area,
Stress units = Psi, Newton (N),
Pascal (Pa) or bar (105 Pa)
Stress is force/area
(hitting with a hammer)
Importance of area:
Think of difference between
standing on water bed in high
heels or sneakers

17. Stress
Three kinds of stress can be applied to rocks:
tensional, compressive, and shear.
Tensional stress occurs when a rock is subjected to forces that tend
to elongate it or pull it apart; a rock that has experienced tensional
stress tends to be narrower and longer than its original shape, like a
piece of gum or taffy that has been pulled (pulled apart)
A compressive stress on a rock is applied from opposite sides and
has a tendency to shorten (compress) the rock between the
opposing stresses, which may also stretch it parallel to the stress-free
direction. (push together)
A shear stress results when forces from opposite directions create
a shear plane in an area in which the forces run parallel to one
another. The scale of shear stress can vary from a few centimeters
to hundreds of meters. (moved horizontally past each other)

18. • Stress at a point in 2D
• Types of stress
Stress (s)
Normal stress (sN)
(+) Compressive (-) Tensile
Shear stress (sS)
(+) (-)
Sapiee. B.,
2005

19. STRESS on PLANE
• Coordinate System

20. Stress Ellipsoid
a) Triaxial stress
b) Principal planes of
the ellipsoid
(Modified from Means, 1976) in Sapiee. B., 2005

21. z s
s3 x
X1
Arbitrary coordinate
axes and planes
B. Principal stress components
s(top)
zx
C. General stress components
X
Principal coordinate
axes and planes
Z
s
s

(lft)
xx
(lft)
x
(top)
zz
s
dx
s (bot)
zz
dz
s(rt)
xz
(bot)
z
s(rt)
xx
s(bot)
zx
(lft)
xz
s
(rt)
x
X3
s3
(top)
z
A. Stress elipse
The State of
Two-Dimensional
Stress at Point
(Twiss and Moores, 1992)
Principal Stress:
s1 > s3
x, z = Surface Stress

22. The State of
3-Dimensional
Stress at Point Principal Stress:
s
z
x1
x
s3
B. Principal stress components
x3
y
A. Stress elipsoid
y x2
x
x
y
z
s
x
szy
syx
z
szz
sxy syy
syz
sxx
szx
sxz
y
Arbitrary
coordinate planes
C. General stress components
z
Principal
coordinate planes
s1 > s > s3
Stress Tensor Notation
s11 s12 s13
s = s21 s22 s23
s31 s32 s33
s12 = s21, s13 = s31, s23 = s32
(Twiss and Moores, 1992)

23. Geologic Sign
Convention of
Stress Tensor
(Twiss and Moores, 1992)

24. sn
A. Physical Diagram A. Mohr Diagram
r
n
(p) s  s
(p)
(p)
Mohr Diagram 2-D
(p) s  s
(p) sn
s  s
2
2
s s   3
2
sn
s s   3
sn ,
s
s s  
  3 cos
2
s s  
  3 sin
ss
x  3
s(p) n
s3

s
Plane P
x
s3
(Twiss and Moores, 1992)

25. A. Physical Diagram B. Mohr Diagram

x3
n'
p
(p')

p'
n
x1


(p')
sn ,
ss
sn

s  s
s
sn
s3
(p) sn ,
(p)s  s

(Twiss and Moores, 1992)

26. A. Physical Diagram B. Mohr Diagram
s s  xx' xz

sxx
s s  zz' zx
s s  xx zz
2
s s  xx zz
ss
sxz
s sn
 º)
 s
s3
szz
szx
z
s3

x3
x1
x
sxz
º)

(Twiss and Moores, 1992)

27. Planes of maximum shear stress
A. Physical Diagram B. Mohr Diagram
n-
Planes of maximum
shear stress
x3
Clockwise
shear stress
x
ss ss
Counterclockwise
shear stress
' = +45º
s
x3 s3
s
n+
ss
x
 = +45º
s  s max
Counter clockwise
s s3
 º sn
s  s max
Clockwise
'º
s3
(Twiss and Moores, 1992)

28. Mohr Diagram 3-D
(Twiss and Moores, 1992)
Geometry of a three-dimensional
Stress on a Mohr diagram

29. Maximum Shear Stress
(Twiss and Moores, 1992)

30. FUNDAMENTAL STRESS EQUATIONS
Stress Ellipsoid
Principal Stress:
s1 > s > s3
• All stress axes are mutually perpendicular
• Shear stress are zero in the direction of
principal stress
s1 + s3 - s1 – s3
sN = cos 2
2 2
s1 – s3
ss = Sin 2
2

31. (Davis and Reynolds, 1996)
Mohr diagram is a graphical representative of state of stress
Mean stress is hydrostatic component which tends to produce dilation
Deviatoric stress is non hydrostatic which tends to produce distortion
Differential stress if greater is potential for distortion

32. Image of Stress
a 0 0
0
0
0
0
0 0 0
a 0 0
b
c
0
0 0
A. Hydrostatic stress B. Uniaxial compression C. Uniaxial tension
0
a
b
0
0 0
0
a
p 0 0
0 p 0
0 0 p
a 0 0
b
b
0
0 0
0 0 0
0 0 -a
ss
s s3
D. Axial or confined F. Triaxial stress
compression
E. Axial extension or
extensional stress
sn
p
ss
sn
ss
s s s   3
s
0
0
s s  3
sn s
ss
s s  
sn s3
s
s3
0
ss
sn s3 s3 s3
0
0
ss
sn
s

33. 0
0 0 0
0 0 -a
Deviatoric Applied
0   s s s  n 0
0
a
ss
 3 s
sn
  s
sn
s s3 sn
ss
s3
0
 3 s
s s 3 n
=
0
ss
s sn s3 s
Effective
s3 s s3 s sn
Ds Ds Ds
Dss s  3
ss
s sn
s
s
s3
Es 
0 0 0
s   pf
Es 3 Es 
pf
0 0 =
Es 
Es 
0
0 Es 3
0
0
0 s  p3 f
0
0
s   pf
Applied
G. Pure shear stress H. Deviatoric stress
(two-dimensional)
I. Differential stress
(Three examples)
J. Effective stress

34. From where does stress come?
Motions of tectonic plates on Earth’s surface
Deformation primarily occurs along
plate boundaries

36. STRESS
 Body force works from distance and depends on the amount of materials
affected (i.e. gravitational force).
 Surface force are classes as compressive or tensile according to the
distortion they produce.
 Stress is defined as force per unit area.
 Stress at the point can be divided as normal and shear component
depending they direction relative to the plane.
 Structural geology assumed that force at point are isotropic and
homogenous
 Stress vector around a point in 3-D as stress ellipsoid which have three
orthogonal principal directions of stress and three principal planes.
 Principal stress s1>s2>s3
 The inequant shape of the ellipsoid has to do with forces in rock and has
nothing directly to do with distortions.
 Mohr diagram is a graphical representative of state of stress of rock