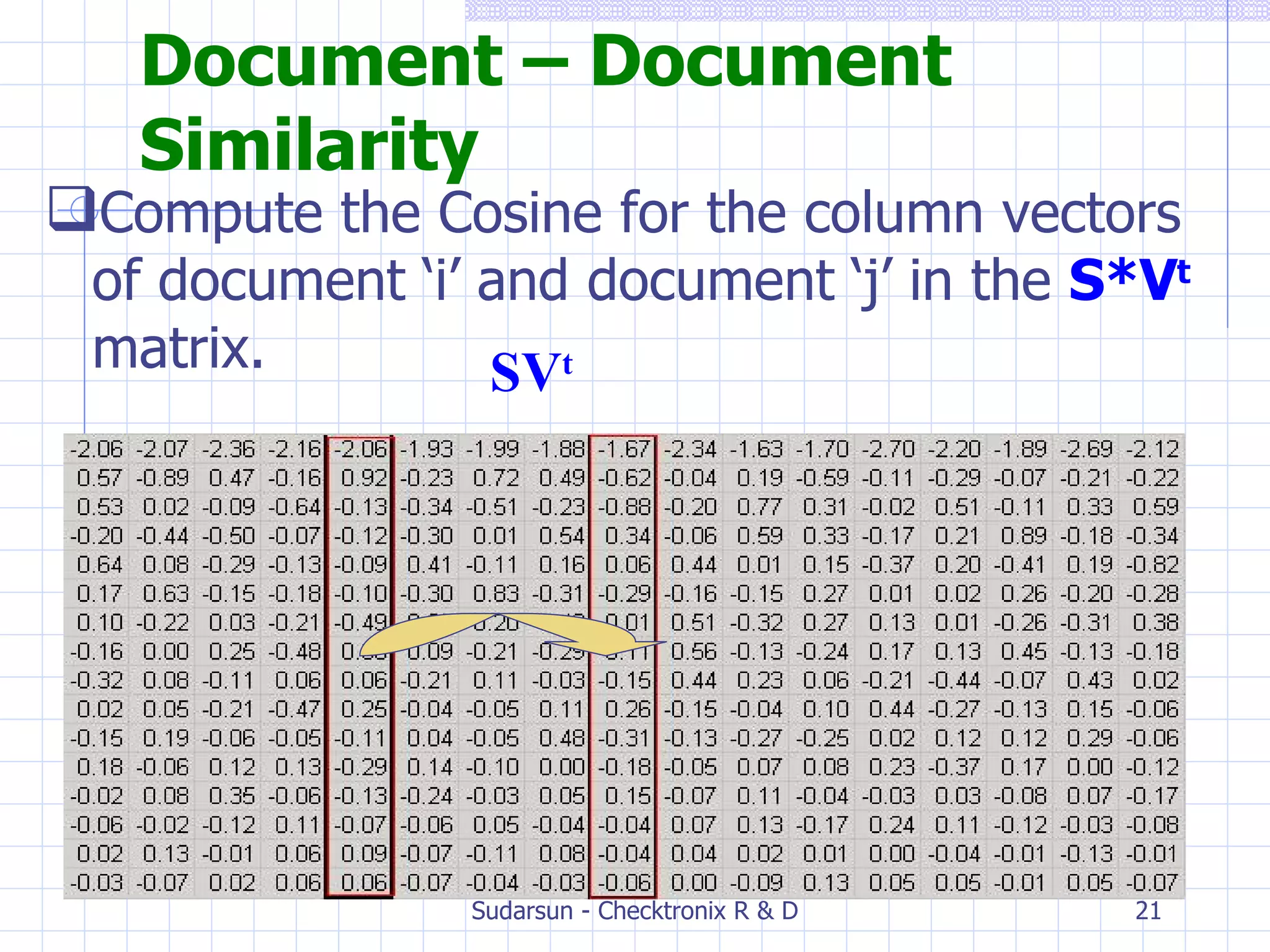
The document discusses Latent Semantic Analysis (LSA), a statistical method for analyzing relationships between documents and terms by reducing large datasets into significant information. It explains concepts such as singular value decomposition, semantic representation, and methods for computing term-document similarities. Additionally, it addresses limitations of LSA and mentions alternative techniques like Probabilistic LSA and Latent Dirichlet Allocation.

1. Latent Semantic Indexing Sudarsun. S., M.Tech Checktronix India Pvt Ltd, Chennai 600034 [email_address]

2. What is NLP ? What is Natural Language ? Can a machine understand NL ? How are we understanding NL ? How can we make a machine understand NL ? What are the limitations ?

3. Major Entities … What is Syntactic Analysis ? Deal Synonymy Deal Polysemy ? What is Semantics ? Represent meanings as a Semantic Net What is Knowledge ? How to represent knowledge ? What are Inferences and Reasoning ? How to use the accumulated knowledge ?

4. LSA for Information Retrieval What is LSA? Singular Value Decomposition Method of LSA Computation of Similarity using Cosine Measuring Similarities Construction of Pseudo-document Limitations of LSA Alternatives to LSA

5. What is LSA A Statistical Method that provides a way to describe the underlying structure of texts Used in author recognition, search engines, detecting plagiarism, and comparing texts for similarities The contexts in which a certain word exists or does not exist determine the similarity of the documents Closely models human learning, especially the manner in which people learn a language and acquire a vocabulary

6. Multivariate Data Reduction technique. Reduces large dataset to a concentrated dataset containing only the significant information from the original data . Singular Value Decomposition

7. Mathematical Background of SVD SVD decomposes a matrix as a product of 3 matrices. Let A be matrix of m x n, then SVD of A is SVD(A) = U MxK S KxK V t KxN U, V  Left and Right Singular matrices respectively U and V are Orthogonal matrix whose vectors are of unit length S  Diagonal matrix whose diagonal elements are Singular Values arranged in descending order K  Rank of A; K<=min(M,N).

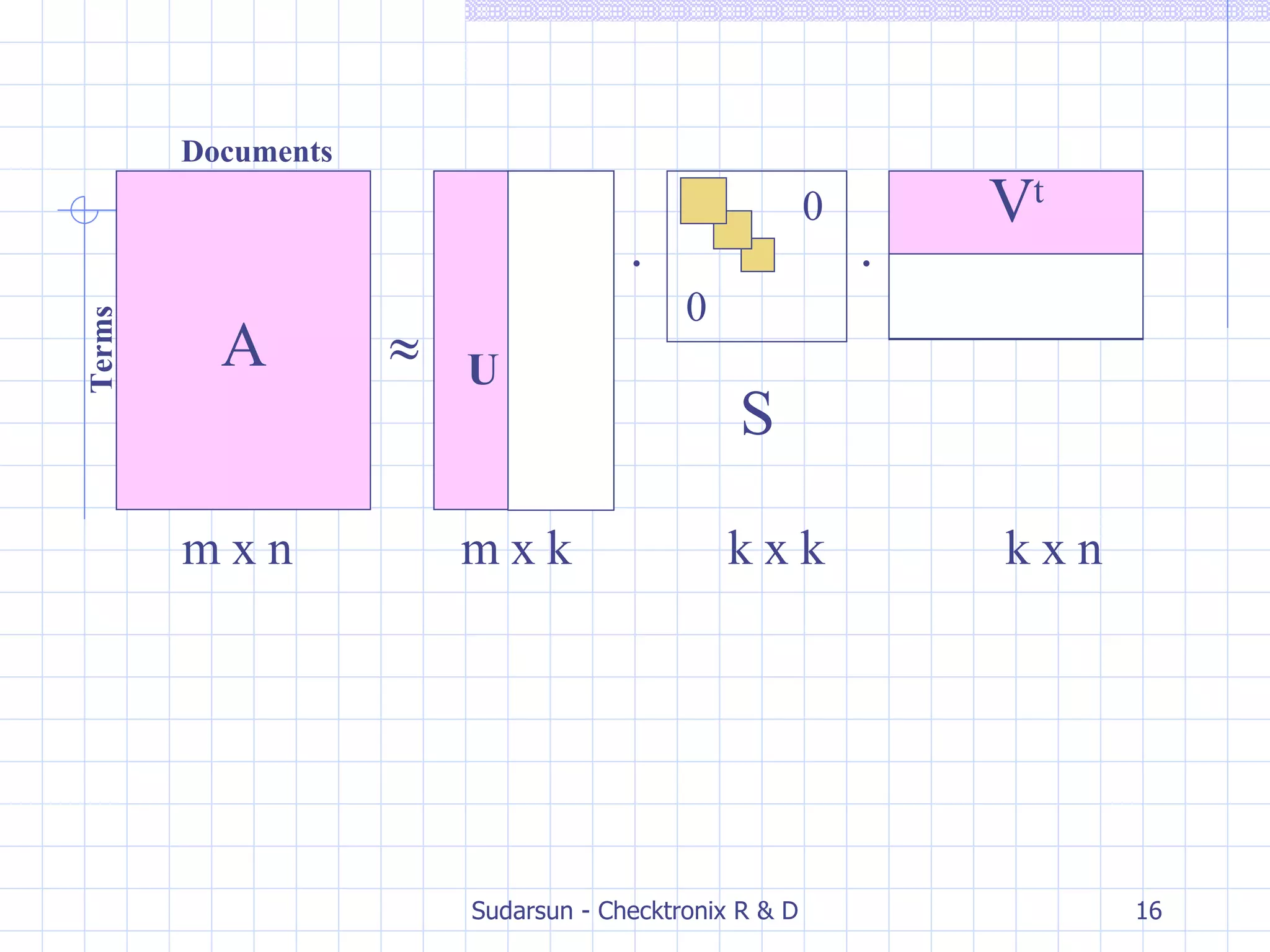
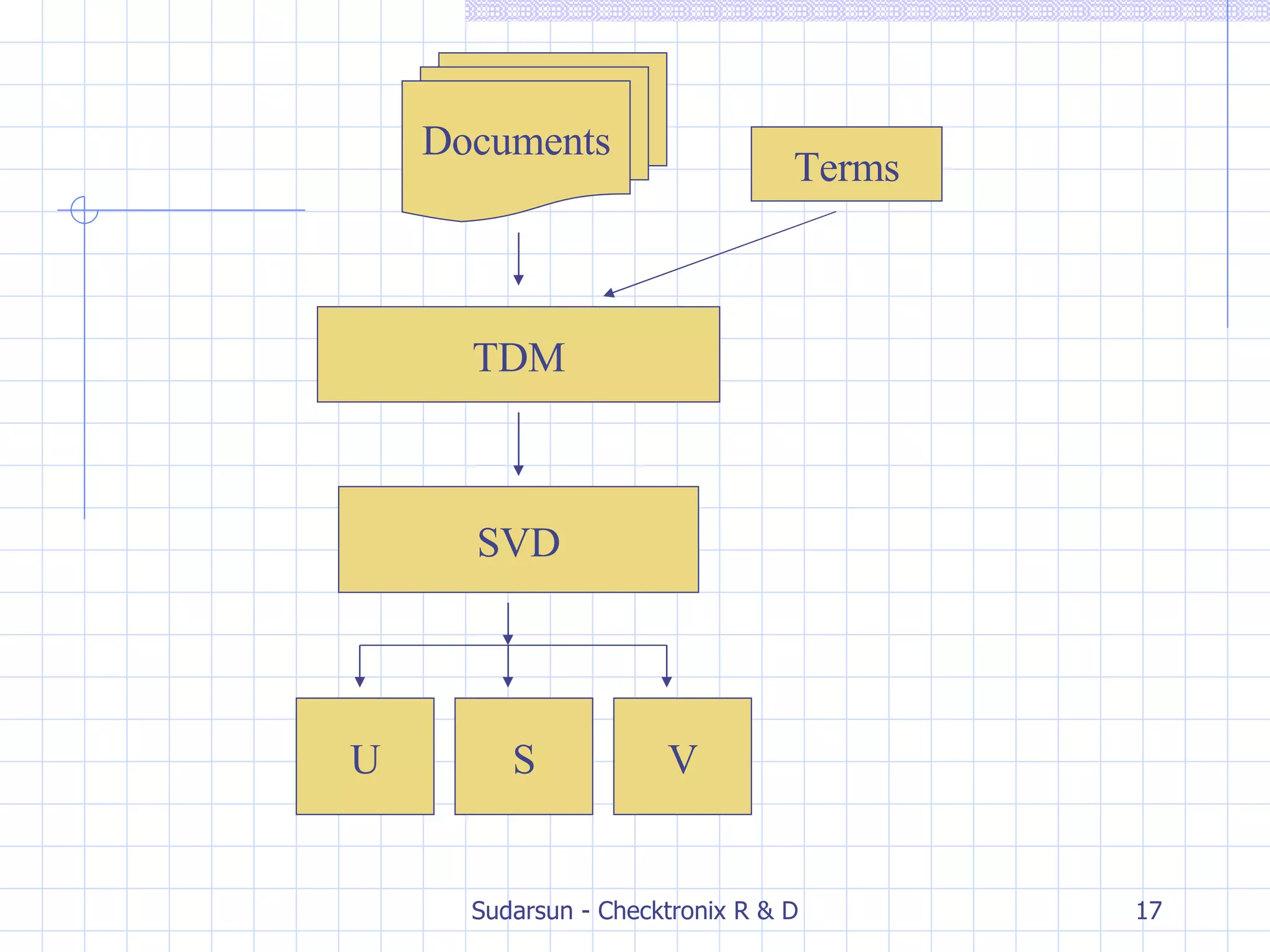
8. Computation of SVD To Find U,S and V matrices Find Eigen Values and their corresponding Eigen Vectors of the matrix AA t Singular values = Square root of Eigen Values. These Singular values arranged in descending order forms the diagonal elements of the diagonal matrix S . Divide each Eigen vector by its length. These Eigen vectors forms the columns of the matrix U . Similarly Eigen Vectors of the matrix A t A forms the columns of matrix V. [ Note : Eigen Values of AA t and A t A are equal.]

9. Eigen Value & Vectors A scalar Lamba is called an Eigen Value of a matrix A if there is a non-zero vector V such that A.V = Lamba.V. This non-zero vector is the Eigen vector of A. Eigen values can be found by solving the equation | A – Lamba.I | = 0.

10. How to Build LSA ? Preprocess the document collection Stemming Stop words removal Build Frequency Matrix Apply Pre-weights Decompose FM into U, S, V Project Queries

11. Step #1: Construct the term-document matrix; TDM One column for each document One row for every word The value of cell (i, j) is the frequency of word i in document j Frequency Matrix

14. Step #2: Weight Functions Increase the efficiency of the information retrieval. Allocates weights to the terms based on their occurrences. Each element is replaced with the product of a Local Weight Function(LWF) and a Global Weight Function(GWF) . LWF considers the frequency of a word within a particular text GWF examines a term’s frequency across all the documents. Pre-weightings Applied on the TDM before computing SVD. Post-weightings Applied to terms of a query when projected for matching or searching.

15. Step #3: SVD Perform SVD on term-document matrix X. SVD removes noise or infrequent words that do not help to classify a document. Octave/Mat lab can be used [u, s, v] = svd(A);

16. A U S V t m x n m x k k x k k x n · ·  Terms Documents 0 0

17. Documents TDM SVD Terms U S V

18. Similarity Computation Using Cosine Consider 2 vectors A & B. Similarity between these 2 vectors is A.B CosØ = ------------------ |A|. |B| CosØ ranges between –1 to +1

19. Similarity Computations in LSA

20. Term-term Similarity Compute the Cosine for the row vectors of term ‘i’ and term ‘j’ in the U*S matrix. US

21. Document – Document Similarity Compute the Cosine for the column vectors of document ‘i’ and document ‘j’ in the S*V t matrix. SV t

22. Term – Document Similarity Compute Cosine between row vector of term ‘i’ in U*S 1/2 matrix and column vector of document ‘j’ in S 1/2 *V t matrix.

23. U*S 1/2 S 1/2 *V t

24. Construction of Pseudo-document A Query is broken in to terms and represented as a column vector (say ‘ q ’ ) consisting of ‘M’ terms as rows. Then Pseudo-document ( Q ) for the query( q ) can be constructed with the help of following mathematical formula. Q = qt*U*S -1 After constructing the Pseudo-document, we can compute the similarities of query-term, query-document using earlier mentioned techniques.

25. Alternatives to LSA LSA is limited to Synonymy problem PLSA – Probabilistic Latent Semantic Analysis to handle Polysemy. LDA – Latent Dirichlet Allocation.

26. References http://www.cs.utk.edu/~lsi/papers/ http://www.cs.utk.edu/~berry/lsi++ http://people.csail.mit.edu/fergus/iccv2005/bagwords.html http://research.nitle.org/lsi/lsa_explanation.htm http://en.wikipedia.org/wiki/Latent_semantic_analysis http://www-psych.nmsu.edu/~pfoltz/reprints/BRMIC96.html http://www.pcug.org.au/~jdowling/ http://www.ucl.ac.uk/oncology/MicroCore/HTML_resource/PCA_1.htm http://public.lanl.gov/mewall/kluwer2002.html http://www.cs.utexas.edu/users/suvrit/work/progs/ssvd.html

27. Thanks.. You may send in your queries to sudar@burning-glass.com