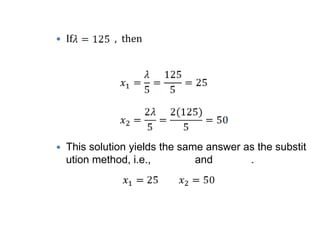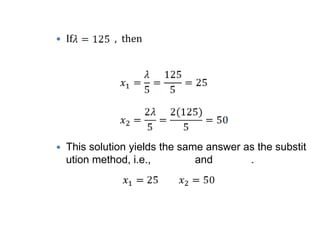
Lagrange's method solves constrained optimization problems by forming an augmented function that combines the objective function and constraints, using Lagrange multipliers (λ) as weighting factors. The method finds extrema by taking partial derivatives of the augmented function with respect to the objective variables and λ, setting the results equal to zero. This produces a system of equations that can be solved simultaneously to identify values that satisfy the constraint and optimize the original objective function.

1. LAGRANGE’S MULTIPLIERS
METHOD

2. Lagrange Multipliers
 The constrained optima problem can be stated as find
ing the extreme value of
subject to .
 So Lagrange (a mathematician) formed the augmente
d function.
denotes augmented function
will behave like the function if the constraint is followed.

3.  Given the augmented function, the first order conditi
on for optimization (where the independent variable
s are , and λ) is as follows:

4.  Using the previous example:
note:
to be on the b
udget line

5. Lagrange Multipliers
 Solving these 3 equations simultaneously:

6.  Solving these 3 equations simultaneously (cont’d):

7.  Solving these 3 equations simultaneously (cont’d):

8.  If , then
 This solution yields the same answer as the substit
ution method, i.e., and .