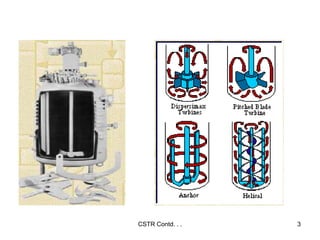
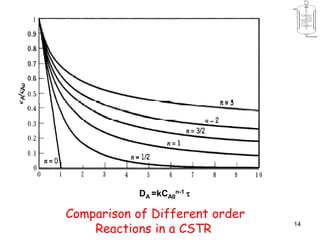
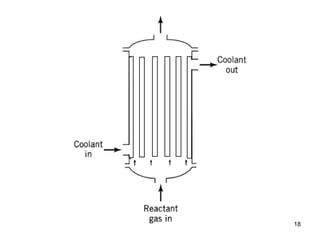
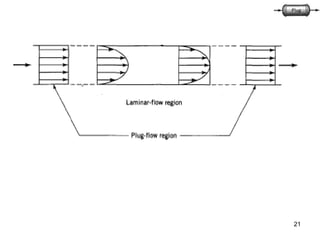
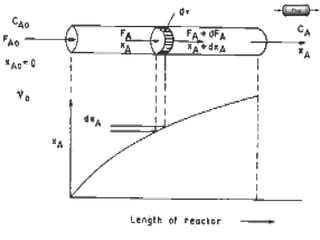
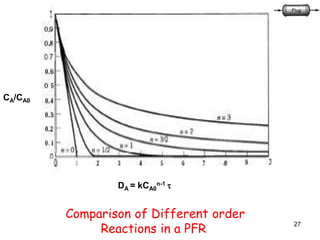
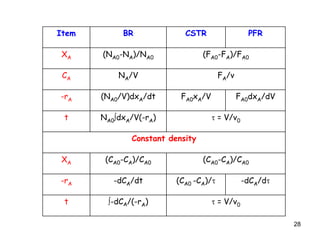
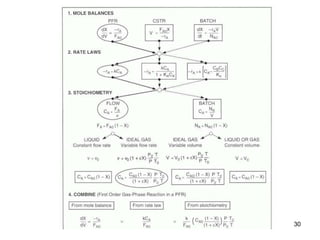
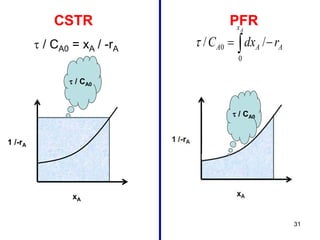
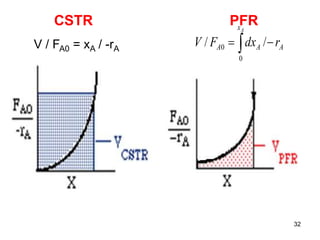
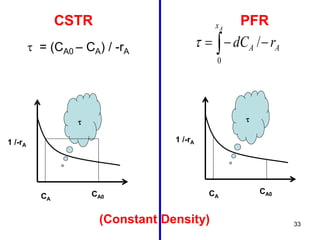
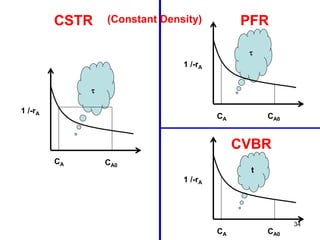
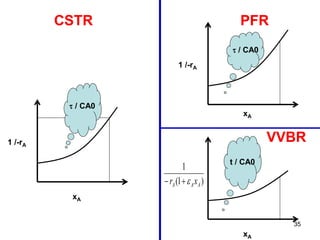
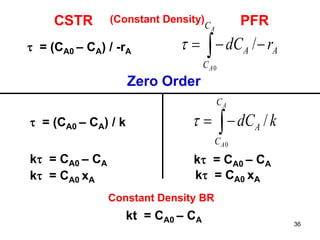
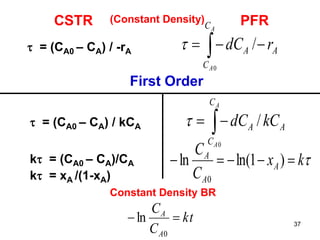
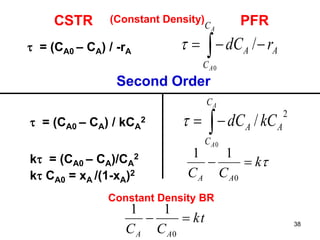
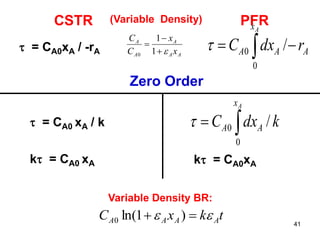
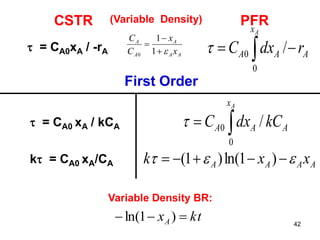
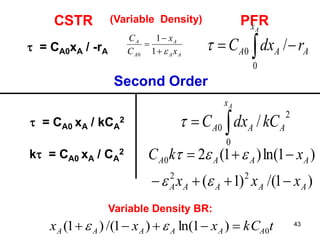
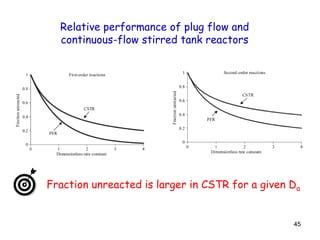
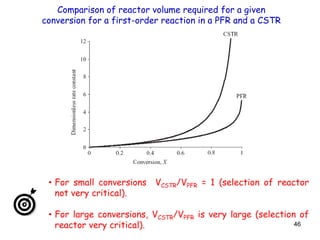
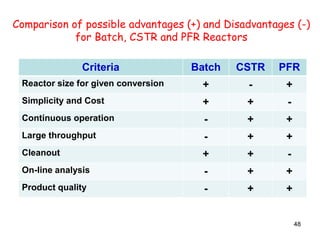
The document discusses continuous ideal reactors, focusing on Continuous Stirred Tank Reactors (CSTR) and Plug Flow Reactors (PFR). It outlines their operating principles, advantages, disadvantages, and performance comparisons under various conditions, emphasizing the differences in reactor design and conversion efficiency. Key parameters such as space time, mean residence time, and orders of reaction are also analyzed to highlight their influence on reactor performance.

1. 1
CONTINUOUS IDEAL
REACTORS

2. 2
Continuous Stirred Tank Reactor

3. CSTR Contd. . . 3

4. CSTR Animation 4

5. CSTR Contd. . . 5
• Also called as Mixed, Backmix, Ideal stirred tank reactor
• Open system, operates under steady state conditions
• Reactants are continuously introduced and products are
continuously withdrawn
• Perfect mixing – contents have uniform properties
– No spatial variations
• Conditions at the exit are same as inside the reactor
• Used for homogenous liquid phase reactions where
constant agitation is required
• Eg. Sulfonation, Polymerization, plastics, explosives,
synthetic rubber etc.

6. CSTR Contd. . . 6
Advantages:
• Cheap to construct
• Good temperature control
• Reactor has large heat capacity
• Easy access to interiors
Disadvantages:
• Conversion per unit volume of the reactor is
smallest compared to other flow reactors

7. 7
Fractional Conversion (xA):
0
0
A
AA
A
F
FF
x


0
0
A
AA
A
C
CC
x


Space time ():
Space time is the time required to process one
reactor volume of inlet material (feed) measured
at inlet conditions.  is the time required for a
volume of feed equal to the volume of the vessel
(V) to flow through the vessel.
 = V/v0 = sec
N.B. : Volume of vessel here means volume of Reaction Mixture.
(for constant density)

8. 8
Space Velocity (S):
Space velocity (S) is the reciprocal of space time,
the number of reactor volumes of feed, measured
at inlet conditions, processed per unit time.
Mean Residence time tm:
The residence time is the length of time species
spend in the reactor. All molecules that enter may
not spend the same time in the reactor.
The distribution of residence times – RTD
The average length of time that molecules spend in
the reactor – mean residence time (tm)
tm = V/vE

9. 9
)1(0 AAA xFF 
000 / AA CFv  lit
molmollit

secsec
For constant density:
)1(
)1(
0
0
0
AA
AAA
A xC
v
xF
v
F
C 


For variable density:
)1(
)1(
)1(
)1(
0
0
0
AA
A
A
AA
AAA
A
x
x
C
xv
xF
v
F
C
 






10. 10
Stoichiometric Table – Flow Systems
B FB0 -(b/a)FA0xA FB= FA0(MB-(b/a)xA)
R FR0 +(r/a)FA0xA FR= FA0(MR+(r/a)xA)
S FS0 +(s/a)FA0xA FS= FA0(MS+(s/a)xA)
I FI0 0 FI = FI0
Total FT0 FT = FT0 + NA0δxA
Where: MI = FI0/FA0
δ = (r/a + s/a – b/a – 1)
aA + bB  rR + sS
For Constant density: CA = CA0(1-xA)
Species Initial Change Final moles
A FA0 -FA0xA FA= FA0(1-xA)

11. 11

12. 12
Design Equation
General Mass Balance Equation:
Rate of Input = rate of output + accumulation
+ rate of disappearance
FA0 = FA + 0 + (-rA) V
FA0 - FA = (-rA) V
FA0 xA = (-rA) V
V / FAo = xA / -rA
FA0
CA0
v0
FA
CA
V
xA

13. 13
V / FAo = xA / -rA
General Design eqn. for a CSTR:
V / (v0 CA0) = xA / -rA
 / CA0 = xA / -rA
Design eqn. for a CSTR under constant density:
 = (CA0 – CA) / -rA
tm = V/vE
Note that the space time and the mean
residence time are equal only in the case of
constant density.

14. 14
DA =kCA0
n-1 
Comparison of Different order
Reactions in a CSTR

15. 15
Plug Flow Reactor

16. PFR Animation 16
The necessary and sufficient
condition for plug flow is the
residence time in the reactor to
be the same for all elements of
the fluid.

17. 17
• PFR is also called as tubular reactor
• Residence time is same for all fluid elements
• Operated under steady state conditions
• Reactants are consumed as they flow down along the
length of the reactor
• Axial concentration gradients exist
• One long tube or a number of short tubes (see fig.)
• Choice of diameter depends on fabrication cost,
pumping cost and heat transfer needs
• Wide variety of applications in gas/liquid phase
• Eg.: Production of gasoline, cracking, synthesis of
ammonia, SO2 oxidation

18. 18

19. 19
(1) The flow in the vessel is Plug flow.
(2)There is no axial mixing of fluid inside the
vessel (i.e., in the direction of flow).
(3)There is complete radial mixing of fluid inside
the vessel (i.e., in the plane perpendicular to
the direction of flow).
(4)Properties may change continuously in the
direction of flow
(5)In the axial direction, each portion of fluid,
acts as a closed system in motion, not
exchanging material with the portion ahead of
it or behind it.

20. PFR Contd. . . 20
Advantages:
• Easily maintained as there are no moving parts
• High conversion per unit volume
• Unvarying product quality
• Good for studying rapid reactions
Disadvantages:
• Poor temperature control
• Hot spots may occur when used for exothermic
reactions

21. 21

22. 22

23. 23

24. 24
Design Equation
General Mass Balance Equation:
Rate of Input = rate of output + accumulation
+ rate of disappearance
FA = FA + dFA + 0 + (-rA) dV
-dFA = (-rA) dV
FA0 dxA = (-rA) dV

25. 25

26. 26
 
Ax
AAA rdxFV
0
0 //
General Design eqn. for a PFR:
 
Ax
AAA rdxC
0
0 //
Design eqn. for a PFR (under constant density):
 
Ax
AA rdC
0
/ 
V
m vdVt
0
/
Note that the space time and the mean
residence time are equal only in the case of
constant density.

27. 27
CA/CA0
DA = kCA0
n-1 
Comparison of Different order
Reactions in a PFR

28. 28
Item BR CSTR PFR
XA (NA0-NA)/NA0 (FA0-FA)/FA0
CA NA/V FA/v
-rA (NA0/V)dxA/dt FA0xA/V FA0dxA/dV
t NA0dxA/V(-rA)  = V/v0
Constant density
XA (CA0-CA)/CA0 (CA0-CA)/CA0
-rA -dCA/dt (CA0 -CA)/ -dCA/d
t -dCA/(-rA)  = V/v0

29. 29
Algorithm for Isothermal Reactor Design

30. 30

31. 31
CSTR PFR
 / CA0 = xA / -rA  
Ax
AAA rdxC
0
0 //
1 /-rA
xA
 / CA0
 / CA0

32. 32
CSTR PFR
V / FA0 = xA / -rA  
Ax
AAA rdxFV
0
0 //

33. 33
CSTR PFR
1 /-rA

 = (CA0 – CA) / -rA  
Ax
AA rdC
0
/
CA
CA0
1 /-rA

CA
CA0
(Constant Density)

34. 34
CSTR PFR
1 /-rA

CA CA0
1 /-rA

CA CA0
(Constant Density)
CVBR
1 /-rA
t
CA CA0

35. 35
CSTR PFR
VVBR1 /-rA
xA
 / CA0
1 /-rA
xA
 / CA0
xA
t / CA0
)1(
1
AAA xr 

36. 36
CSTR PFR
 = (CA0 – CA) / -rA  
A
A
C
C
AA rdC
0
/
(Constant Density)
Zero Order
 = (CA0 – CA) / k 
A
A
C
C
A kdC
0
/
k = CA0 – CA k = CA0 – CA
Constant Density BR
kt = CA0 – CA
k = CA0 xA k = CA0 xA

37. 37
CSTR PFR
 = (CA0 – CA) / -rA  
A
A
C
C
AA rdC
0
/
(Constant Density)
First Order
 = (CA0 – CA) / kCA A
C
C
A CkdC
A
A

0
/
k = (CA0 – CA)/CA
Constant Density BR
kx
C
C
A
A
A
 )1ln(ln
0
kt
C
C
A
A

0
ln
k = xA /(1-xA)

38. 38
CSTR PFR
 = (CA0 – CA) / -rA  
A
A
C
C
AA rdC
0
/
(Constant Density)
Second Order
 = (CA0 – CA) / kCA
2
2
0
/ A
C
C
A CkdC
A
A

k = (CA0 – CA)/CA
2
Constant Density BR
k
CC AA

0
11
kt
CC AA

0
11
k CA0 = xA /(1-xA)2

39. 39
Constant Density

40. 40
For constant density:
• The performance of the Batch reactor is
similar to that of PFR for all orders
• The performance of all the three reactors is
the same in case of zero order reaction
• The performance of PFR is superior to that
of a CSTR for all orders > 0
For all reaction orders > 0
• The volume of a CSTR required for obtaining a
given conversion is larger than that of PFR
• For the same volumes of PFR & CSTR, the
conversion obtained is larger in the case of PFR

41. 41
CSTR PFR
 = CA0xA / -rA  
Ax
AAA rdxC
0
0 /
(Variable Density)
Zero Order
 = CA0 xA / k

Ax
AA kdxC
0
0 /
k = CA0 xA k = CA0xA
Variable Density BR:
tkxC AAAA   )1ln(0
AA
A
A
A
x
x
C
C



1
1
0

42. 42
CSTR PFR
 = CA0xA / -rA
 
Ax
AAA rdxC
0
0 /
(Variable Density)
First Order
 = CA0 xA / kCA A
x
AA CkdxC
A

0
0 /
k = CA0 xA/CA
Variable Density BR:
AAAA xxk   )1ln()1(
ktxA  )1ln(
AA
A
A
A
x
x
C
C



1
1
0

43. 43
CSTR PFR
 = CA0xA / -rA  
Ax
AAA rdxC
0
0 /
(Variable Density)
Second Order
 = CA0 xA / kCA
2
2
0
0 / A
x
AA CkdxC
A

Variable Density BR:
)1ln()1(20 AAAA xkC  
)1/()1( 22
AAAAA xxx  
tkCxxx AAAAAA 0)1ln()1/()1(  
AA
A
A
A
x
x
C
C



1
1
0
k = CA0 xA / CA
2

44. 44
Variable Density

45. 45
Relative performance of plug flow and
continuous-flow stirred tank reactors
Fraction unreacted is larger in CSTR for a given Da

46. 46
Comparison of reactor volume required for a given
conversion for a first-order reaction in a PFR and a CSTR
• For small conversions VCSTR/VPFR = 1 (selection of reactor
not very critical).
• For large conversions, VCSTR/VPFR is very large (selection of
reactor very critical).

47. 47
For Variable density:
• The performance of CSTR & PFR is similar in
case of zero order (irrespective of constant /
variable density)
• The performance of BR is different from the
performance of PFR (the performance was
similar in the case of constant density)
• The performance of PFR is superior to that of
a CSTR for all orders > 0 (same as constant
density)

48. 48
Criteria Batch CSTR PFR
Reactor size for given conversion + - +
Simplicity and Cost + + -
Continuous operation - + +
Large throughput - + +
Cleanout + + -
On-line analysis - + +
Product quality - + +
Comparison of possible advantages (+) and Disadvantages (-)
for Batch, CSTR and PFR Reactors

49. 49
ANY CLARIFICATIONS ?
Abbey, Edward
That which today calls itself science gives us more and more information,
an indigestible glut of information, and less and less understanding.