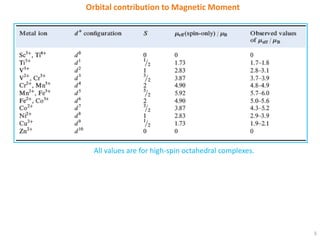
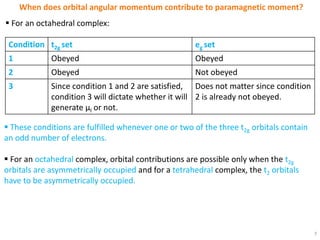
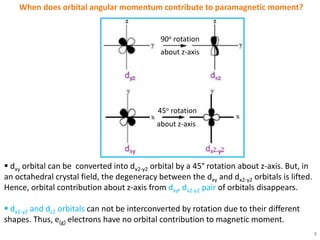
The selection rules that determine which electronic transitions are allowed or forbidden in transition metal complexes are the Laporte selection rule and spin selection rule. The Laporte rule forbids transitions that result in no change in orbital angular momentum, while the spin rule forbids transitions that change the overall spin of the complex. These rules can be relaxed by vibronic coupling in octahedral complexes or do not apply in tetrahedral complexes. Orbital contributions to paramagnetic moment only occur when the transition metal d orbitals are asymmetrically occupied, allowing electron circulation between degenerate orbitals.

1. 1
Selection Rules
 Some transitions are not allowed does not mean that such a transition will never
occur, but that it is less likely and that the intensity (molar absorption coefficient) of
such an absorption band is very low. Whether transitions are allowed or forbidden,
and to what degree they may be forbidden depends on selection rules:
 Laporte Selection Rule: In a molecule having center of symmetry, transitions
between states of the same parity (symmetry with respect to a center of inversion)
are forbidden.
 For example, transitions between states that arise from d orbitals are forbidden
(g→g transitions; d orbitals are symmetric to inversion), but transitions between
states arising from d and p orbitals are allowed (g→u transitions; p orbitals are anti-
symmetric to inversion). Therefore, all d-d transitions in octahedral complexes
are Laporte-forbidden.
 Laporte-allowed transitions involve Δl = ±1.
‘s ↔ p’, ‘p ↔ d’, ‘d ↔ f’ etc allowed (Δl = ±1)
‘s ↔ d’, ‘p ↔ f’ etc forbidden (Δl = ±2)
‘s ↔ s’, ‘p ↔ p’ , ‘d ↔ d’, ‘f ↔ f’ etc forbidden (Δl = 0)

2. 2
▪ Like all chemical bonds, octahedral complexes vibrate in ways (unsymmetrical
vibrations) in which the center of symmetry is temporarily lost. This phenomenon,
called vibronic (vibrational-electronic) coupling, can relax Laporte selection rule.
They are often responsible for the bright colors of these complexes.
▪ In tetrahedral complexes, there is no center of symmetry and thus orbitals have no
g or u designation. Therefore, the Laporte rule does not apply and the complexes
exhibit strong colors.
Relaxation of Laporte Selection Rule
Band Type εmax (L mol-1 cm-1)
Spin forbidden, Laporte forbidden 10-3-1
Spin allowed, Laporte forbidden 1-100
Spin allowed, Laporte allowed 100-1000
Symmetry allowed (charge-transfer bands) 1,000-106
Intensities of Spectroscopic Bands in 3d Complexes

3. 3
Selection Rules
 Spin Selection Rule: The overall spin S of a complex must not change during an
electronic transition, hence, ΔS = 0.
 To be allowed, a transition must involve no change in spin state. This is because
electromagnetic radiation usually cannot change the relative orientation of an
electron spin.
▪ [Mn(H2O)6]2+ has a d5 configuration and it is a high-spin complex. Electronic
transitions are not only Laporte-forbidden, but also spin-forbidden. The dilute
solutions of Mn2+ complexes are therefore colorless.
▪ Certain complexes like MnO4
- and CrO4
2- are intensely colored even though they
have metal ions without electrons in d orbitals. The color of these complexes are not
from d-d transitions, but from charge-transfer from ligand to metal orbitals.

4. 4
Theoretical Paramagnetic Moment
 Paramagnetic moment originates from spin and orbital motion of unpaired
electrons.
▪ When there is significant spin and orbital angular momentum contributions,
theoretical μ is given by:
 The observed value of μ in complexes is always less than the theoretical value
calculated from above equation. This occurs because the ligand field quenches orbital
contribution to some extent. In the extreme case when L = 0, the orbital contribution
to the magnetic moment is said to be quenched.
 When orbital angular momentum is absent, theoretical μ is given by:
 S = n/2 gives spin-only formula:
μS+L
μs.o.
μs.o.

5. 5
Orbital contribution to Magnetic Moment
All values are for high-spin octahedral complexes.

6. 6
When does orbital angular momentum contribute to paramagnetic moment?
 For orbital angular momentum to contribute, there must be an equivalent and
degenerate orbital (similar in energy to that of the orbital occupied by the unpaired
electrons). If this is so, the electrons can make use of the available orbitals to
circulate or move around the center of the complexes and hence generate L and μL
(it is the rotation of the electrons which induces the orbital contribution).
 Essential Conditions:
1) The orbitals should be degenerate (t2g or eg).
2) The orbitals should be similar in shape and size, so that they are transferable into
one another by rotation about the same axis.
3) Orbitals must not contain electrons of identical spin.

7. 7
When does orbital angular momentum contribute to paramagnetic moment?
 These conditions are fulfilled whenever one or two of the three t2g orbitals contain
an odd number of electrons.
 For an octahedral complex, orbital contributions are possible only when the t2g
orbitals are asymmetrically occupied and for a tetrahedral complex, the t2 orbitals
have to be asymmetrically occupied.
 For an octahedral complex:
Condition t2g set eg set
1 Obeyed Obeyed
2 Obeyed Not obeyed
3 Since condition 1 and 2 are satisfied,
condition 3 will dictate whether it will
generate μl or not.
Does not matter since condition
2 is already not obeyed.

8. 8
When does orbital angular momentum contribute to paramagnetic moment?
 dxy orbital can be converted into dx2-y2 orbital by a 45° rotation about z-axis. But, in
an octahedral crystal field, the degeneracy between the dxy and dx2-y2 orbitals is lifted.
Hence, orbital contribution about z-axis from dxy, dx2-y2 pair of orbitals disappears.
 dx2-y2 and dz2 orbitals can not be interconverted by rotation due to their different
shapes. Thus, e(g) electrons have no orbital contribution to magnetic moment.
45o rotation
90o rotation
about z-axis
about z-axis

9. 9
When does orbital angular momentum contribute to paramagnetic moment?
 dxz orbital can be converted into dyz orbital by a 90° rotation about z-axis. Thus, all
t2(g) orbitals may be interconverted by rotation about suitable axes and we may expect
orbital contributions from t2(g) electrons.
 If all the t2g orbitals are singly occupied (t2g
3), an electron in, say, dxz orbital cannot
be transferred into dyz orbital because it already contains an electron having the same
spin quantum number as the incoming electron; if all the t2g orbitals are doubly
occupied (t2g
6), the transfer is not possible.
 Thus, only configurations other than t2g
3 and t2g
6 make orbital contributions to
magnetic moments. For high-spin octahedral complexes, orbital contribution is
expected for: t2g
1, t2g
2, t2g
4eg
2 and t2g
5eg
2.
 For tetrahedral complexes, orbital contribution is expected for: e2t2
1, e2t2
2, e4t2
4
and e4t2
5.