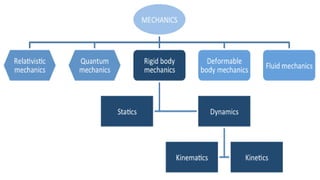
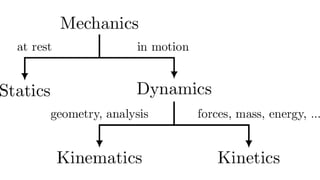
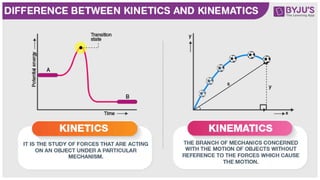
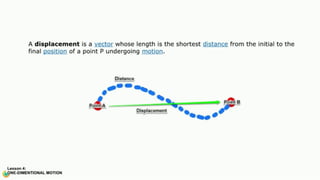
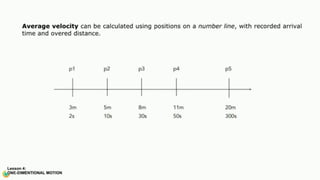
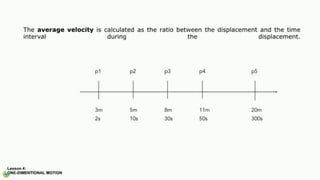
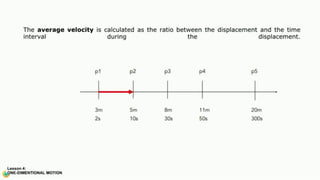
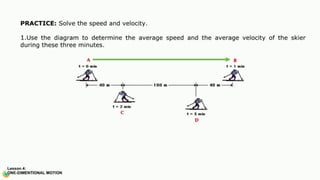
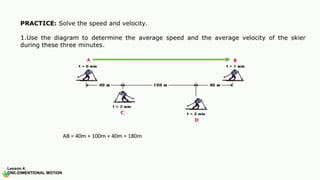
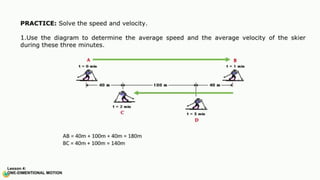
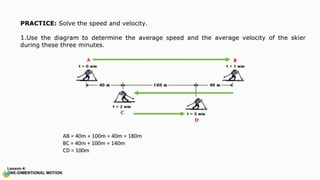
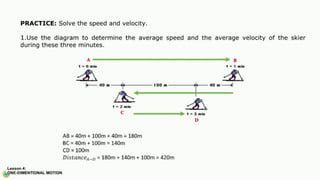
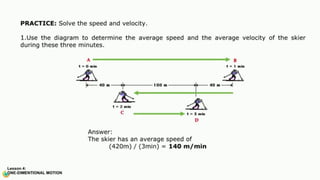
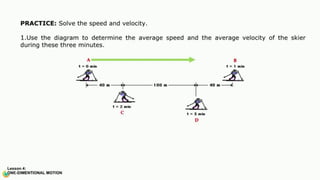
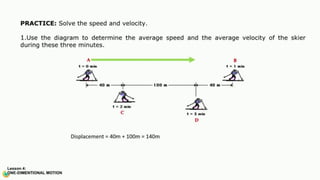
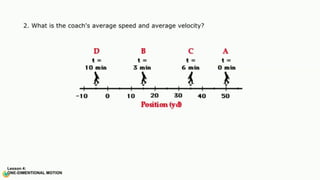
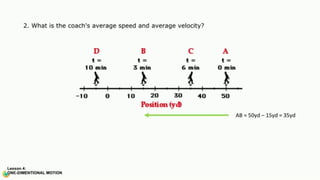
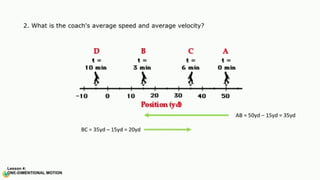
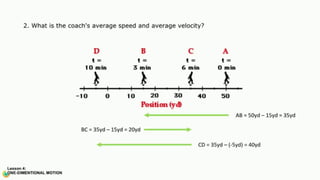
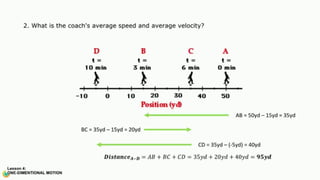
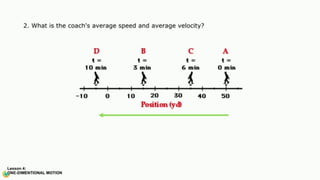
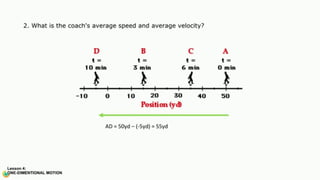
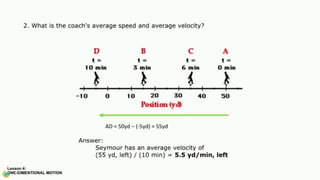
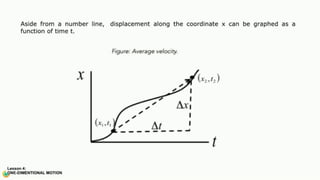
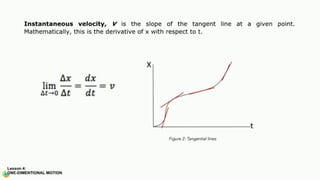
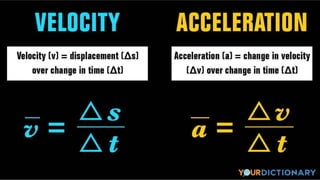
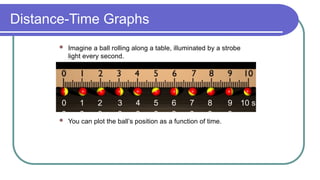
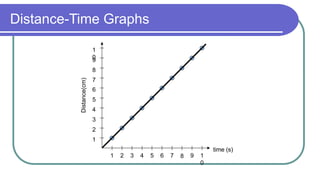
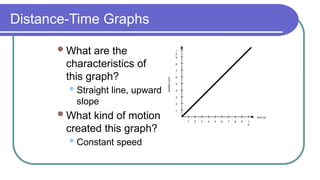
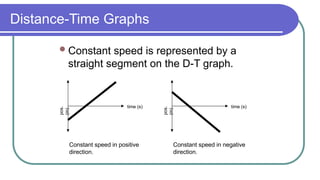
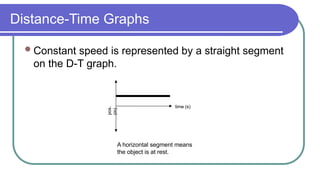
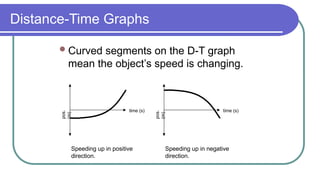
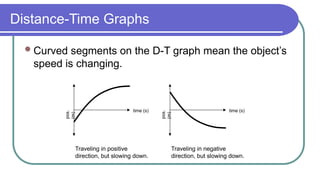
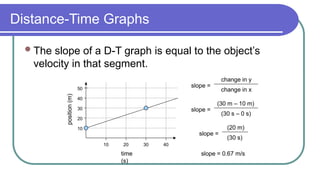
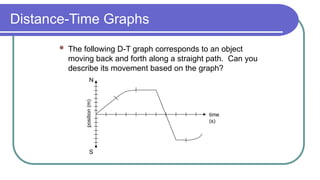
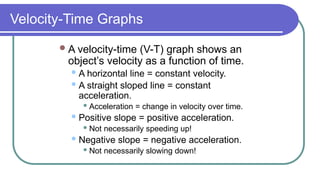
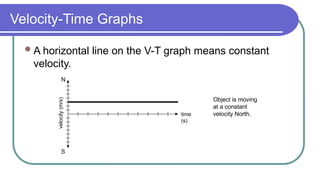
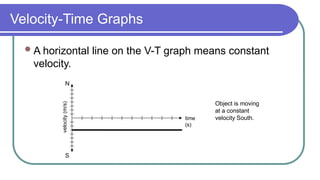
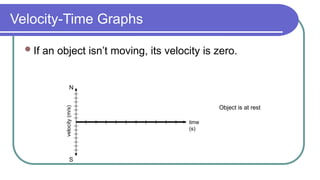
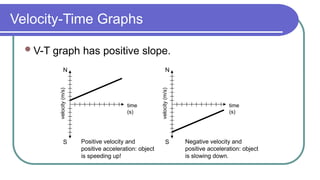
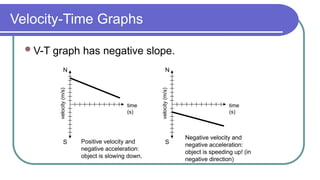
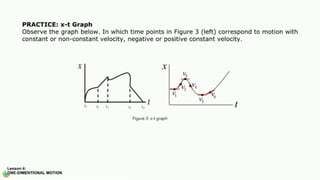
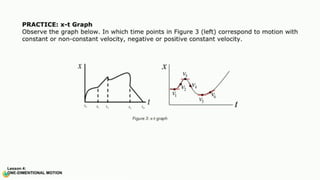
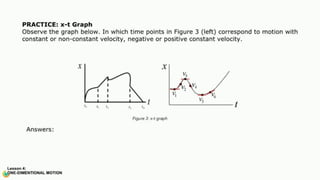
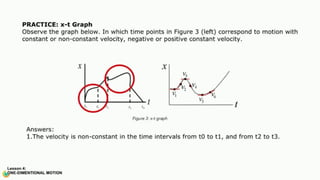
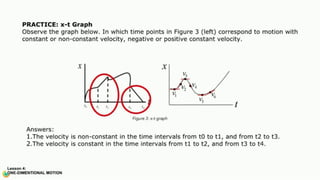
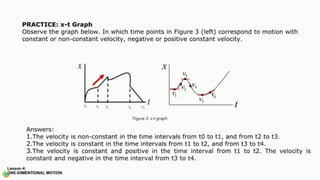
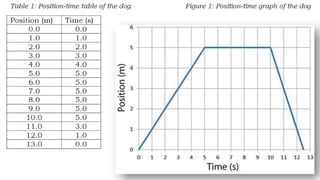
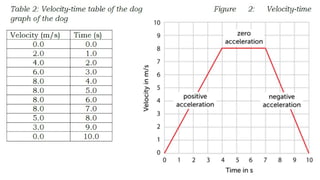
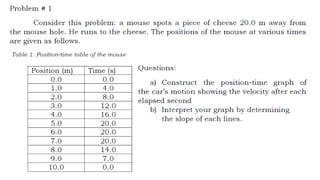
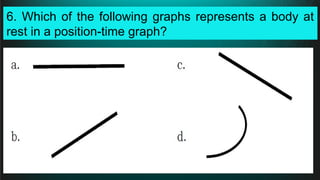
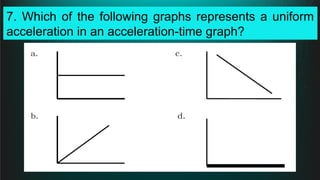
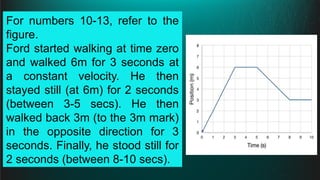
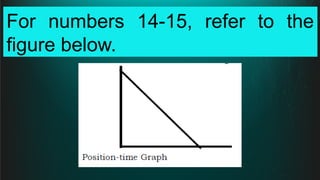
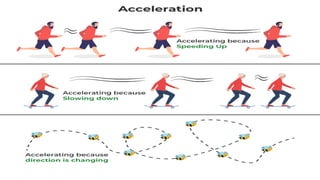
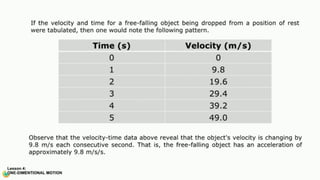
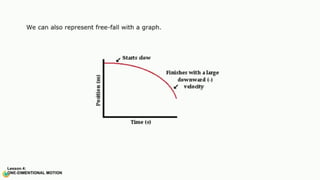
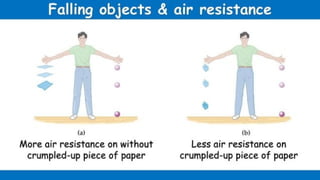
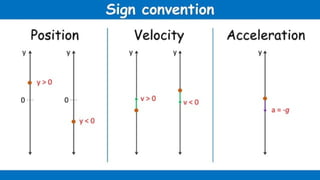
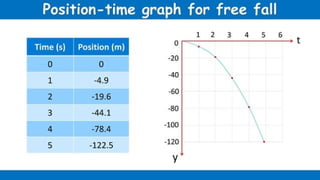
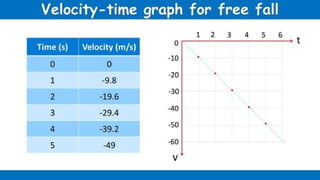
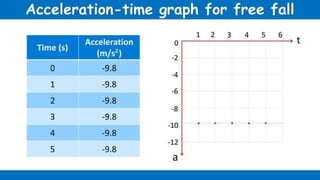
The document contains a series of physics questions and assessments related to concepts of one-dimensional motion, including speed, velocity, distance, displacement, and acceleration. It describes various situations and problems involving calculations of average speed, instantaneous velocity, and graphical representations of motion. Additionally, it covers both theoretical and practical applications of motion concepts, such as the effects of gravity and motion in relation to time.





















































































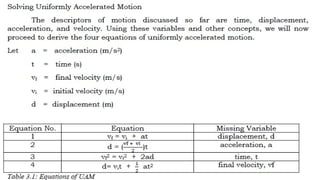











































![9. A car traveling at 22.4 m/s skids to a stop in 2.55 s.
Determine the skidding distance of the car (assume
uniform acceleration).
d = [(vi + vf)/2]t
d = [(22.4 m/s + 0 m/s)/2] 2.55 s
d = (11.2 m/s)(2.55 s)
d = 28.6 m](https://image.slidesharecdn.com/genphy1q1w2-240929152133-fe605c31/85/General-Physics-1-Two-Directional-Motion-pptx-198-320.jpg)



























