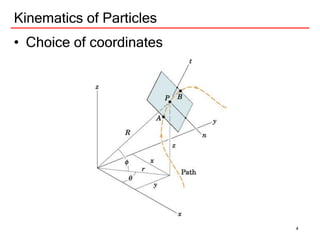
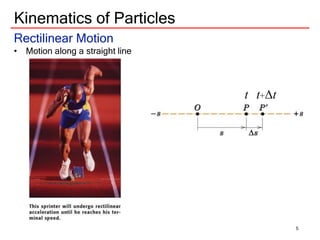
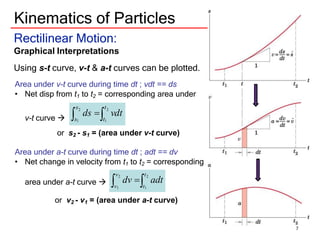
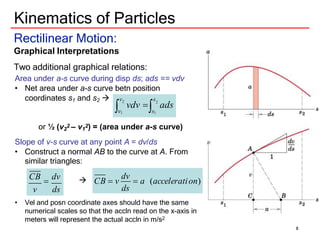
The document discusses kinematics of particles, including rectilinear and curvilinear motion. It defines key concepts like displacement, velocity, and acceleration. It presents equations for calculating these values for rectilinear motion under different conditions of acceleration, such as constant acceleration, acceleration as a function of time, velocity, or displacement. Graphical interpretations are also described. An example problem is worked through to demonstrate finding velocity, acceleration, and displacement at different times for a particle moving in a straight line.

1. ENGINEERING DYNAMICS
Dr. THABIT SALIM NASSOR
Kinematics of Particles

2. Kinematics of Particles
Contents
• Rectilinear motion; Derivation of motion
equations for velocity and acceleration.
• Curvilinear motion in a single plane
• Rectangular coordinates for motion of particle
• Polar coordinates for motion of particle
• Space curvilinear motion in 3D (Velocity and
acceleration)

3. Kinematics of Particles
ME101 - Division III Kaustubh Dasgupta 3
• Motion
– Constrained :: confined to a specific path
– Unconstrained :: not confined to a specific path
• Choice of coordinates
– Position of P at any time t
• rectangular (i.e., Cartesian) coordinates x, y, z
• cylindrical coordinates r, θ, z
• spherical coordinates R, θ, Φ
– Path variables
• Measurements along the tangent t and normal n to
the curve

4. Kinematics of Particles
• Choice of coordinates
4

5. Kinematics of Particles
Rectilinear Motion
• Motion along a straight line
t t+Δt
5

6. •Motion along a straight line
Position at any instance of time t
:: specified by its distance s measured from some convenient reference point O
fixed on the line
:: (disp. is negative if the particle moves in the negative s-direction).
Velocity of the particle: Acceleration of the particle
Kinematics of Particles :: Rectilinear Motion
t t+Δt
+ve or –ve depending
on +ve or –ve displacement
6
Both are
vector quantities
+ve or –ve depending on whether
velocity is increasing or decreasing

7. Kinematics of Particles
Rectilinear Motion:
Graphical Interpretations
Using s-t curve, v-t & a-t curves can be plotted.
Area under v-t curve during time dt ; vdt == ds
• Net disp from t1 to t2 = corresponding area under
v-t curve à
or s2 - s1 = (area under v-t curve)
Area under a-t curve during time dt ; adt == dv
• Net change in velocity from t1 to t2 = corresponding
area under a-t curve à
or v2 - v1 = (area under a-t curve)
ò
ò
2
2
s t
s1 t1
ds = vdt
ò
7
ò
2
2
v t
v1 t1
dv = adt

8. Kinematics of Particles
Rectilinear Motion:
Graphical Interpretations
Two additional graphical relations:
Area under a-s curve during disp ds; ads == vdv
• Net area under a-s curve betn position
coordinates s1 and s2 à
or ½ (v2
2 – v1
2) = (area under a-s curve)
Slope of v-s curve at any point A = dv/ds
• Construct a normal AB to the curve at A. From
similar triangles:
à
• Vel and posn coordinate axes should have the same
numerical scales so that the accln read on the x-axis in
meters will represent the actual accln in m/s2
ò
ò
2 s
s1
v
v1
vdv = 2
ads
v ds
CB
=
dv CB = v
dv
= a (acceleration)
ds
8

9. Kinematics of Particles :: Rectilinear Motion
Analytical Integration to find the position coordinate
Acceleration may be specified as a function of time, velocity, or position
coordinate, or as a combined function of these.
(a) Constant Acceleration
At the beginning of the interval à t = 0, s = s0, v = v0
For a time interval t: integrating the following two equations
Substituting in the following equation and integrating will give the position
coordinate:
Equations applicable for Constant Acceleration and for time interval 0 to t
v =
ds
dt
a = dv
dt
vdv = ads
9

10. Kinematics of Particles :: Rectilinear Motion
Analytical Integration to find the position coordinate
(b) Acceleration given as a function of time, a = f(t)
At the beginning of the interval à t = 0, s = s0, v = v0
For a time interval t: integrating the following equation
à
Substituting in the following equation and integrating will give the position
coordinate:
Alternatively, following second order differential equation may be solved to
get the position coordinate:
v =
ds
dt
a =
dv
dt
f (t) =
dv
dt
10

11. Kinematics of Particles :: Rectilinear Motion
Analytical Integration to find the position coordinate
(c) Acceleration given as a function of velocity, a = f(v)
At the beginning of the interval à t = 0, s = s0, v = v0
For a time interval t: Substituting a and integrating the following equation
à
Solve for v as a function of t and integrate the following equation to get the
position coordinate:
Alternatively, substitute a = f(v) in the following equation and integrate to
get the position coordinate :
v = ds
dt
a = dv
dt
f (v) =
dv
dt
vdv = ads
11

12. Kinematics of Particles: Rectilinear Motion
Analytical Integration to find the position coordinate
(d) Acceleration given as a function of displacement, a = f(s)
At the beginning of the interval à t = 0, s = s0, v = v0
For a time interval t: substituting a and integrating the following equation
Solve for v as a function of s : v = g(s), substitute in the following equation
and integrate to get the position coordinate:
It gives t as a function of s. Rearrange to obtain s as a function of t to get
the position coordinate.
In all these cases, if integration is difficult, graphical, analytical, or
computer methods can be utilized.
v = ds
dt
vdv = ads
12

13. Kinematics of Particles: Rectilinear Motion
13
Example
Position coordinate of a particle confined to move along a straight line is given by
s = 2t3 – 24t + 6, where s is measured in meters from a convenient origin and t is
in seconds. Determine: (a) time reqd for the particle to reach a velocity of 72 m/s
from its initial condition at t = 0, (b) acceleration of the particle when v = 30 m/s,
and (c) net disp of the particle during the interval from t = 1 s to t = 4 s.
Solution
Differentiating s = 2t3 – 24t + 6 à v = 6t2 – 24 m/s
à a = 12t m/s2
(a) v = 72 m/s à t = ± 4 s
(- 4 s happened before initiation of motion à no physical interest.)
à t = 4 s
(b) v = 30 m/s à t = 3 sec à a = 36 m/s2
(c) t = 1 s to 4 s. Using s = 2t3 – 24t + 6
Δs = s4 – s1 = [2(43) – 24(4) +6] – [2(13) – 24(1) + 6]
Δs = 54 m

14. Working example-1
The position coordinate of a particle which is confined to move along a straight line is given
by s = 2t3-24t+6, where s is measured in meters from a convenient origin and t is in seconds.
Determine;
(a) the time required for the particle to reach a velocity of 72 m/s from its initial condition at
t=0.
(b) the acceleration of the particle when 𝑣=30 m/s.
(c) the net displacement of the particle during the interval from t =1 s to t=4 s.

15. Working example-1
The position coordinate of a particle which is confined to move along a straight
line is given by s = 2t3-24t+6, where s is measured in meters from a convenient
origin and t is in seconds. Determine;
(a) the time required for the particle to reach a velocity of 72 m/s from its initial
condition at t=0.
Given;
s = 2t3+24t+6
to=0 , 𝑣𝑓 = 72m/s
RTC;
Time tf when 𝑣𝑓=72m/s
Solution (a)
From; eq.1
𝑣 =
)*
)+
= 𝑆̇,
𝑣𝑓 =
)(2t3+24t+6)
)+
𝑣𝑓 = 6t2+24
Therefore; t = 4
2
3 𝑠

16. Working example-1
The position coordinate of a particle which is confined to move along a straight
line is given by s = 2t3-24t+6, where s is measured in meters from a convenient
origin and t is in seconds. Determine;
(b) the acceleration of the particle when 𝑣=30 m/s.
Given;
s = 2t3+24t+6
to=0 , 𝑣𝑓 = 30m/s
RTC; 𝒂 at 𝑣𝑓 Solution (b)
From; eq.2
𝑎 =
)9
)+
= 𝑣̇,
𝑎 =
)(6t2+24)
)+
𝒂 = 12t
from; 𝑣𝑓 = 6t2+24
t = 3
2
3
𝑠 , 3s
Therefore
a=12x3=36 m/s2

17. Working example-1
The position coordinate of a particle which is confined to move along a straight line
is given by s = 2t3-24t+6, where s is measured in meters from a convenient origin
and t is in seconds. Determine;
(c) the net displacement of the particle during the interval from t =1 s to t=4 s.
Given;
s = 2t 3+24t+6
RTC; ∆𝑆 between t=1s to t=4s
Solution;
Net displacement S= S (4)-S(1)
Where; S(1)=2(1)3-24(1)+6 = -16m
S(2)= 2(4)3-24(4)+6 = 38m
Therefore;
S= 54m

18. Working example-2
A particle moves along the x-axis with an initial velocity vx=50 ft/sec at the origin
when t=0. For the first 4 seconds it has no acceleration, and thereafter it is acted
on by a retarding force which gives it a constant acceleration ax= -10 ft/sec2.
Calculate the velocity and the x-coordinate of the particle for the conditions of t=8
sec and t=12 sec and find the maximum positive x-coordinate reached by the
particle.
At t=8 sec and t=12 sec, the velocities along x axis are;

19. Working example-2
A particle moves along the x-axis with an initial velocity vx=50 ft/sec at the origin
when t=0. For the first 4 seconds it has no acceleration, and thereafter it is acted
on by a retarding force which gives it a constant acceleration ax=-10 ft/sec2.
Calculate the velocity and the x-coordinate of the particle for the conditions of t=8
sec and t=12 sec and find the maximum positive x-coordinate reached by the
particle.
Solution continue;
The distance travelled by the particle (x-coordinate) after 4 sec, is obtained by
adding the distance covered in 4 sec and that after change of acceleration; hence
from eq. 1;

20. Working example-2
A particle moves along the x-axis with an initial velocity vx=50 ft/sec at the origin when
t=0. For the first 4 seconds it has no acceleration, and thereafter it is acted on by a
retarding force which gives it a constant acceleration ax=-10 ft/sec2. Calculate the
velocity and the x-coordinate of the particle for the conditions of t=8 sec and t=12 sec
and find the maximum positive x-coordinate reached by the particle.
Solution continue;
It was noted the x coordinate when t=8 sec was greater than that of t=12sec. That is
because the motion is in negative during t=12 sec. Hence the max x-coordinate is
reached when the 𝑣x = 0. (t=9sec). Therefore;

21. Working example-3
Solution;
Since the acceleration is given in term of displacement,
then from from eqn. 3.

22. Working example-3
From eg.1, substitute the value of 𝑣;