Dokumen tersebut memberikan penjelasan tentang vektor, termasuk pengertian skalar dan vektor, operasi aljabar vektor seperti perkalian skalar dengan vektor, penjumlahan vektor, dan panjang vektor. Juga dijelaskan beberapa contoh soal untuk memahami konsep-konsep tersebut.









![1. Koordinat titik P(4,-3) dan Q(-1,9). Hitunglah :
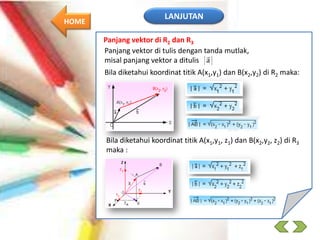
• Panjang vektor p
• Panjang vektor q
• Panjang vektor PQ dan vektor satuan PQ
2. Tentukan nilai k, agar vektor a = [3,k-1] mempunyai
panjang sama dengan 5
3. Koodinat titik A(x,-6) dan B(1,x). Tentukan nilai x agar
panjang vektor AB = 13
4. Tentukan nilai k agar vektor a = [3,k,1] mempunyai
panjang
5. Vektor a = [4,x,-1] dan vektor b = [2,-3,6]. Tentukan nilai
x, jika panjang vektor a sama dengan panjang vektor b
6. Diketahui vektor p = [5,2,8] dan vektor q = [2,5,-4]
Hitunglah :
•
•
26
qpdanqp
qpdanqp
EVALUASIHOME](https://image.slidesharecdn.com/kelasxiikd3-130805033915-phpapp01/85/Bahan-Ajar-Vektor-Kelas-XII-13-320.jpg)

