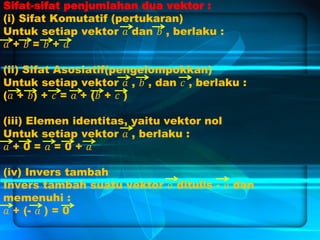
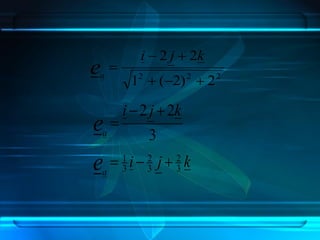Dokumen ini membahas tentang vektor dan operasinya, termasuk pengertian besaran vektor dan skalar serta notasi penulisan vektor. Ini juga menjelaskan cara menggambarkan vektor, operasi penjumlahan, pengurangan, dan sifat-sifat vektor. Selain itu, terdapat contoh soal dan penerapan konsep vektor dalam geometri.

1. Assalamualaikum Wr.Wb.
Anggota :
Dalilah Sakinah P
Fanny Anggraini
Hamalna Putri Elsyipa
Nyimas Intan Kemuning
Rima Marliza
Ahmad Huzayfi
Muhammad Ibrahim
M.Ramadhan Zulkarnain
X.IPA 1
Kelompok 1
Guru Pembimbing : Nurbahari Martlan,S.Pd.

2. Pengertian Dasar Vektor dan Operasinya
1.Notasi Vektor dan Beberapa Jenis Vektor
A.Besaran Skalar dan Besaran Vektor
Besaran skalar atau disebut skalar adalah suatu
besaran yang hanya mempunyai besar saja, seperti: panjang,
waktu, massa, suhu/temperatur.
Luas dan isi atau volume merupakan besaran skalar.
Setiap besaran skalar biasanya dinyatakan oleh sebuah
bilangan.
Besaran vektor atau disebut vektor adalah sebuah
besaran yang mempunyai besar dan arah, seperti; kecepatan,
percepatan, gaya, momentum, dan medan magnet. Secara
geometris, vektor adalah suatu ruas garis berarah.

3. Contoh:
Vektor:
1. Kecepatan
2. Gaya
3. Perpindahan
4. Percepatan
Skalar:
1. Tinggi Badan
2. Jumlah Siswa
dalam kelas
3. Panjang sebuah
meja
4. Volume bangun
Ruang

4. Notasi Penulisan Vektor
 Bentuk vektor kolom:







4
3
u











0
2
1
PQatau
 Bentuk vektor baris:
 4,3AB  atau  0,3,2v 
 Vektor ditulis dengan notasi:
i, j dan k
misal : a = 3i – 2j + 7k

5. B.Menggambar dan Menulis Sebuah Vektor
Sebuah vektor digambarkan dengan sebuah anak
panah (→) yang terdiri atas pangkal, panjang dan arah
anak panah. Perhatikan gambar contoh vektor berikut
ini:
Pada gambar anak panah di atas, pangkal anah
panah menunjukkan titik tangkap (titik awal) sebuah
vektor, panjang anak panah mewakili besar atau nilai
vektor (semakin panjang anak panah maka semakin besar
nilai atau harga vektor dan sebaliknya), sedangkan arah
anak panah menunjukkan arah vektor.

6. Untuk lebih jelas mengenai cara menggambarkan vektor,
perhatikan contoh gambar vektor di bawah ini.
Gambar (a) menunjukkan vektor gaya F sebesar 5 N ke arah kana
Gambar (b) menunjukkan vektor gaya F sebesar 10 N ke arah kiri
Penulisan simbol atau lambang vektor dapat
dilakukan dengan 2 cara sebagai berikut:
1. Vektor disimbolkan dengan dua huruf besar atau
satu huruf yang di atasnya diberi tanda anak panah.

7. 2.Vektor disimbolkan dengan dua huruf besar atau satu huruf
yang ditebalkan
Jika kalian menggunakan dua huruf, maka huruf pertama
(A) merupakan titik asal vektor, atau juga disebut pangkal
vektor. Sementara huruf di belakang (B) merupakan arah vektor
atau titik terminal atau ujung vektor.

8. A
B
ditulis vektor AB atau u
Adisebut titik pangkal
B disebut titik ujung
u
45 X
Gambar Vektor :

9. C.Besar atau Panjang Sebuah Vektor
Besar atau Panjang Vektor ditulis dengan IaI atau lbl,
sedangkan besar vektor AB ditulis sebagai lABl atau lABl.
D.Vektor nol
Sebuah Vektor yang titik awal dan titik ujungnya sama
(berimpit) disebut vektor nol, seperti: AA= O, BB = O. Vektor
nol mempunyai panjang nol dan arah tak tentu.
E.Vektor Satuan
Vektor satuan adalah vektor yang panjangnya satu
satuan
a
a
e 

ˆ

10. Contoh: Vektor Satuan dari
vektor a = i - 2j+ 2k
adalah….
Jawab:
a
a
ea

222
2)2(1
22



kji
ea

11. 222
2)2(1
22



kji
ea
3
22 kji
ea


kjiea 3
2
3
2
3
1


12. 2. Operasi Vektor
Operasi vektor meliputi perkalian sebuah vektor dengan
sebuah skalar, penjumlahan dua vektor, selisih dua vektor,
vektor posisi, teorema titik tengah , dan resultan dari beberapa
vektor.
A. Perkalian sebuah vektor dengan skalar
Jika k suatu bilangan real dan 𝑎 suatu vektor, perkalian k
𝑎 menghasilkan suatu vektor yang panjangnya 𝑘 kali panjang
vektor 𝑎 dan arahnya sama dengan arah 𝑎 jika k >0, atau
berlawanan dengan 𝑎 jika k < 0. jika k = 0, maka diperoleh
vektor nol.
Sifat-sifat perkalian vektor dengan skalar
(i) k(- 𝑎 ) = -(k 𝑎 ) = -k 𝑎 (iii) (k ± m) 𝑎 = k 𝑎 ± m 𝑎
(ii) K(m 𝑎 ) = (km) 𝑎 = m(k 𝑎 ) (iv) k( 𝑎 ± 𝑏 = k 𝑎 ± k 𝑏

13. B.Penjumlahan dua Vektor
Jumlah dua vektor atau lebih disebut vektor hasil atau
resultan. Untuk menjumlahkan dua buah
vektor 𝑎 dan 𝑏 , dapat kita gunakan 2 metode sebagai berikut.
1. Metode Segitiga
Vektor hasil ( resultan ), yaitu 𝑎 + 𝑏 , diperoleh dengan
menempatkan titik awal salah satu vektor (misalnya 𝑏 ) pada
titik ujung vektor yang lainnya. Resultan dari 𝑎 + 𝑏 dengan
metode segitiga merupakan vektor yang bertitik awal di titik
awal 𝑎 dan bertitik ujung 𝑏 . Apabila 𝐴𝐵 = 𝑎 dan 𝐵𝐶 = 𝑏 , maka AC
= 𝑎 + 𝑏 . Sehingga diperoleh :
𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶
2. Metode Jajargenjang
Resultan 𝑎 dan 𝑏 diperoleh dari diagonal jajargenjang
yang dibentuk oleh 𝑎 dan 𝑏 setelah titik awal 𝑎 dan 𝑏
ditempatkan berimpit.

14. 3. Resultan dari beberapa vektor
Untuk menentukan resultan dari beberapa vektor.
Berarti kita menentukan penjumlahan lebih dari
dua vektor sehingga dapat digunakan cara poligon.cara ini
merupakan pengembangan metode segitiga.
Perhatikan :
Δ ABC, didapat 𝐴𝐵 + 𝐵𝐶 = 𝐴𝐶
Δ ACD, didapat 𝐴𝐶 + 𝐶𝐷 = 𝐴𝐷
Δ ADE, didapat 𝐴𝐷 + 𝐷𝐸 = 𝐴𝐸
Hal ini berarti :
𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷 + 𝐷𝐸 = 𝐴𝐸

15. Sifat-sifat penjumlahan dua vektor :
(i) Sifat Komutatif (pertukaran)
Untuk setiap vektor 𝑎 dan 𝑏 , berlaku :
𝑎 + 𝑏 = 𝑏 + 𝑎
(ii) Sifat Asosiatif(pengelompokkan)
Untuk setiap vektor 𝑎 , 𝑏 , dan 𝑐 , berlaku :
(𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐 )
(iii) Elemen identitas, yaitu vektor nol
Untuk setiap vektor 𝑎 , berlaku :
𝑎 + 0 = 𝑎 = 0 + 𝑎
(iv) Invers tambah
Invers tambah suatu vektor 𝑎 ditulis - 𝑎 dan
memenuhi :
𝑎 + (- 𝑎 ) = 0

16. C. Selisih dua vektor
Jika 𝑏 + 𝑥 = 𝑎 , maka 𝑥 dapat ditulis sebagai 𝑎 +
(-𝑏 ) atau ditulis sebagai 𝑥 = 𝑎 - 𝑏 .
𝐴𝐵 - 𝐴𝐶 = 𝐶𝐵 atau 𝐴𝐵 + 𝐶𝐴 = 𝐶𝐵
D. Vektor posisi
Vektor posisi dari titik A terhadap pusat O ditulis 𝑂𝐴 atau
𝑎 . Gambar tersebut menunjukkan posisi dari titik A, B, dan C
terhadap pusat O ditulis 𝑂𝐴 , 𝑂𝐵 , dan 𝑂𝐶 . Vektor 𝑂𝐴 , 𝑂𝐵 , dan 𝑂𝐶
disebut vektor posisi dari titik A, B dan C. Vektor posisi dari
titik A, B, dan C sering ditulis dengan huruf kecil 𝑎 , 𝑏 , dan 𝑐 .
perhatikan Δ ABO di samping, terlihat bahwa :
𝐴𝐵 = 𝐴𝑂 + 𝑂𝐵
= -𝑂𝐴 + 𝑂𝐵
= 𝑂𝐵 - 𝑂𝐴
∴ 𝐴𝐵 = 𝑏 - 𝑎

17. E. Teorema titik tengah
Jika titik A dan B mempunyai vektor posisi 𝑎 dan 𝑏
terhadap O, maka vektor posisi dari titik M yang merupakan
titik tengah dari titik A dan B, ditulis vektor posisi 𝑚 ,yaitu :
𝐴𝐵 = 𝑏 - 𝑎
𝐴𝑀 = 𝑀𝐵 , berarti 𝐴𝑀 = ½(𝐴𝐵 )
𝐴𝑀 = ½(𝑏 - 𝑎 )
Pandang, 𝑂𝑀 = 𝑂𝐴 + 𝐴𝑀
= 𝑎 + ½(𝑏 - 𝑎 )
𝑂𝑀 = ½(𝑎 + 𝑏 )
∴ 𝑚 = ½(𝑎 + 𝑏 )

18. Contoh Soal :
Diketahui titik-titik P(-1,3,0)
dan Q(1,2,-2).
Tentukan panjang vektor PQ
(atau jarak P ke Q) !

19. Jawab: P(1,2,-2)
Q(-1,3,0)
PQ = q – p =































2
1
2
2-
2
1
-
0
3
1-












2
2
1
p











0
3
1
q

20. 










2
1
2
PQ
222
21)2(PQ 
39PQJadi 

21. Tafsiran Geometri dari Kedudukan Dua
Vektor atau Lebih
Perluasan vektor posisi
Pengertian vektor posisi yaitu vektor dengan pangkal O
dan berujung disembarang titik bukan O, misalkan sebuah titik
pangkal O dikaitkan dengan sembarang titik P , berarti 𝑂
disebut vektor posisi dari titik P terhadap O. Vektor 𝑂𝑃 sering
ditulis sebagai 𝑝 . Sembarang vektor 𝑃𝑄 dapat dituliskan dalam
vektor posisi 𝑝 dan 𝑞 , yaitu :
A. Vektor Posisi dari Titik Formula Pembagian
Suatu titik C membagi ruas garis AB dala perbandingan m dan n
sehingga AC : BC = m : n
Jika C di dalam AB, maka AC→AC→, CB→CB→ mempunyai arah
yang sama dan m, n mempunyai tanda yang sama.
AC : CB = m : n
AC : AB = m : (m + n)
∴ 𝑝 =n𝑎 + m𝑏
m + n

22. Contoh Soal :
Diberikan vektor posisi dari titik P,Q,dan R terhadap titik
O : p= 9a – 4b, q = -3a – b, dan r = 5a – 3b.
A. Nyatakanlah setiap vektor dibawah ini dalam a dan b .
(i) PQ (ii) QR
B. Apakah PQ dan QR sejajar ? Bagaimana arah PQ dan QR ?
Pembahasan :
A. (i) PQ = q – p
= -3a – b – (9a – 4b)
= -3a – b - 9a + 4b
PQ = -12a + 3b = -3(4a – b)
(ii) QR = r – q
= 5a – 3b – (-3a – b)
= 5a – 3b + 3a + b
QR = 8a – 2b = 2(4a – b)
B. Dari Jawaban terlihat bahwa: PQ = -3/2QR, berarti PQ dan QR sejajar dalam
arah berlawanan

23. Terima Kasih
Dari Kelompok : 1 (Satu)
Wassalamualaikum Wr.Wb