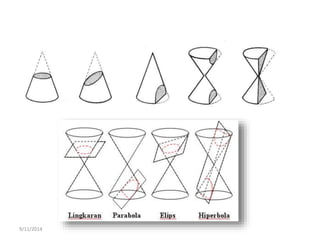
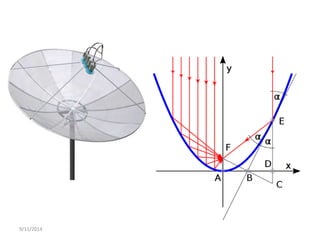
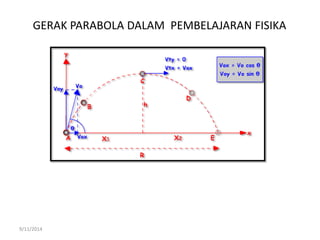
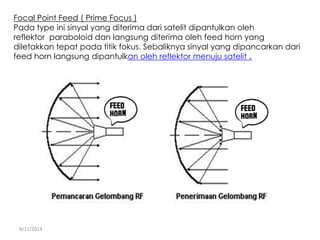
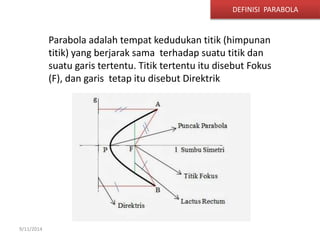
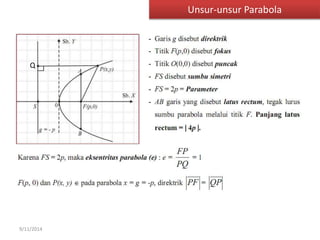
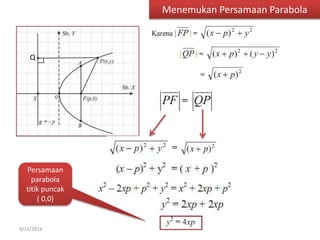
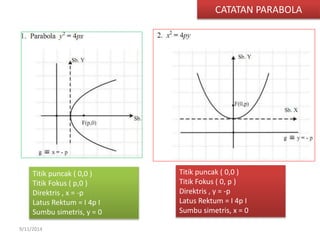
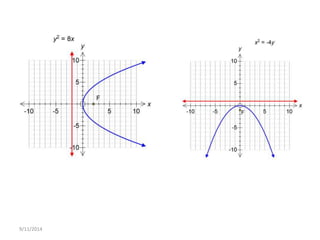
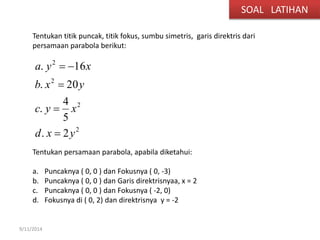
Dokumen tersebut membahas tentang gerak parabola dalam pembelajaran fisika dan olahraga ekstrem. Terdapat penjelasan mengenai definisi parabola, unsur-unsur parabola, persamaan parabola, contoh soal dan latihan mengenai penentuan titik puncak, titik fokus, sumbu simetris dan garis direktris dari persamaan-persamaan parabola.

1. MAHMUD YUNUS
www.mahmudsmk5.wordpress.com
9/11/2014

2. 9/11/2014

3. 9/11/2014

4. 9/11/2014

5. GERAK PARABOLA DALAM PEMBELAJARAN FISIKA
9/11/2014

6. Focal Point Feed ( Prime Focus )
Pada type ini sinyal yang diterima dari satelit dipantulkan oleh
reflektor paraboloid dan langsung diterima oleh feed horn yang
diletakkan tepat pada titik fokus. Sebaliknya sinyal yang dipancarkan dari
feed horn langsung dipantulkan oleh reflektor menuju satelit .
9/11/2014

7. 9/11/2014
GERAK PARABOLA DALAM
OLAHRAGA EKSTREM

8. 9/11/2014
DEFINISI PARABOLA
Parabola adalah tempat kedudukan titik (himpunan
titik) yang berjarak sama terhadap suatu titik dan
suatu garis tertentu. Titik tertentu itu disebut Fokus
(F), dan garis tetap itu disebut Direktrik

9. 9/11/2014
MENGINGAT KEMBALI

10. Q
9/11/2014
Unsur-unsur Parabola

11. Q
Persamaan
parabola
titik puncak
( 0,0)
9/11/2014
Menemukan Persamaan Parabola

12. PARABOLA
MEMBUKA KE
9/11/2014
Temukan Sendiri Persamaannya?
P
Q
PF  PQ
x   y  p  p  y 2 2 ( 0) ( )
Masing-masing ruas di kuadratkan
2 2 2 (x  0)  ( y  p)  ( p  y)
Di jabarkan
2 2 2 2 2 x  y  2 py  p  p  2 py  y
x 2 py 2 py 2  
x 4 py 2 
ATAS
Persamaan
parabola
titik puncak
( 0,0)

13. 9/11/2014
CATATAN PARABOLA

14. 9/11/2014
CATATAN PARABOLA
Titik puncak ( 0,0 )
Titik Fokus ( p,0 )
Direktris , x = -p
Latus Rektum = I 4p I
Sumbu simetris, y = 0
Titik puncak ( 0,0 )
Titik Fokus ( 0, p )
Direktris , y = -p
Latus Rektum = I 4p I
Sumbu simetris, x = 0

15. 2
a . y 8
x
. 4
9/11/2014
CONTOH SOAL
Tentukan titik puncak, titik fokus, sumbu simetris, garis direktris dari
persamaan parabola berikut:
2

b x  
y
a. Penyelesaian
4p = 8
p = 2
Puncak ( 0, 0)
Fokus ( 2, 0)
Direktris, x = -2
Sumbu simetris, y= 0
b. Penyelesaian
4p =-4
p = -1
Puncak ( 0, 0)
Fokus ( 0, -1)
Direktris, y = 1
Sumbu simetris, x= 0

16. 9/11/2014

17. a . y  
16
x
b . x 
20
y
c .
y 
x
d x y
9/11/2014
SOAL LATIHAN
Tentukan titik puncak, titik fokus, sumbu simetris, garis direktris dari
persamaan parabola berikut:
2
2
2
2
4
5
. 
2
Tentukan persamaan parabola, apabila diketahui:
a. Puncaknya ( 0, 0 ) dan Fokusnya ( 0, -3)
b. Puncaknya ( 0, 0 ) dan Garis direktrisnyaa, x = 2
c. Puncaknya ( 0, 0 ) dan Fokusnya ( -2, 0)
d. Fokusnya di ( 0, 2) dan direktrisnya y = -2

18. 9/11/2014
THANK YOU