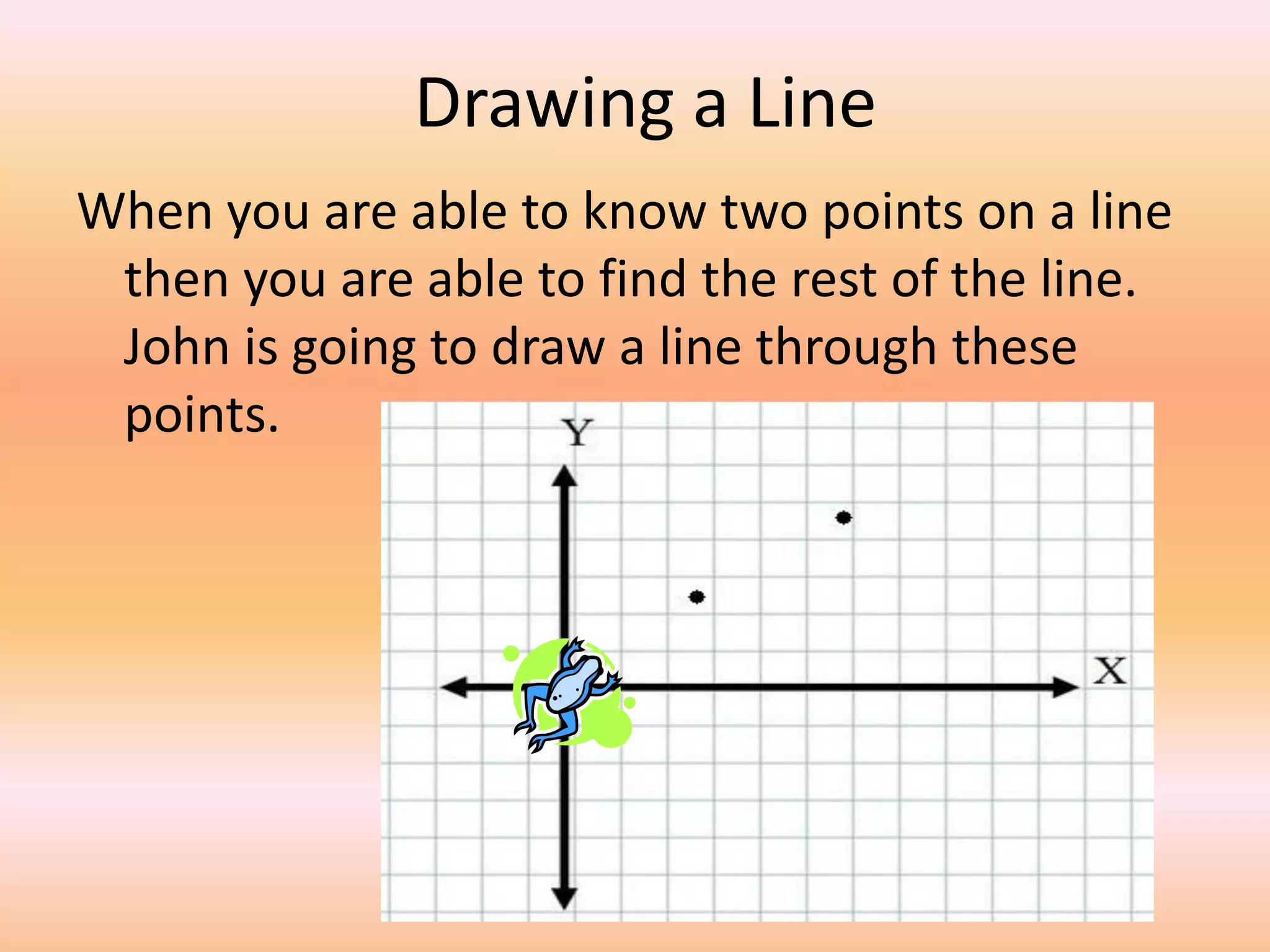
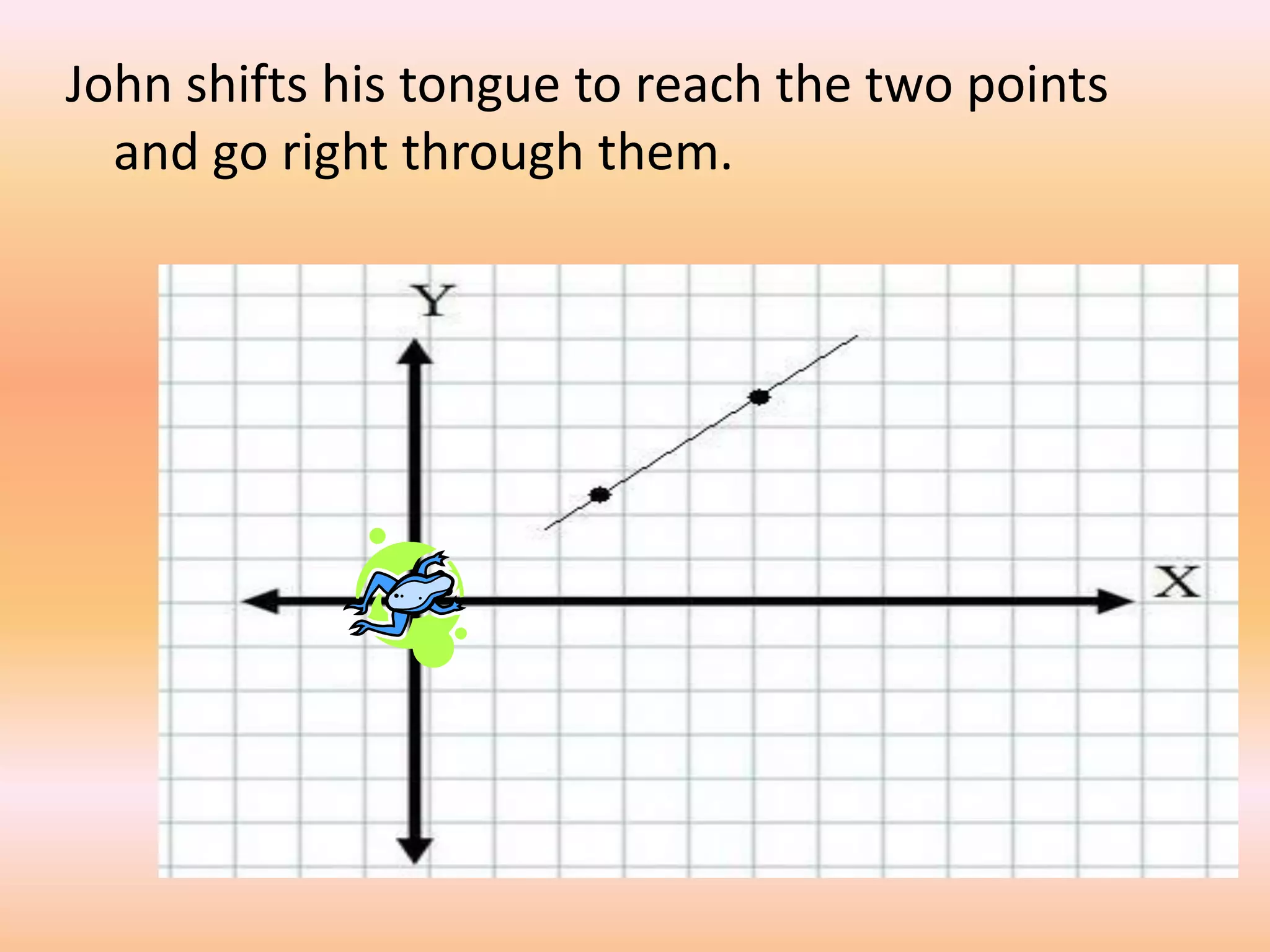
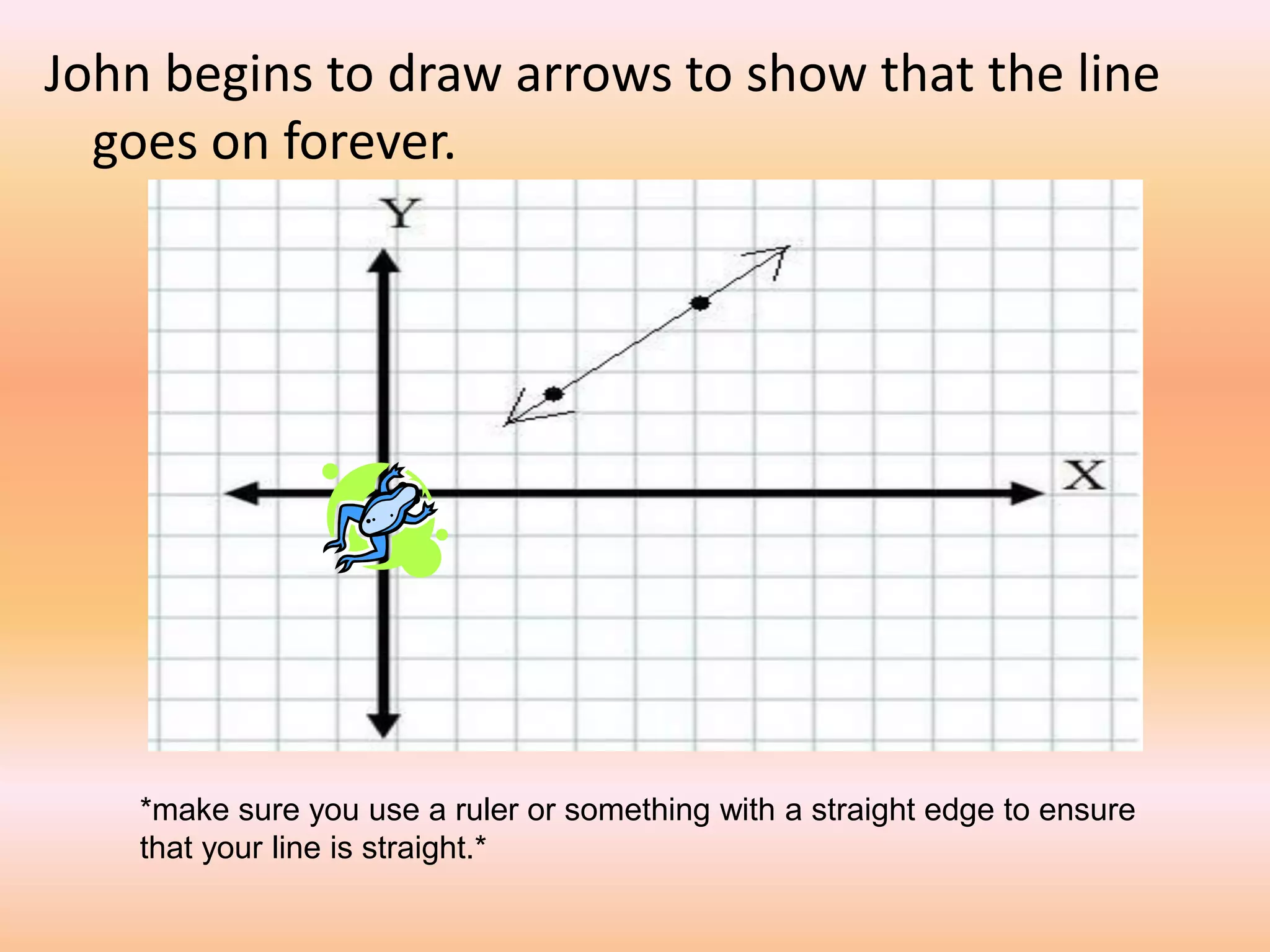
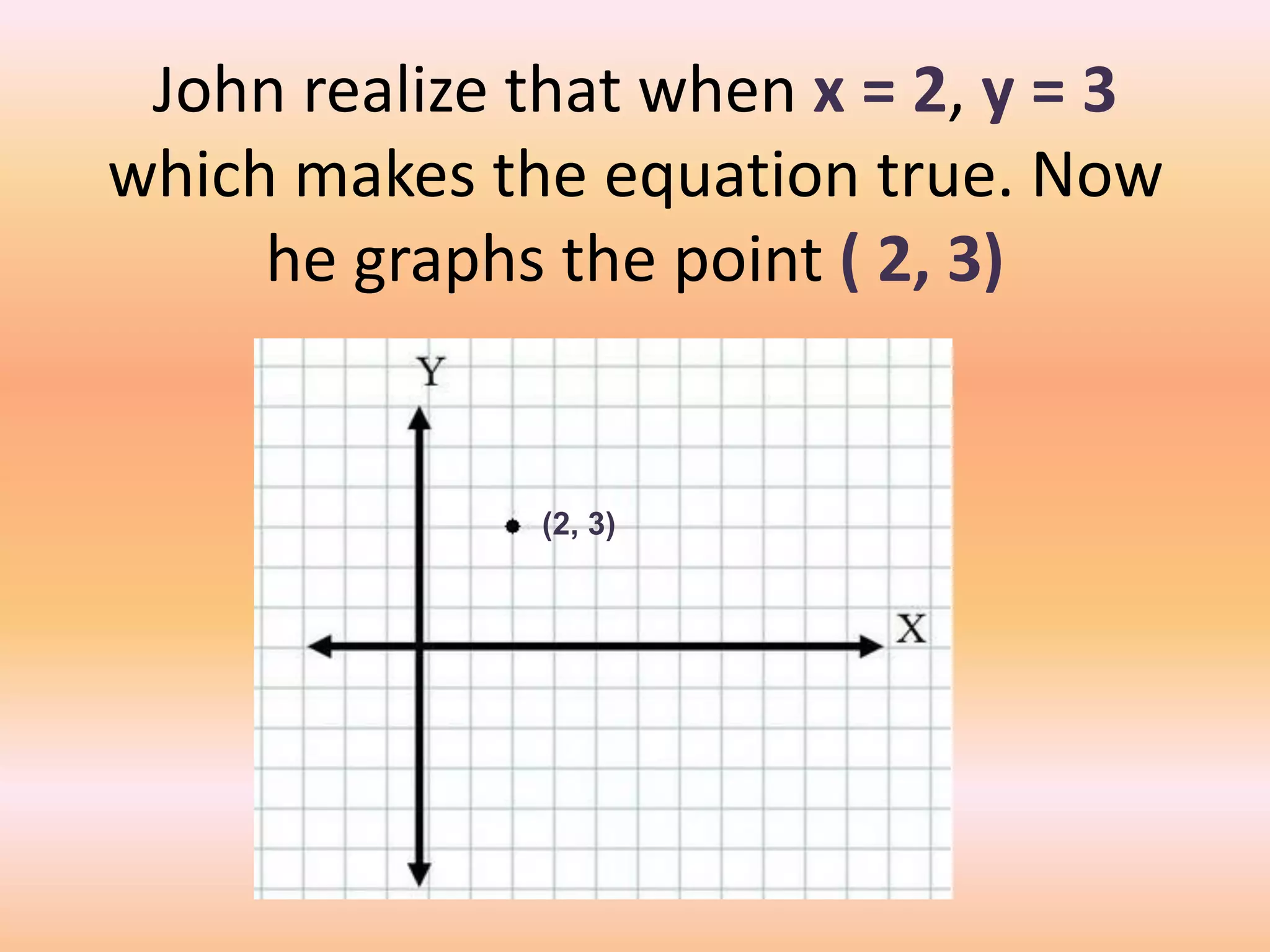
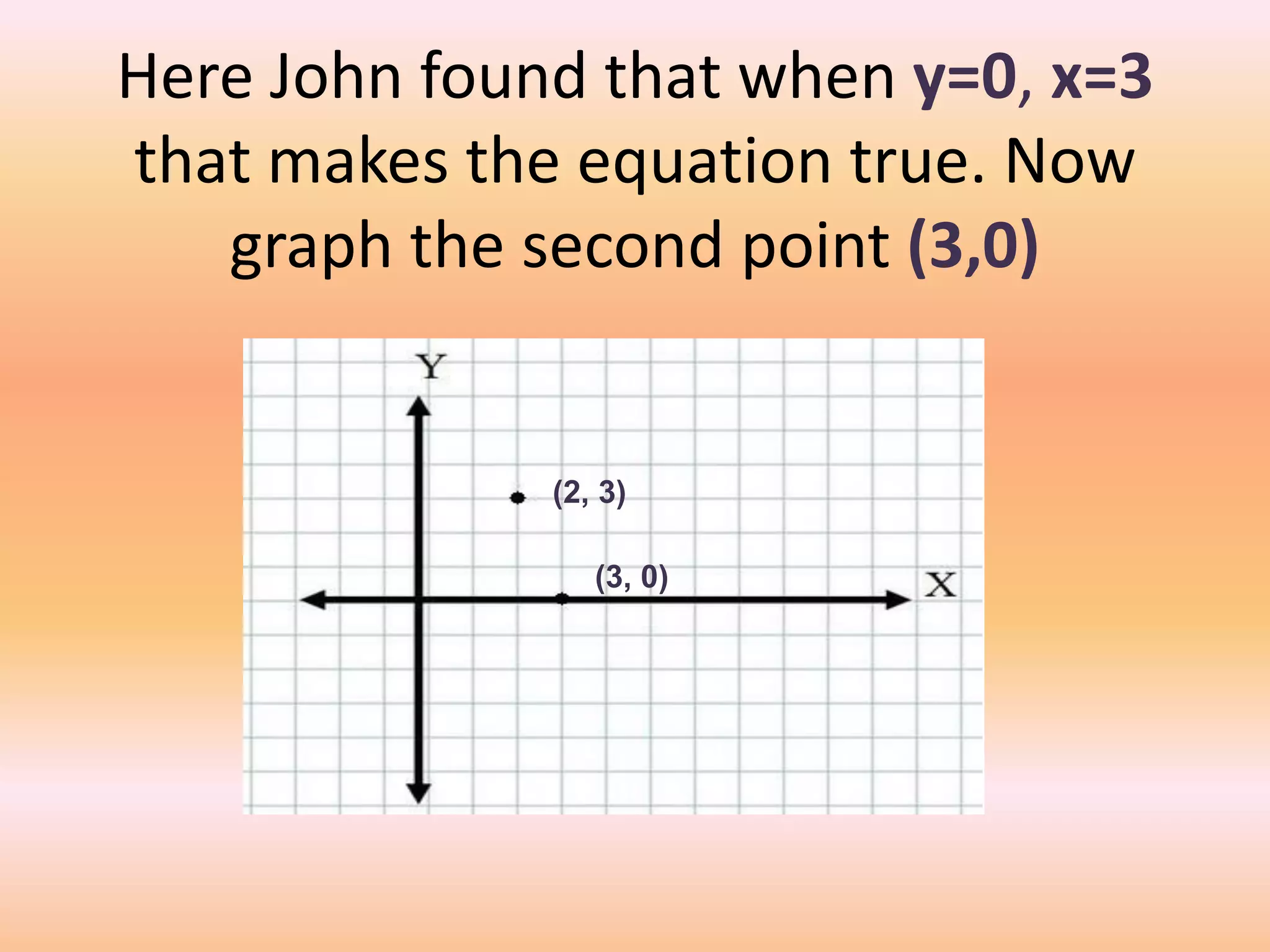
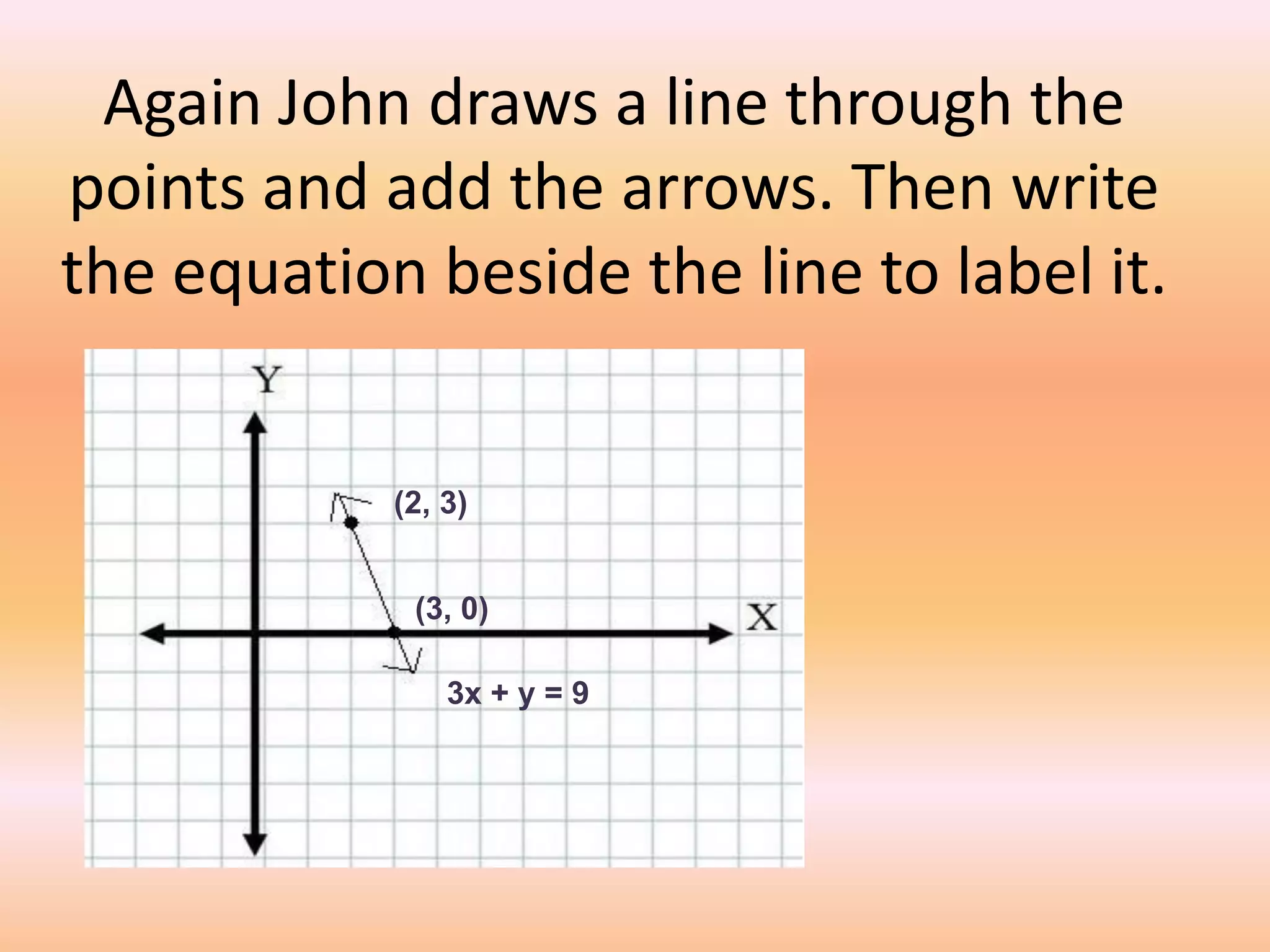
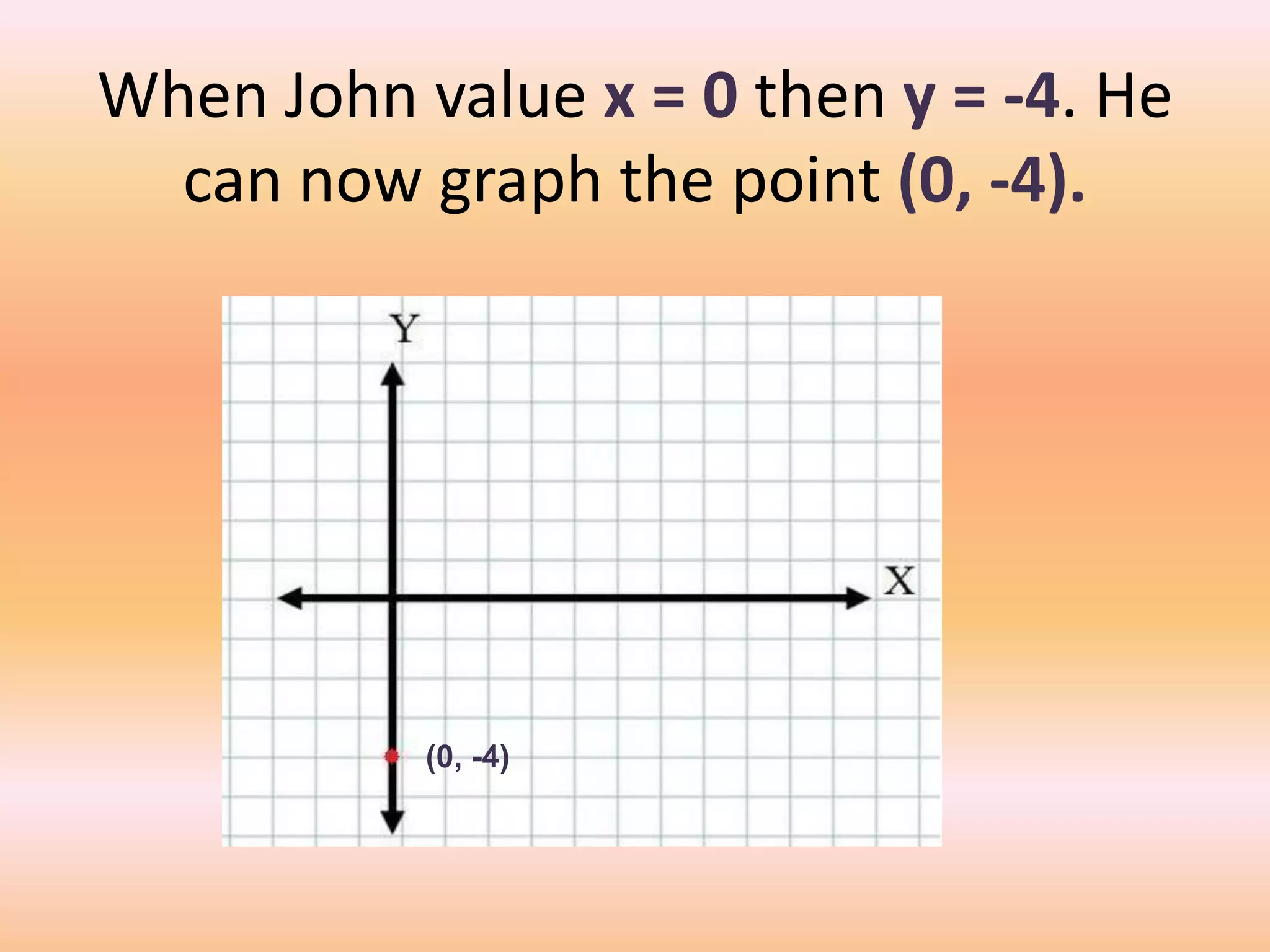
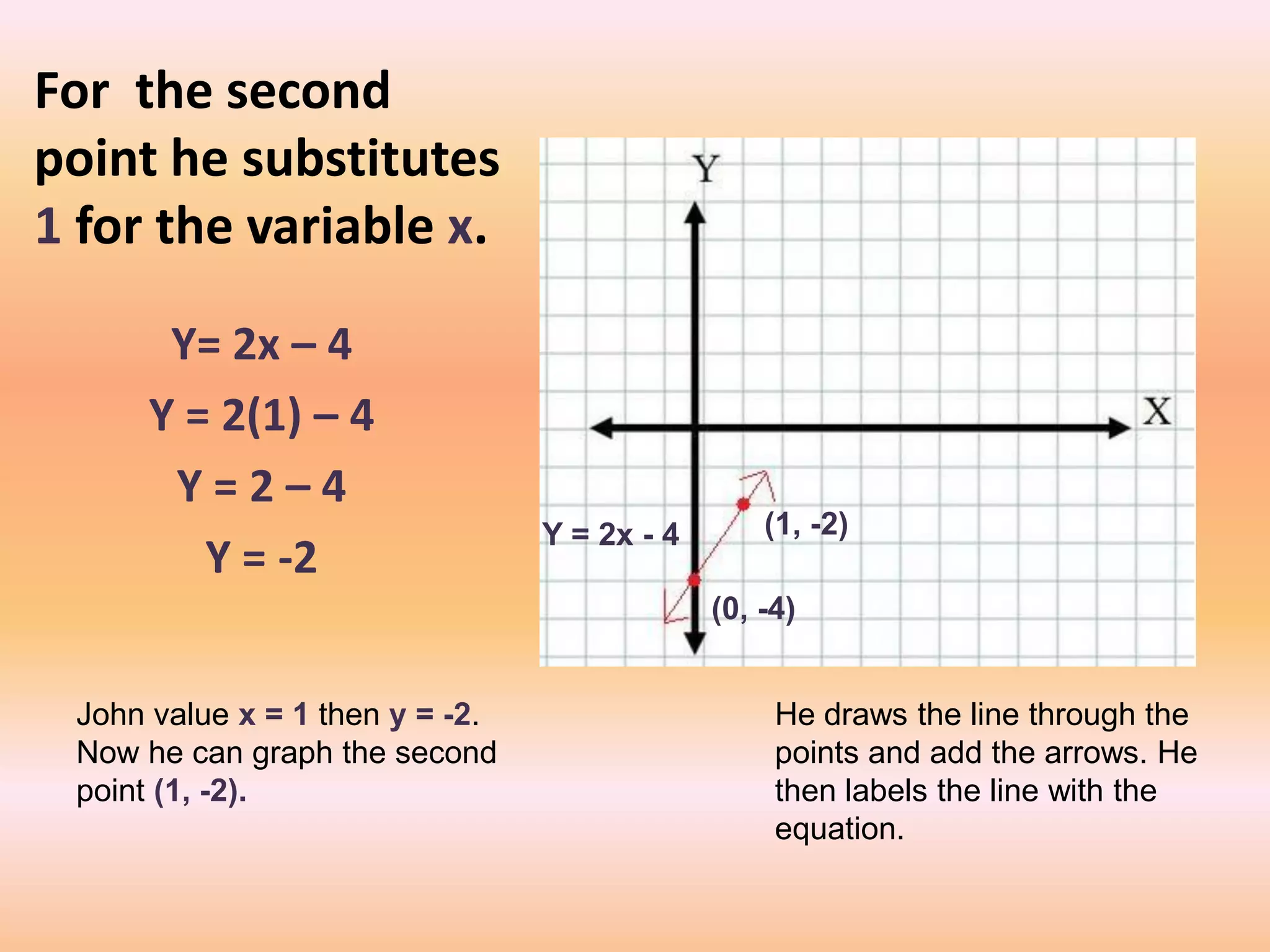
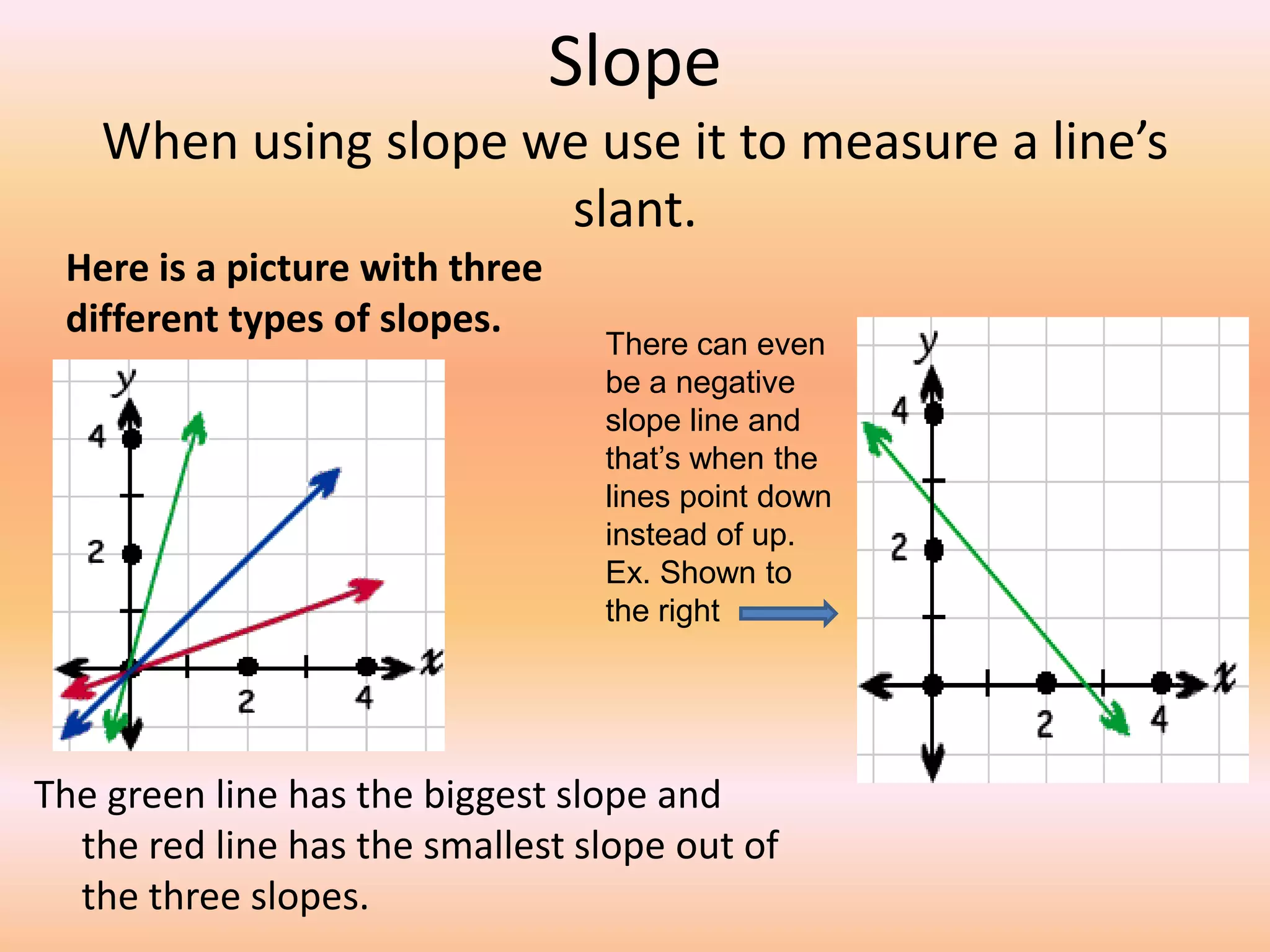
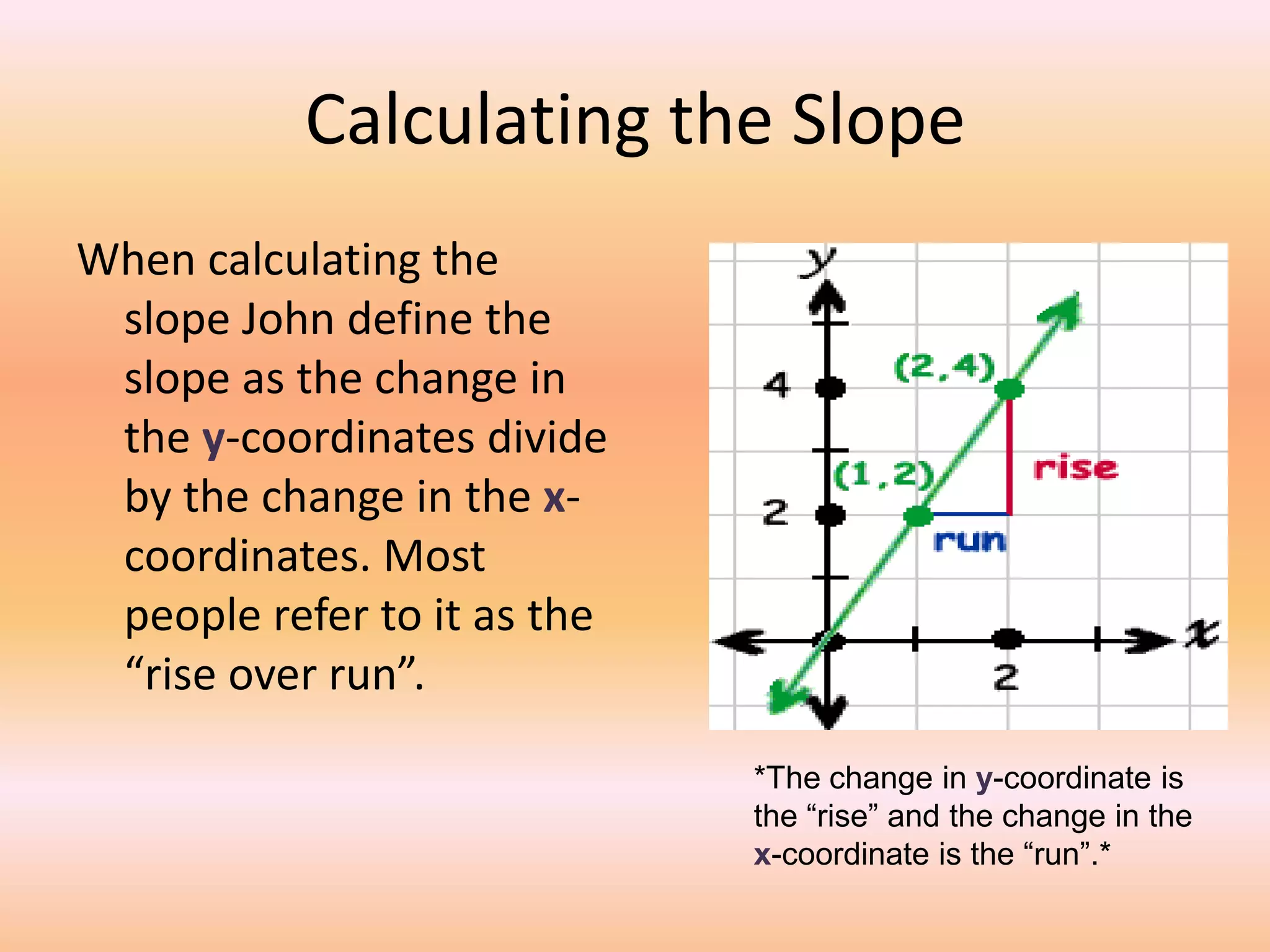
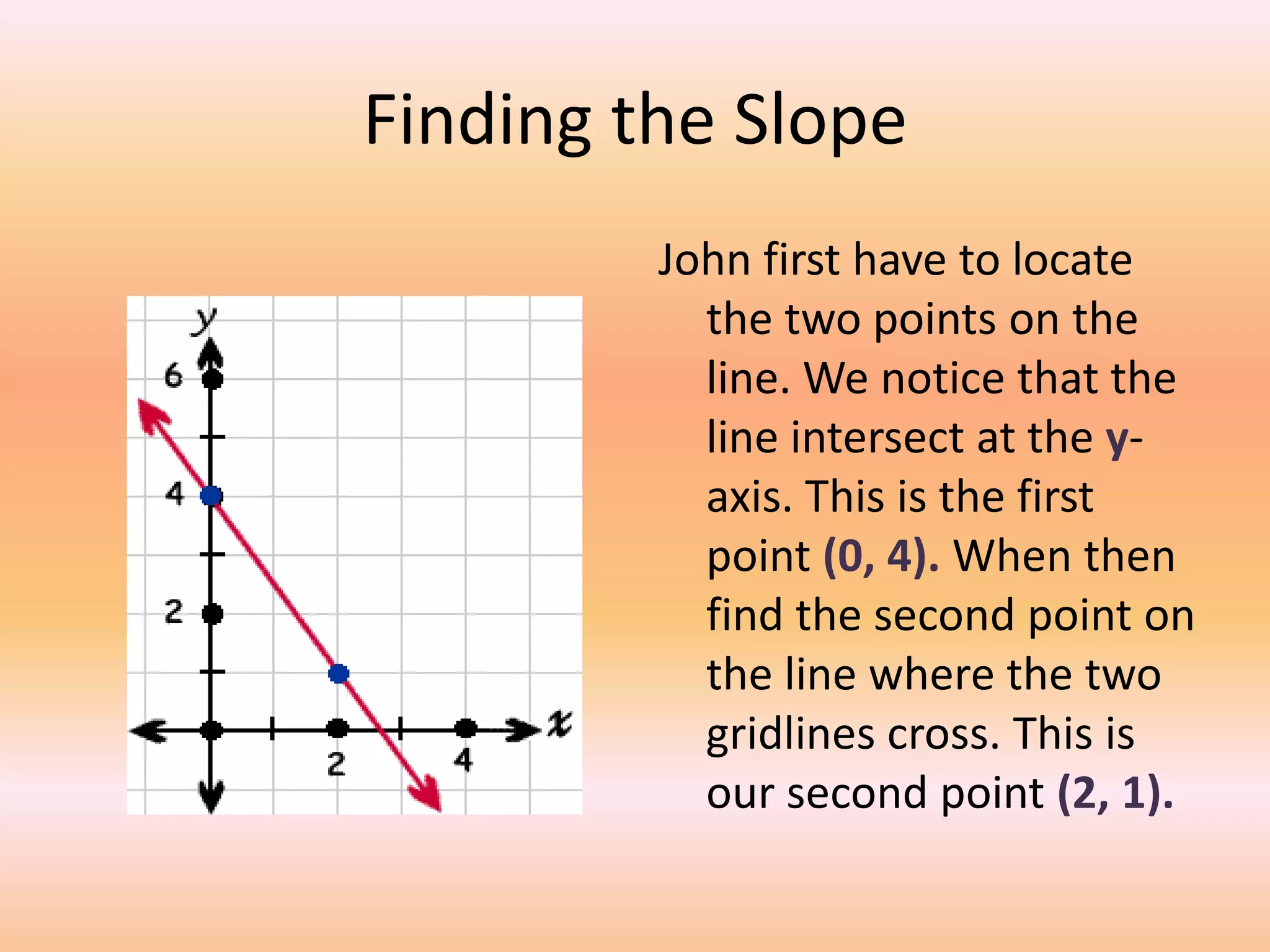
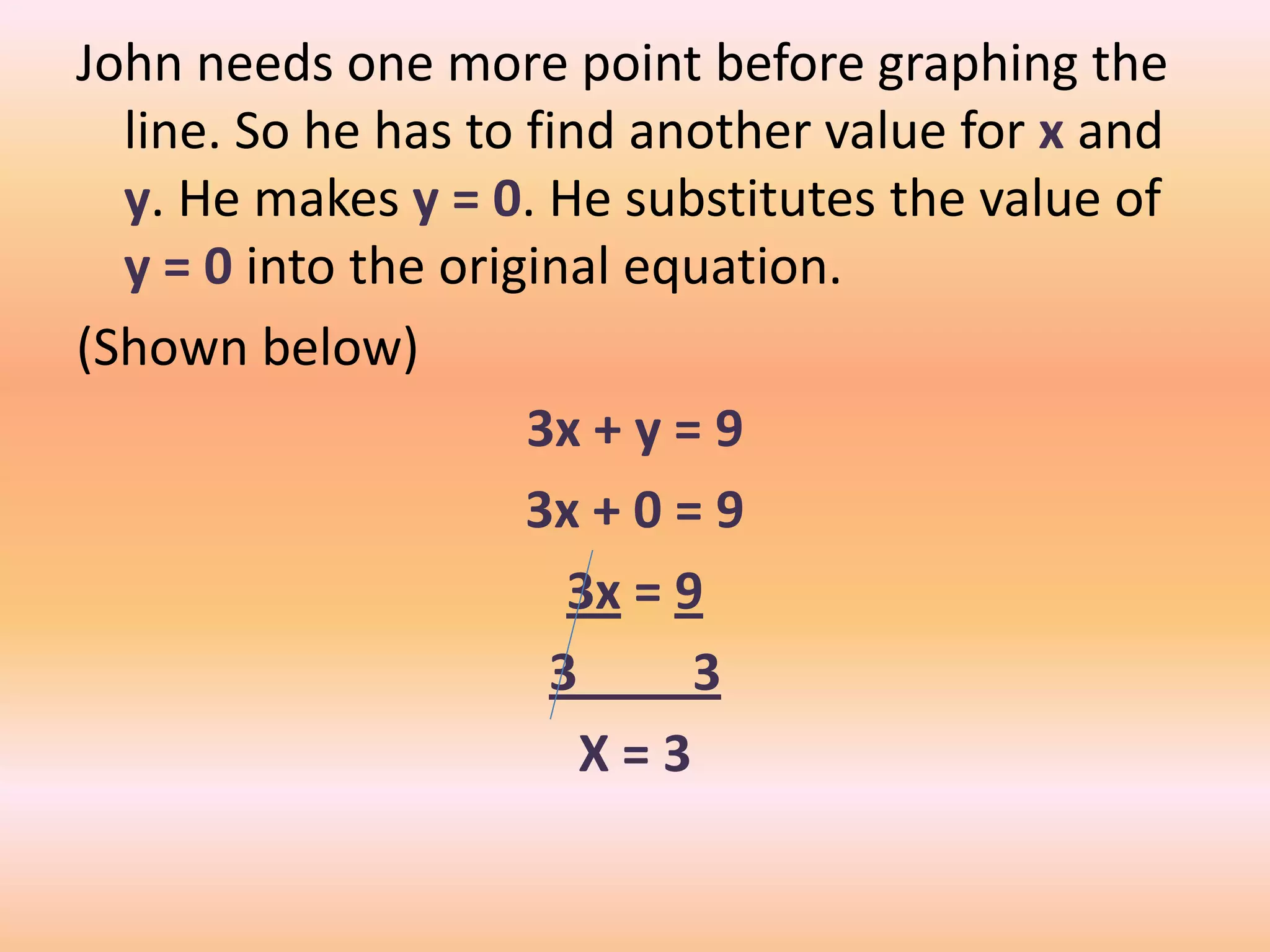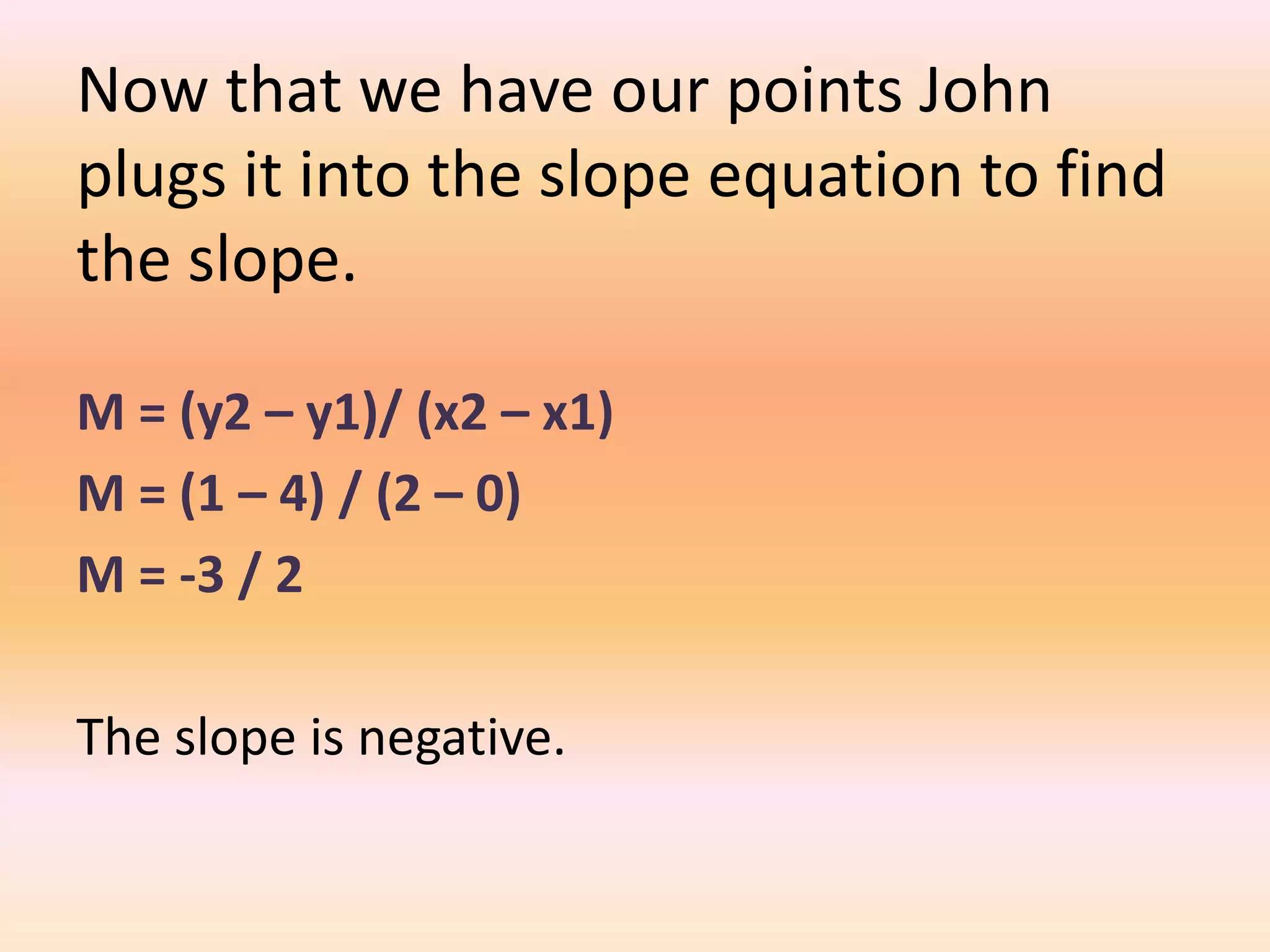This document provides a lesson on lines and slopes. It discusses drawing a line by graphing points, calculating slope using the formula of rise over run, and finding slopes of different lines. John uses his knowledge of lines and slopes to help catch flies with his tongue. The document includes examples of graphing lines from equations and calculating the slope between two points on a line.

2. Lines and Slopes
Table of Contents
• Introduction
• Drawing a Line
- Graphing Points First
• Slope
- Calculating Slope
- Finding Those Slopes

3. Introduction
John and his friend wants to catch flies with
their tongues. Their tongues are going to go
straight just how a line would. John begins to
use his knowledge about lines to catch flies.

4. Drawing a Line
When you are able to know two points on a line
then you are able to find the rest of the line.
John is going to draw a line through these
points.

5. John shifts his tongue to reach the two points
and go right through them.

6. John begins to draw arrows to show that the line
goes on forever.
*make sure you use a ruler or something with a straight edge to ensure
that your line is straight.*

7. Graphing Points First
When graphing a line you must use an equation.
Take for example when graphing the line:
3x + y = 9 John would have to find the values x
and y to make the equation true.

8. He choices to have x value equal 2. Once John has
the value x, he has to find y by substituting the
value x=2 into the equation.
3x + y = 9
3(2) + y = 9
6+y=9
-6 =-6
Y=3

9. John realize that when x = 2, y = 3
which makes the equation true. Now
he graphs the point ( 2, 3)
(2, 3)

10. John needs one more point before graphing the
line. So he has to find another value for x and
y. He makes y = 0. He substitutes the value of
y = 0 into the original equation.
(Shown below)
3x + y = 9
3x + 0 = 9
3x = 9
3 3
X=3

11. Here John found that when y=0, x=3
that makes the equation true. Now
graph the second point (3,0)
(2, 3)
(3, 0)

12. Again John draws a line through the
points and add the arrows. Then write
the equation beside the line to label it.
(2, 3)
(3, 0)
3x + y = 9

13. To be sure John understands how to graph a
line. He graphs another equation:
y = 2x - 4
Again he has to find
two points to graph Y = 2x – 4
the equation. He has
to find the values for x Y = 2(0) – 4
and y to make sure Y=0–4
the equation is true.
For the first point he Y = -4
substitutes 0 for the
variable x.

14. When John value x = 0 then y = -4. He
can now graph the point (0, -4).
(0, -4)

15. For the second
point he substitutes
1 for the variable x.
Y= 2x – 4
Y = 2(1) – 4
Y=2–4
Y = 2x - 4 (1, -2)
Y = -2
(0, -4)
John value x = 1 then y = -2. He draws the line through the
Now he can graph the second points and add the arrows. He
point (1, -2). then labels the line with the
equation.

16. Slope
When using slope we use it to measure a line’s
slant.
Here is a picture with three
different types of slopes.
There can even
be a negative
slope line and
that’s when the
lines point down
instead of up.
Ex. Shown to
the right
The green line has the biggest slope and
the red line has the smallest slope out of
the three slopes.

17. Calculating the Slope
When calculating the
slope John define the
slope as the change in
the y-coordinates divide
by the change in the x-
coordinates. Most
people refer to it as the
“rise over run”.
*The change in y-coordinate is
the “rise” and the change in the
x-coordinate is the “run”.*

18. Slope Formula
Change in x-coordinate When identifying our
and change in my y- points, our first point
coordinate is put in a (x1, y1) and the second
formula using the Greek point (x2, y2). John
letter delta ∆. This is an substitute these points
abbreviation for in for the delta ∆.
change. Y2 –Y1
∆Y M= X2 – Y1
M= ∆ X

19. Finding the Slope
John first have to locate
the two points on the
line. We notice that the
line intersect at the y-
axis. This is the first
point (0, 4). When then
find the second point on
the line where the two
gridlines cross. This is
our second point (2, 1).

20. Now that we have our points John
plugs it into the slope equation to find
the slope.
M = (y2 – y1)/ (x2 – x1)
M = (1 – 4) / (2 – 0)
M = -3 / 2
The slope is negative.

21. Overall
John has taught us how to draw a line by
graphing the points and calculating the slope.
Know he and his friends can catch their flies.

22. Cited
This is the site where I found my lesson plan and
some of my graphs.
• http://mathforum.org/cgraph/cslope/drawlin
e.html
This is the site where I found some of my
graphs.
• http://nghsapphysicsb.blogspot.com/2009/10
/super-explanation-of-how-rolling.html