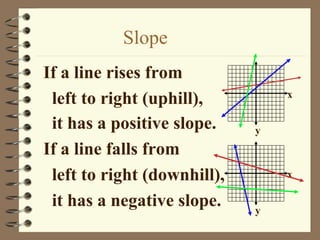
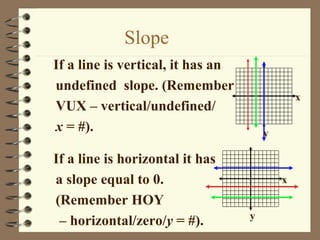
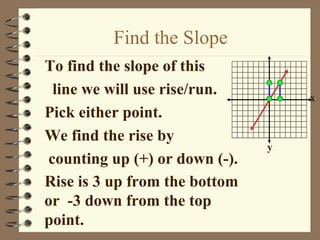
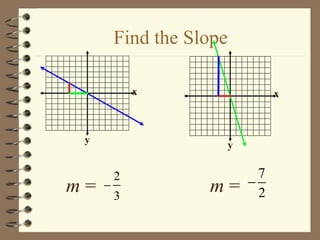
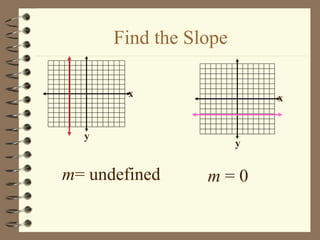
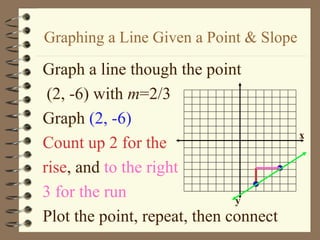
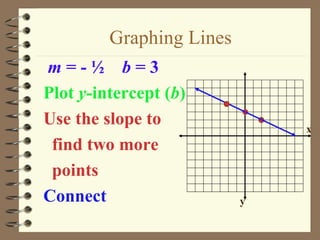
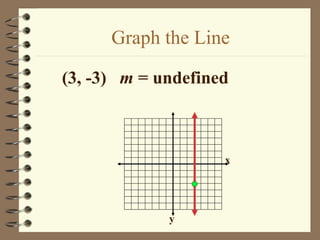
1. The document discusses slope and rate of change, including how to calculate slope from two points on a line and how to interpret positive, negative, zero, and undefined slopes. 2. It provides examples of finding the slope of lines from graphs and points, and discusses how to identify parallel and perpendicular lines based on their slopes. 3. The key concepts are how to determine the steepness of a line from its slope, and that parallel lines have the same slope while perpendicular lines have slopes that are opposite reciprocals.

1. Slope & Rate of Change
Calculator ONLY today!
Today’s objectives:
1. I will find slopes of lines.
2. I will classify parallel and
perpendicular lines.
3. I will determine which line is
steeper.

2. 2-2 Slope & Rate of Change
Slope
indicates the steepness of a line.
is “the change in y over the change in
x” (vertical over horizontal).
is the ‘m’ in y = mx + b.

3. Finding the Slope of a Line
rise
m= run
y2 − y1
m= x2 − x1
We use the first equation
when given a graph, the second
when given two points.

4. Slope
If a line rises from
left to right (uphill), x
it has a positive slope. y
If a line falls from
left to right (downhill), x
it has a negative slope. y

5. Slope
If a line is vertical, it has an
undefined slope. (Remember
x
VUX – vertical/undefined/
x = #). y
If a line is horizontal it has
a slope equal to 0. x
(Remember HOY
y
– horizontal/zero/y = #).

6. Find the Slope
To find the slope of this
line we will use rise/run. x
Pick either point.
We find the rise by
y
counting up (+) or down (-).
Rise is 3 up from the bottom
or -3 down from the top
point.

7. Find the Slope
To find the run, we
count right (+) or x
left (-).
If you started from the y
top point, your run will be left
-2, if you started at the bottom
point, your run will be right 2.

8. Find the Slope
So if you started with
the top point, your x
slope would be -3/-2.
If you started with the bottom y
point, your slope would be 3/2.
Are these the same? Yes!! The
slope of the line is 3/2.

9. Find the Slope
x x
y y
2 7
m= − m= −
3 2

10. Find the Slope
x x
y
y
m= undefined m=0

11. Find the Slope of the Line
Given the Given the
points (5, 1) & points (-6, -2)
(6, 4) & (-1, 0)
−2 − 0
m = 4 −1 m=
6−5 −6 − −1
3 −2 −2 2
= =3 = = =
1 −6 + 1 −5 5

12. Parallel Lines
What do you know about the slope
of parallel lines?
Parallel lines have the
SAME SLOPE!
What is the slope of the line
parallel to y = -2x + 4?
m = -2

13. Perpendicular Lines
What do you know about the slope
of perpendicular lines?
Perpendicular lines have slopes
that are opposite reciprocals!
What is the slope of the line
perpendicular to y = -2x + 4?
m = 1/2

14. Graphing a Line Given a Point & Slope
Graph a line though the point
(2, -6) with m=2/3
Graph (2, -6)
x
Count up 2 for the
rise, and to the right
3 for the run y
Plot the point, repeat, then connect

15. Graphing Lines
Graph the line perpendicular to
y = 2x + 3 that goes through the
point (-2, 3).
The slope of the line is 2 so the
slope of the perpendicular line is
-1/2.
m = -1/2 b = 3

16. Graphing Lines
m=-½ b=3
Plot y-intercept (b)
Use the slope to x
find two more
points
Connect y

17. Graphing Lines
Graph the line parallel to x = -1
that goes through the point
(3, -3).
The slope of the line is undefined
(VUX) so the slope of the parallel
line is undefined.

18. Graph the Line
(3, -3) m = undefined
x
y