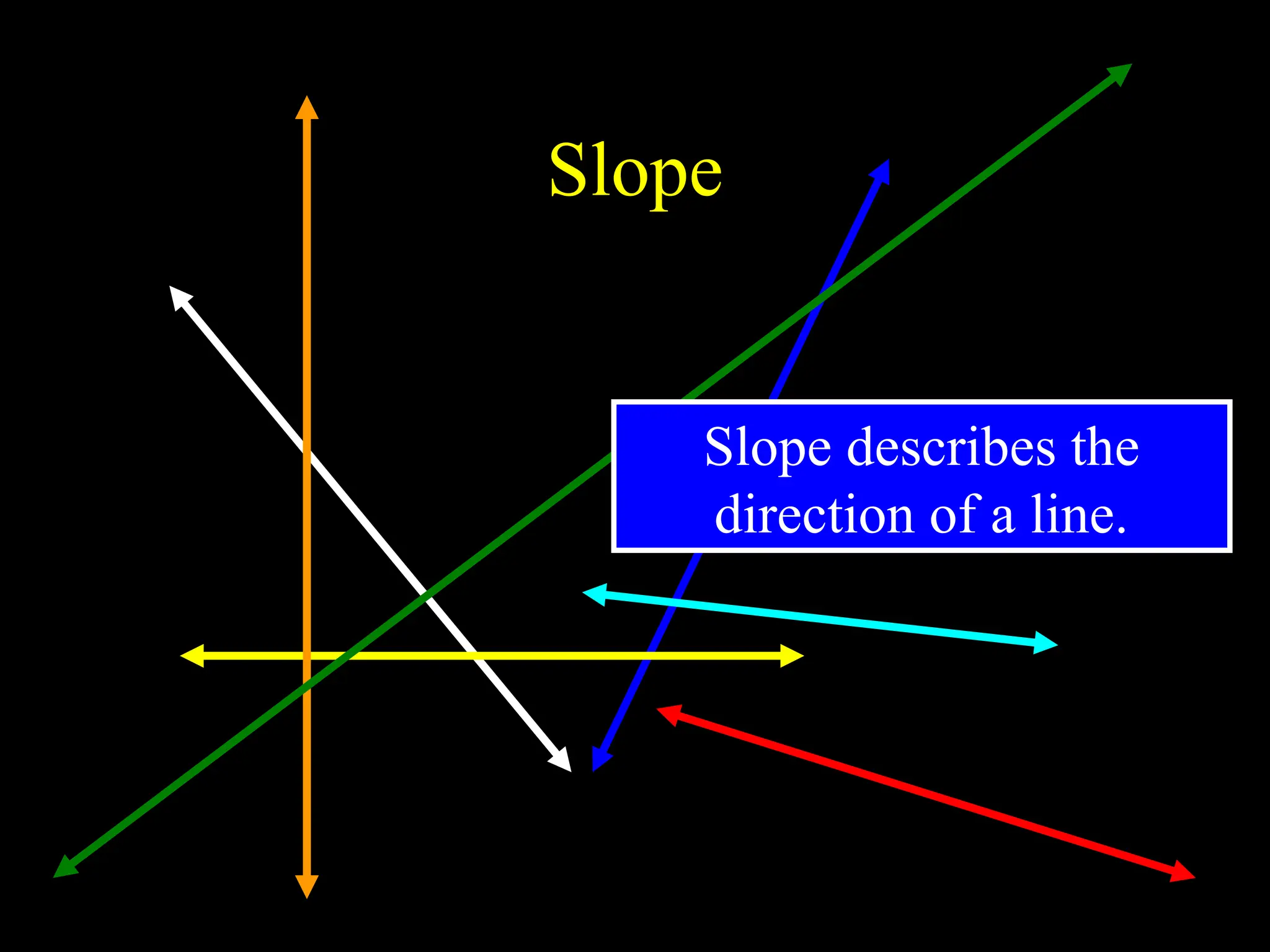
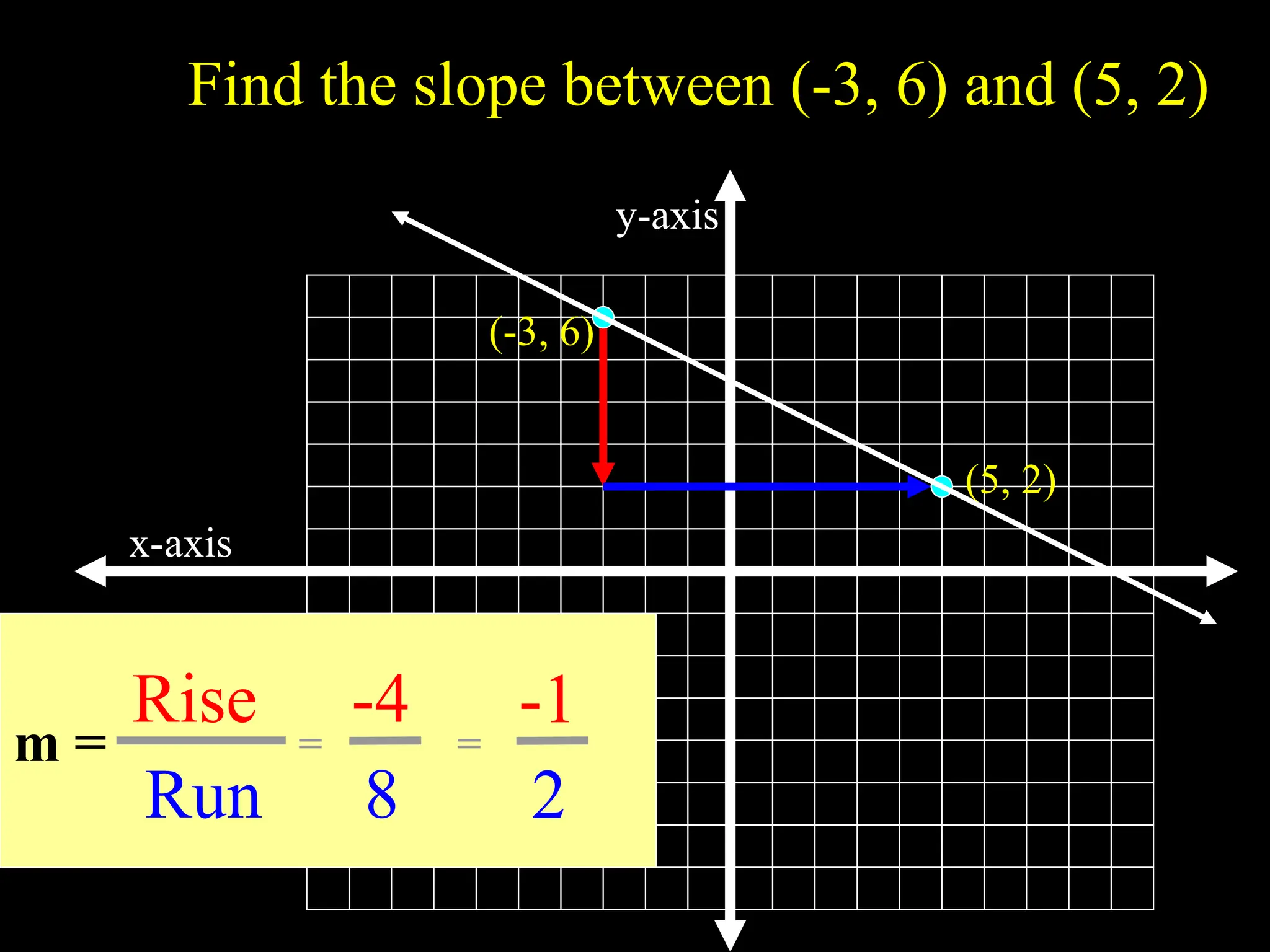
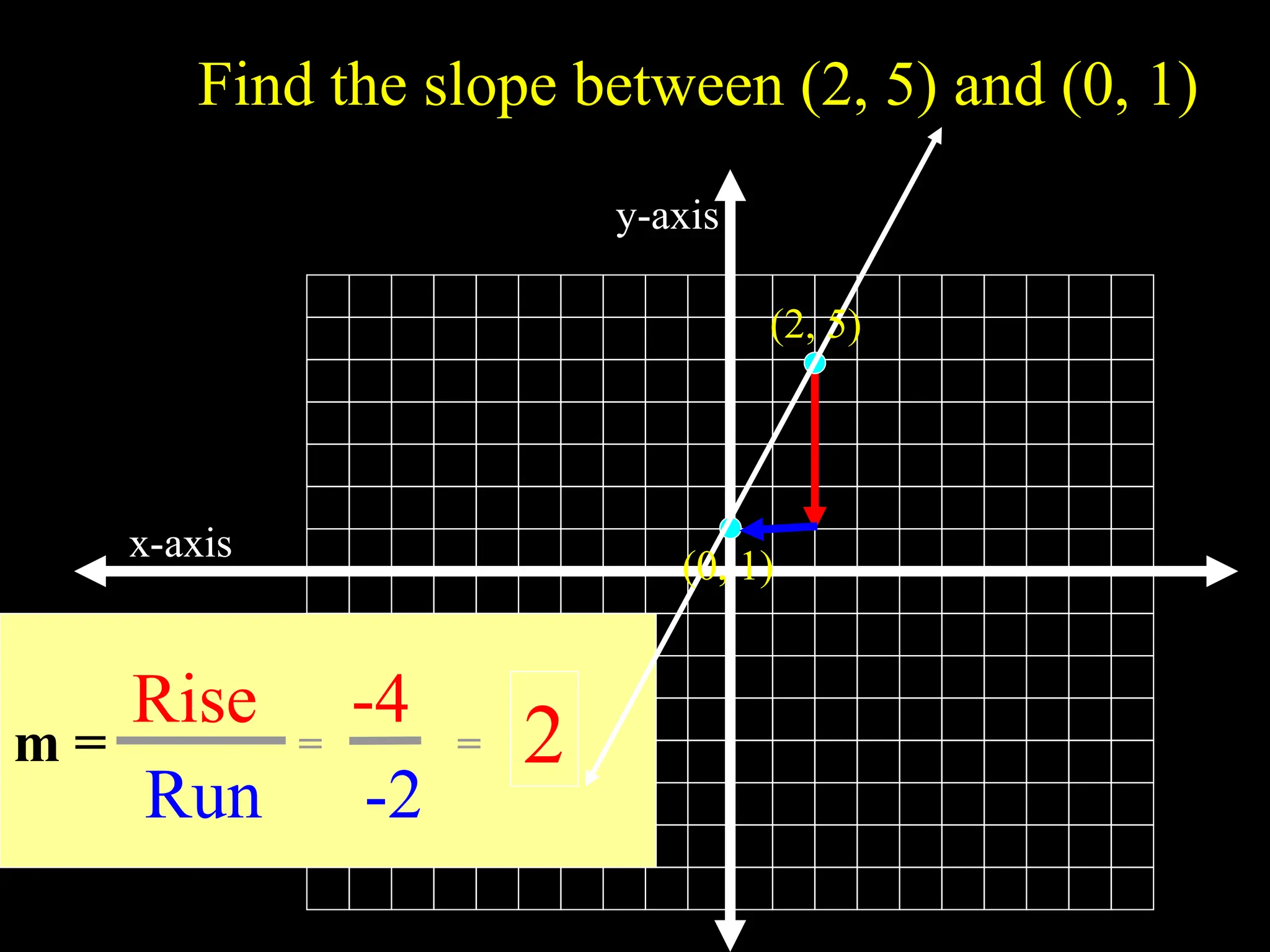
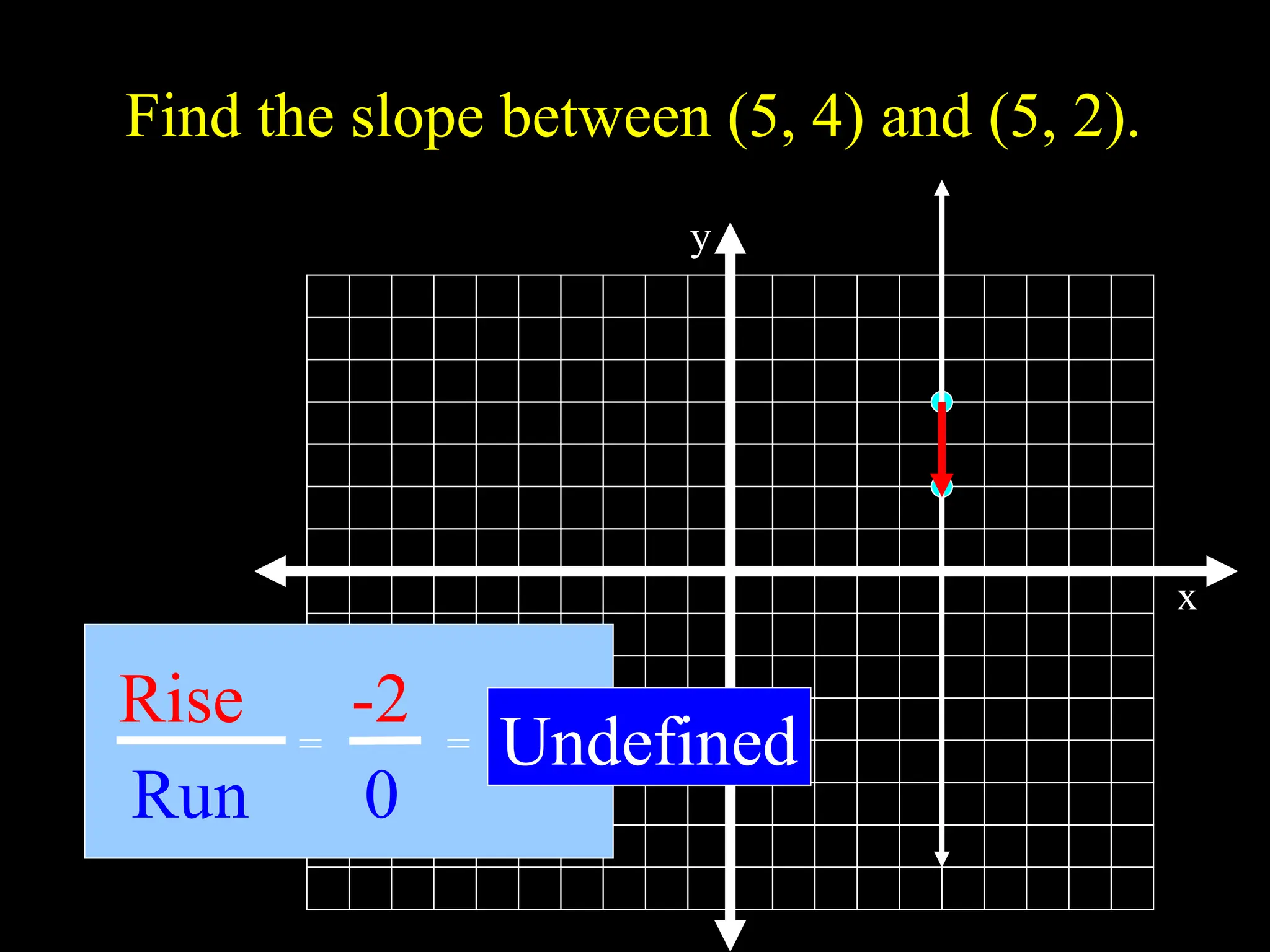
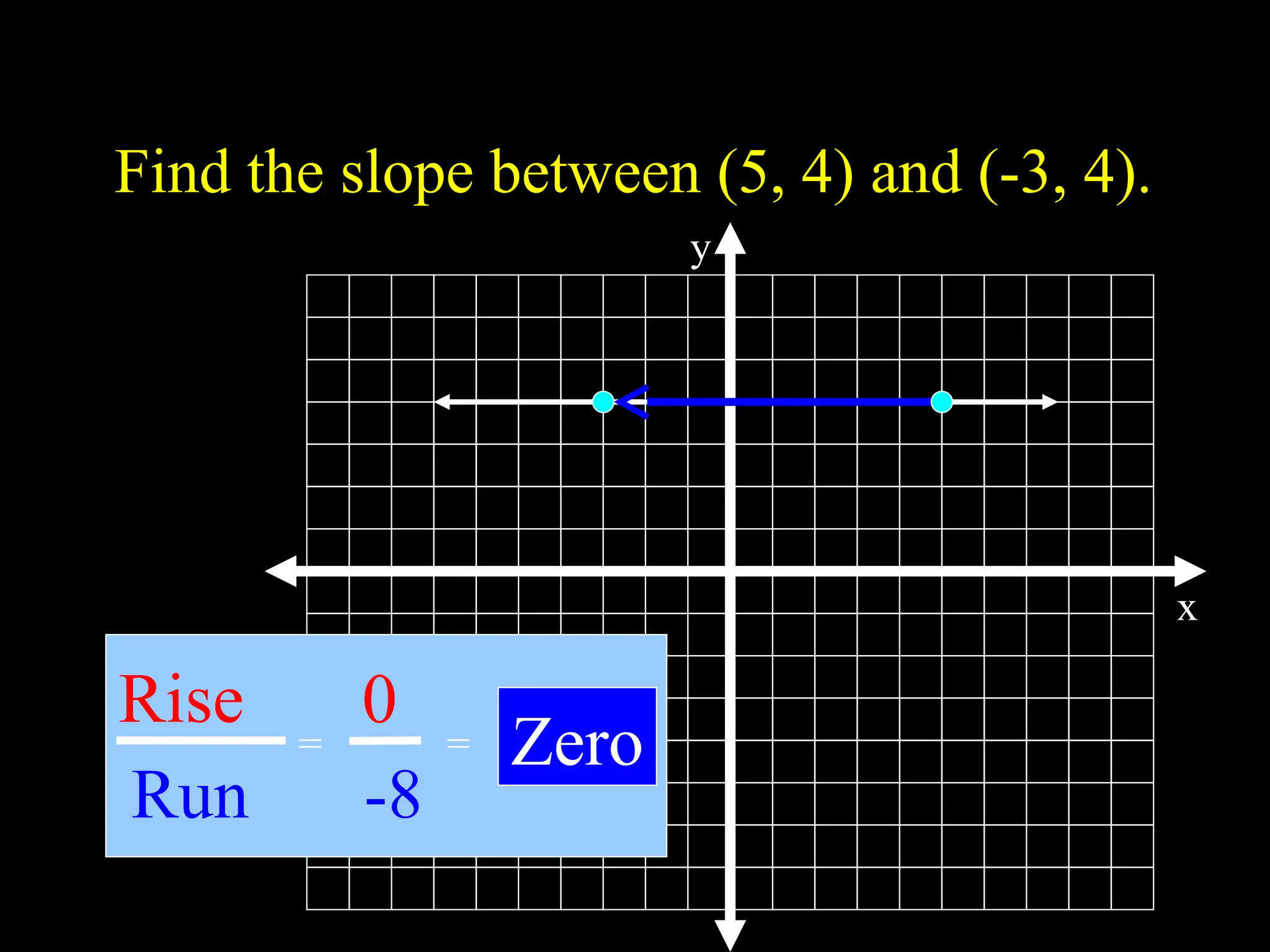
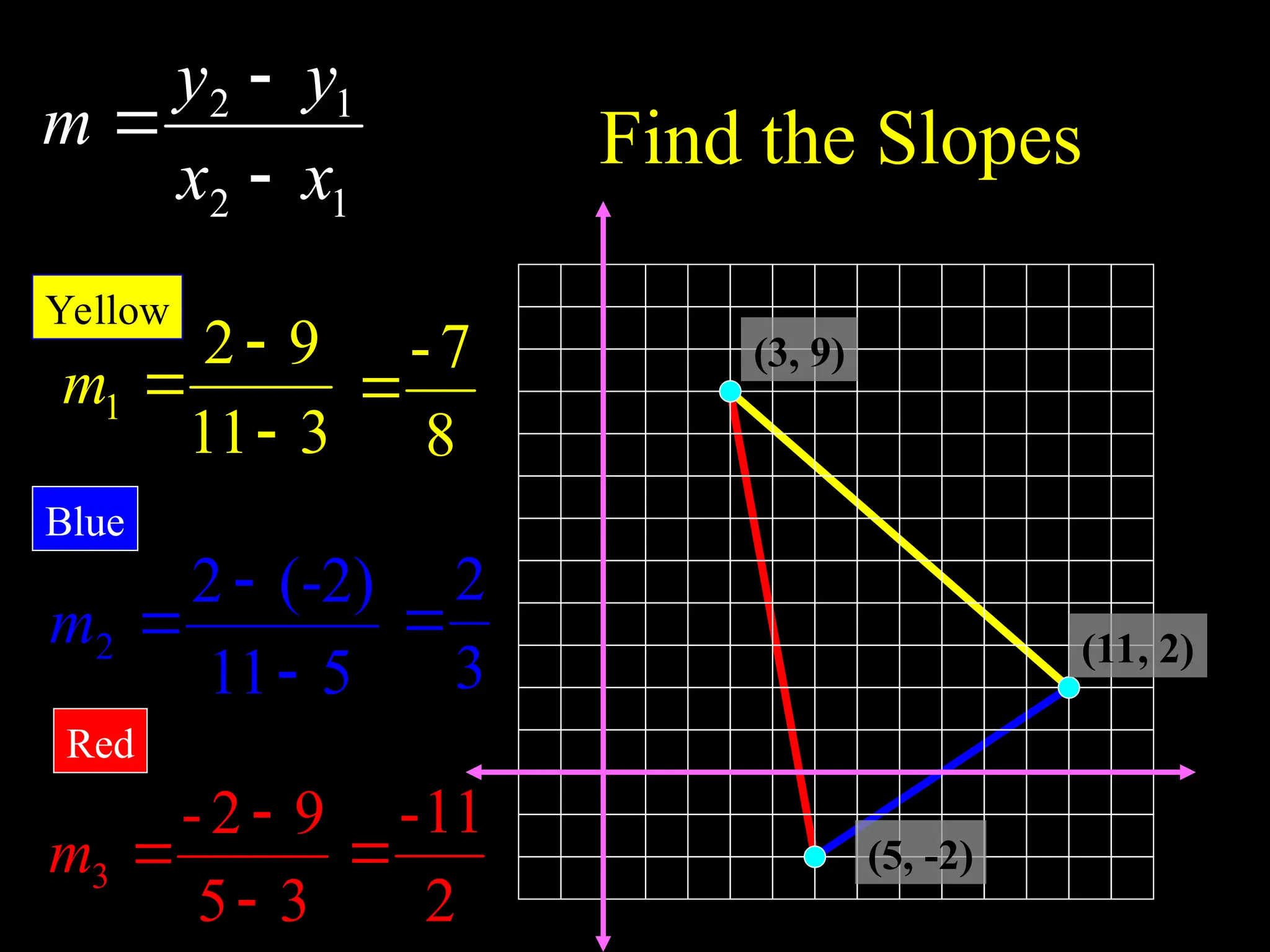
The document explains the concept of a line, detailing its definition as a set of points on a plane and the characteristics of its slope. It provides methods for calculating the slope between points, illustrating examples to show both negative and positive slopes, as well as undefined and zero slopes in special cases. The summary concludes with key attributes of vertical and horizontal lines regarding their slopes and intercepts.

1. What is a Line?
• A line is the set of points forming a straight
path on a plane
• The slant (slope) between any two points on
a line is always equal
• A line on the Cartesian plane can be
described by a linear equation
x-axis
y-axis

2. Definition - Linear Equation
• Any equation that can be put into the form
Ax + By  C = 0, where A, B, and C are
Integers and A and B are not both 0, is called
a linear equation in two variables.
• The graph will be a straight line.
• The form Ax + By  C = 0 is called general
form (Integer coefficients all on one side = 0)

3. Slope
Slope describes the
direction of a line.

4. Slope (m)
• It is describes the steepness of the
line. It is also the ratio of rise to
run.
1
2
1
2
x
x
y
y
x
in
change
y
in
change
run
rise
slope






5. Example 1:
Calculate the slope between (-3, 6) and (5, 2)
1
2
1
2
x
x
y
y
m



)
3
-
(
)
5
(
)
6
(
)
2
(



m
8
4
-

2
1
-

x1 y1 x2 y2
We use the letter m
to represent slope
m

6. x-axis
y-axis
Find the slope between (-3, 6) and (5, 2)
Rise
Run
-4
8
-1
2
= =
(-3, 6)
(5, 2)
m =

7. From this result, we can see that...
•If the line falls to the
right, the slope is
negative.

8. Example 2:
Calculate the slope between (2, 5) and (0, 1)
1
2
1
2
x
x
y
y
m



x1 y1 x2 y2
We use the letter m
to represent slope
m

9. x-axis
y-axis
Find the slope between (2, 5) and (0, 1)
Rise
Run
-4
-2
2
= =
(2, 5)
(0, 1)
m =

10. From this result, we can see that...
•If the line falls to the
left, the slope is
positive.

11. Example 3:
Find the slope between (5, 4) and (5, 2).
1
2
1
2
x
x
y
y
m



)
5
(
)
5
(
)
4
(
)
2
(



m
0
2
-

STOP
This slope is undefined.
x1 y1 x2 y2

12. x
y
Find the slope between (5, 4) and (5, 2).
Rise
Run
-2
0
Undefined
= =

13. Example 4:
Find the slope between (5, 4) and (-3, 4).
1
2
1
2
x
x
y
y
m



)
5
(
)
3
-
(
)
4
(
)
4
(



m
8
-
0

This slope is zero.
x1 y1 x2 y2
0


14. x
y
Rise
Run
0
-8
Zero
= =
Find the slope between (5, 4) and (-3, 4).

15. From these results we
can see...
•The slope of a vertical
line is undefined.
•The slope of a
horizontal line is 0.

16. Find the Slopes
(5, -2)
(11, 2)
(3, 9)
1
2
1
2
x
x
y
y
m



3
11
9
2
1



m
Yellow
5
11
)
2
-
(
2
2



m
Blue
3
5
9
2
-
3



m
Red
8
7
-

3
2

2
11
-


17. Sign of the Slope
Which have a
positive slope?
Green
Blue
Which have a
negative slope?
Red
Light Blue
White
Undefined
Zero
Slope

18. Summary
• Vertical line
– Slope is undefined
– x-intercept is (x, 0)
– no y-intercept
• Horizontal line
– Slope is 0.
– y-intercept is (0, y)
– no x-intercept