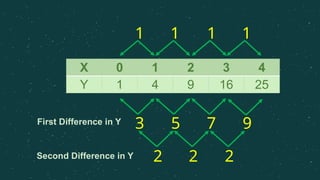
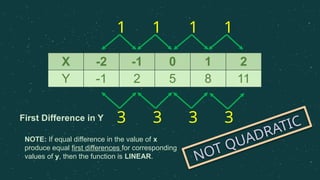
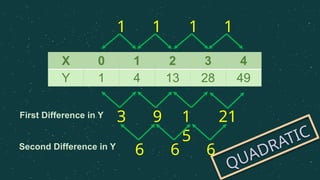
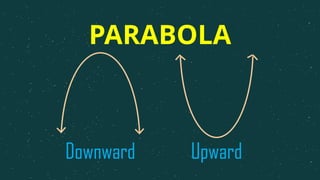
The document introduces quadratic functions, defined in the form f(x) = ax² + bx + c, emphasizing the conditions for identifying quadratic behavior through table values and second differences. It explains how to graph these functions, which produce a parabolic curve that can open upward or downward and vary in steepness. Examples are provided to illustrate the calculations of y values for specific x inputs in quadratic functions.

1. MATH 9
WELCOME TO OUR CLASS!

2. What is
Quadratic
Function?
 A quadratic function has the form f(x)
= ax² + bx + c, whre a, b, and c, are real
numbers and a ≠ 0.
 “f(x) =” is a classical way of writing a
function.

3. Table of
Values
 Quadratic can also be presented in table, it consist
the values of x and y.
 If equal difference in the value of x produce equal
second differences for corresponding values of y,
then given table represents QUADRATIC.
f(x) = ax² +
bx + c

4. X 0 1 2 3 4
Y
f(x) = x² + 5x + 6
y = (0)² + 5(0) + 6
y = 0 + 0 + 6
y = 6
INDEPENDENT
DEPENDENT 6
y = (1)² + 5(1) +
6
y = 1 + 5 + 6
y = 12
12
y = (2)² + 5(2) + 6
y = 4 + 10 + 6
y = 20
20 30 42

5. X 0 1 2 3 4
Y 1 4 9 16 25
1 1 1 1
3 5 7 9
2 2 2
First Difference in Y
Second Difference in Y

6. X -2 -1 0 1 2
Y -1 2 5 8 11
1 1 1 1
3 3 3 3
First Difference in Y
NOT QUADRATIC
NOTE: If equal difference in the value of x
produce equal first differences for corresponding
values of y, then the function is LINEAR.

7. X 0 1 2 3 4
Y 1 4 13 28 49
1 1 1 1
3 9 1
5
21
6 6 6
First Difference in Y
Second Difference in Y
QUADRATIC

8. Quadratic
Function
The graph of a quadratic function is a curve
called a parabola. It may open upward or
downward and vary in "width" or "steepness",
but they all have the same basic "U" shape.

9. PARABOLA
Downward Upward

10. HOW TO GRAPH A
QUADRATIC
FUNCTION?

11. X -4 -2 0 2 4
Y
f(x) = x² + 5x + 6
2 0 6 20 42
y = (-2)² + 5(-2) +
6
y = 4 - 10 + 6
y = 0
y = (0)² + 5(0) + 6
y = 0 + 0 + 6
y = 6
y = (2)² + 5(2) + 6
y = 4 + 10 + 6
y = 20
y = (4)² + 5(4) + 6
y = 16 + 20 + 6
y = 42
y = (-4)² + 5(-4) + 6
y = 16 - 20 + 6
y = 2

12. X -3 -2 -1 0 1
Y
f(x) = x² + 4x + 4