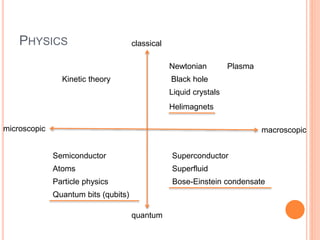
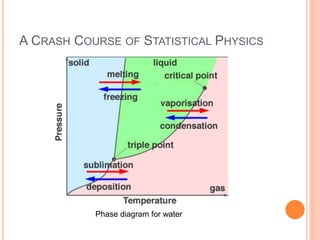
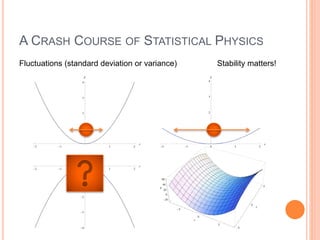
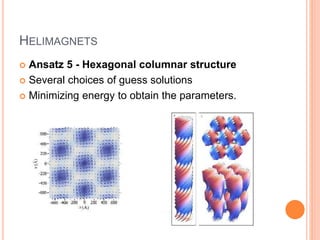
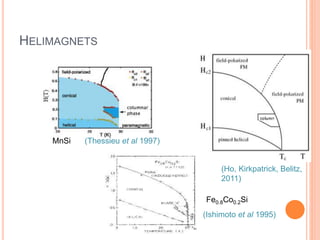
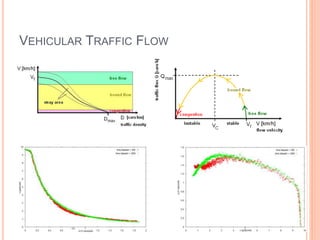
The document discusses optimization in statistical physics, focusing on metallic helimagnets and other projects such as two-dimensional Bose gas and ultra-high energy cosmic rays. It covers the importance of partition functions, free energy, and phase diagrams in understanding many-body systems, as well as vehicular traffic flow modeling using statistical mechanics. Acknowledgments are made to various collaborators and institutions involved in the research.

1. OPTIMIZATION IN STATISTICAL
PHYSICS
Kwan-Yuet Ho
Institute for Physical Science and Technology &
Department of Physics
University of Maryland
9/27/2012

2.  PhD (Physics), University of Maryland
Thesis: Properties of Metallic Helimagnets
Field: Condensed Matter Physics, Statistical Physics
 BSc (Physics & Math), Chinese University of Hong
Kong
Thesis: Quantum Entanglement of Continuous Systems
Field: Quantum Physics, Mathematical Physics
Other projects:
 Two-dimensional Bose gas
(Condensed Matter Physics, Statistical Physics,
Atomic Physics, Quantum Physics)
 Ultra-high Energy Cosmic Rays
(Particle Astrophysics)

3. PHYSICS
Classical Mechanics
Relativistic Mechanics
Quantum Mechanics
(Bose-Einstein condensate)

4. PHYSICS
String Theory (Calabi-
Yau space)
Superfluid
Liquid Crystals

5. PHYSICS
 Classical vs Quantum
 Deterministic vs
probabilistic
 Continuous vs Discrete
I think it is safe to say that
no one understands
Quantum Mechanics. –
Richard Feynman

6. PHYSICS
 Microscopic vs Macroscopic
 N << or ~ 1023
 Few-body vs Many-body

7. PHYSICS
macroscopicmicroscopic
classical
quantum
Newtonian
Black hole
Plasma
Liquid crystals
Helimagnets
Superconductor
Superfluid
Bose-Einstein condensate
Semiconductor
Atoms
Particle physics
Quantum bits (qubits)
Kinetic theory

8. A CRASH COURSE OF STATISTICAL PHYSICS
 Statistical Physics/Mechanics: the study of a
system containing many (N~1023) particles, using
probability theory and statistics
 Fixed N, V and T, probability of a state m is given
by
Partition Function
Information such as T, <E>
and other measurable
quantities
Normalization
constant

9. A CRASH COURSE OF STATISTICAL PHYSICS
Helmholtz free energy F
We model the free energy F, a summary of all the information about the
system!
Appropriate F is the minimized E(x) one with respect to m or x, to get
the expected measured value of m and x.
Method of steepest descent / mean field theory / equation of motion

10. A CRASH COURSE OF STATISTICAL PHYSICS
Phase diagram for water

11. A CRASH COURSE OF STATISTICAL PHYSICS
Stability matters!Fluctuations (standard deviation or variance)

12. A CRASH COURSE OF STATISTICAL PHYSICS
Fluctuations and stability are studied by perturbation:
Putting it back to the free energy, and studying its variance.

13. A CRASH COURSE OF STATISTICAL PHYSICS

14. A CRASH COURSE OF STATISTICAL PHYSICS
True kind of problem I am dealing with.
Perturbation does not only lead to variance but also
correlations, <M(x) M(x’)>.
Hamiltonian functional

15. HELIMAGNETS
 Leonard: What would you be if you were attached
to another object by an inclined plane, wrapped
helically around an axis?
 Sheldon: Screwed.

16. HELIMAGNETS
 Helimagnets, or helical magnets, are magnets with
magnetic dipoles aligned helically.
 Good for computer memories because of its non-
volatility.

17. HELIMAGNETS
 Landu-Ginzburg-Wilson (LGW) functional
 Minimizing H: mean-field theory (for SFM and SDM)

18. HELIMAGNETS
 Optimize the solution for M to minimize the energy
 Phase diagram
 But the full solution is very difficult to find!!!!!!
 We identify the solutions from measurement
(ansatz).

19. HELIMAGNETS
 Ansatz 1 - Something like bar magnets: M=Mz
 Equation: rM+uM3-H=0
 Numerically find all the “optimized” solutions, and
reject those that are invalid and that does not give
the minimum energy.

20. HELIMAGNETS
Equation to solve
Finding minimum energy
Finding optimized M

21. HELIMAGNETS
 Ansatz 2 - Helical phase:
M=m0 (cos(qz)x+sin(qz)y)
 Ansatz 3 - Conical phase:
M=m0 (cos(qz)x+sin(qz)y)+mlz
 Solve for m0 and ml.
 Closed forms available.

22. HELIMAGNETS
 Ansatz 4 - Perpendicular helix: tested, and found
not to be valid.
 No closed form available.
 Numerically solve three equations, discarding
invalid data, discarding data with larger energies.
Equations to solve

23. HELIMAGNETS
Finding minimum energy
Finding optimized M

24. HELIMAGNETS
 Ansatz 5 - Hexagonal columnar structure
 Several choices of guess solutions
 Minimizing energy to obtain the parameters.

25. HELIMAGNETS
 In my program, all the postulated solutions are
considered.
 The code decides the solution by checking which
has the lowest energy.

26. HELIMAGNETS
26
(Thessieu et al 1997)MnSi
(Ishimoto et al 1995)
Fe0.8Co0.2Si
(Ho, Kirkpatrick, Belitz,
2011)

27. VEHICULAR TRAFFIC FLOW
 Traffic is a big problem in Washington DC.

28. VEHICULAR TRAFFIC FLOW
time

29. VEHICULAR TRAFFIC FLOW
 Nagel-Schreckenberg
(NaSch) rule
 Step 1: Acceleration
vn -> min(vn+1, vmax)
 Step 2: Braking
vn -> min(vn, gn)
 Step 3: Randomization
vn -> max(vn-1,0) with a
probability p
Next node(s)

30. VEHICULAR TRAFFIC FLOW
 2-lane highway
 Lane-switching rule: At
cell i, find the distance
of the next barrier (a
car, a red traffic light,
the end of a road)
ahead for both lanes 0
(d0) and 1 (d1).
 On lane 0, switch to
lane 1 if d1>d0, and
vice versa.

31. VEHICULAR TRAFFIC FLOW

32. CONCLUSION
 Statistical physics is the study of many-body
physics using probability theory and statistics.
 The phase of the matter is the minimized energy of
the system. Finding the phase is an optimization
problem.
 The stability of the system depends on its variance
and correlation.
 The flow of traffic can be verified by microscopic
simulation by implementing linked list.

33. ACKNOWLEDGMENTS
 Theodore Kirkpatrick (University of Maryland)
 Dietrich Belitz (University of Oregon)
 Bei-lok Hu (University of Maryland)
 Esteban Calzetta (Universidad de Buenos Aires)
 Yan Sang (University of Oregon)
 Chi Kwong Law (Chinese University of Hong Kong)
 Lin Tian (University of California, Merced)
 Robert McKweon (Jefferson Lab)