Download as PDF, PPTX
![PHYS 624: Quick and Dirty Introduction to Mott Insulators
Static vs. Dynamic
Mean-Field Theory
Static = Hartree-Fock or Density Functional Theory:
Dynamic = Dynamical Mean-Field Theory:
3
2
3 3
[ ( )] [ ( )] ( ) ( )
( ) ( ) ( )1 ( ) ( ) 2[ ( )]
2 | |
kinetic ext
KS i
exchange
E V d
V
md d E
ρ ρ ρ
ερ ρ
ρ
Γ = +
⇒ + Ψ = Ψ′
′+ +
′−
∫
∫
r r r r r
r r rr r
r r r
r r
ℏ
23
[ ( )]( )
[ ( )] ( ) , ( ) ( )| ( )|
| | ( )
exchange
KS ext i i
i
E
V V d f
δ ρρ
ρ ρ ε
δρ
′
′= + + = Ψ
′−
∑∫
rr
r r r r r
r r r
[ ]
3
1
3 3
[ ( ), ] [ ( ), ] ( ) ( ) [ ( )] [ ( )]
1 ( ) ( )
[ ( ), ] [ ( )] ( ) 1/ [ ( )]2 | |
kinetic ext
exchange
G E G V d G t
d d E G G
ρ ρ ρ ω ω ω
ρ ρ
ρ ω ω ω ω
−Γ = + ∆ = − Σ ∆ −
⇒ ′
′+ + Σ ∆ ≡ ∆ − ∆ +′−
∫ ∑
∫
k
k
r r r r r
r r
r r r
r r](https://image.slidesharecdn.com/mottinsulators-170123200300/75/Quick-and-Dirty-Introduction-to-Mott-Insulators-18-2048.jpg)
Uploaded byABDERRAHMANE REGGAD
Quick and Dirty Introduction to Mott Insulators
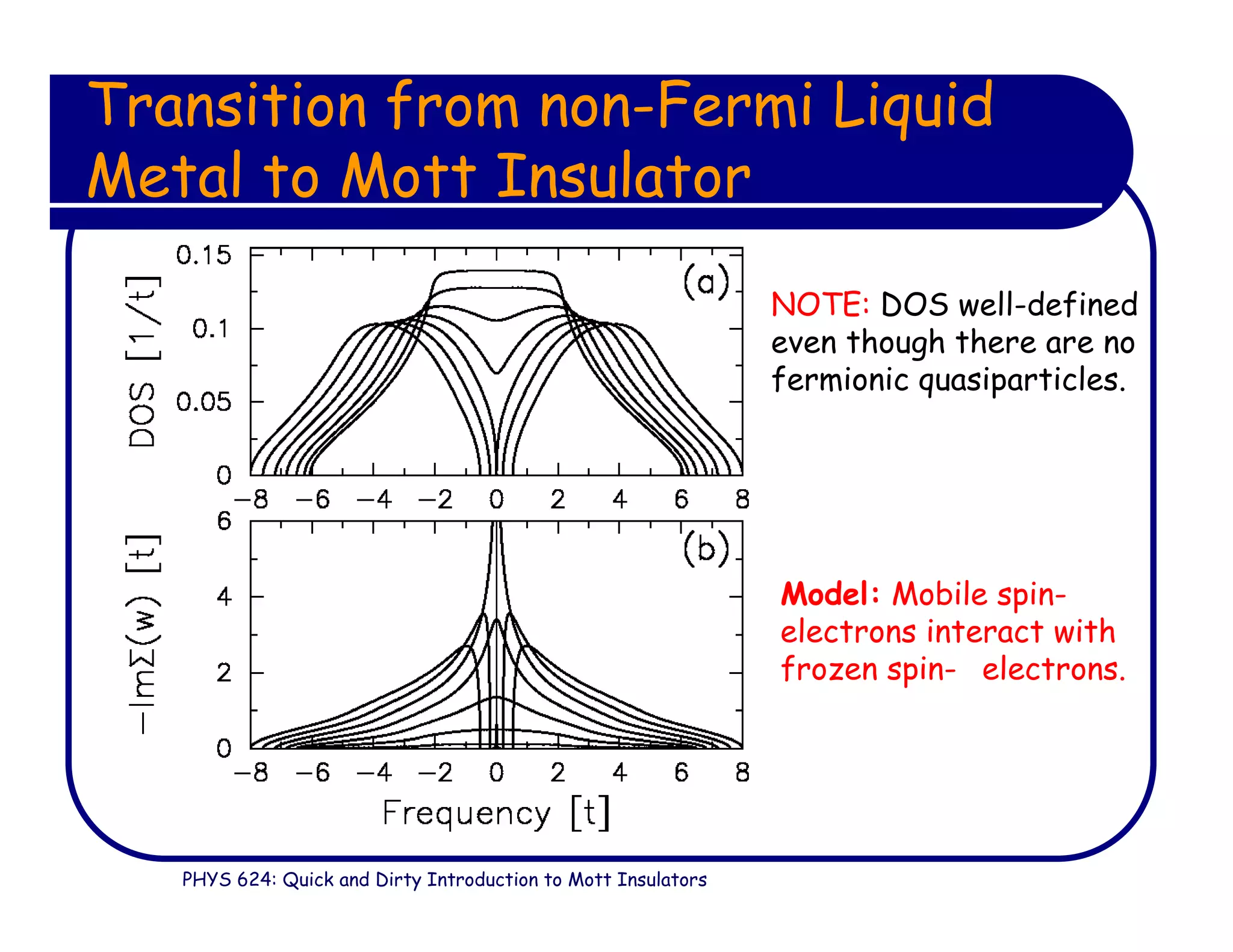
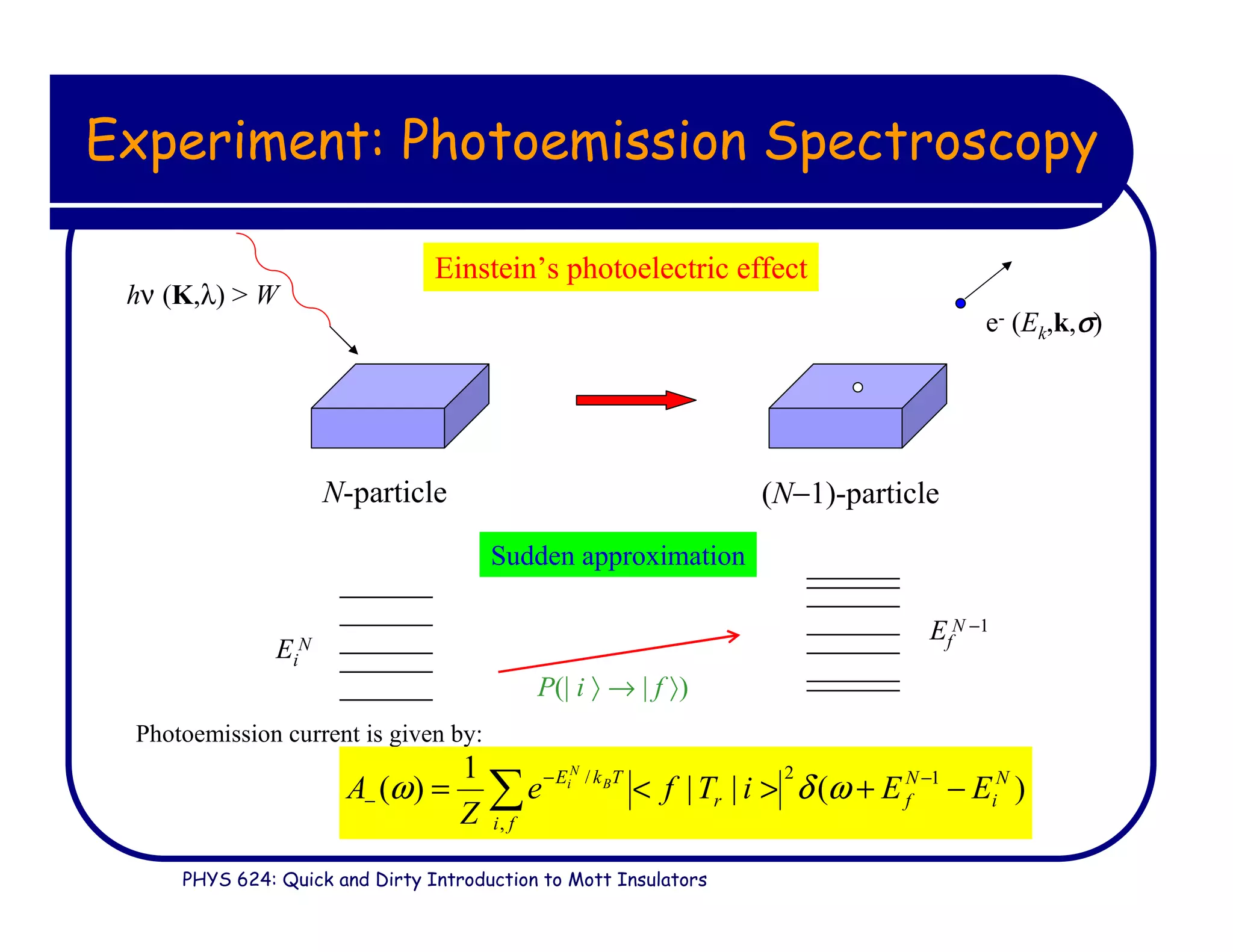
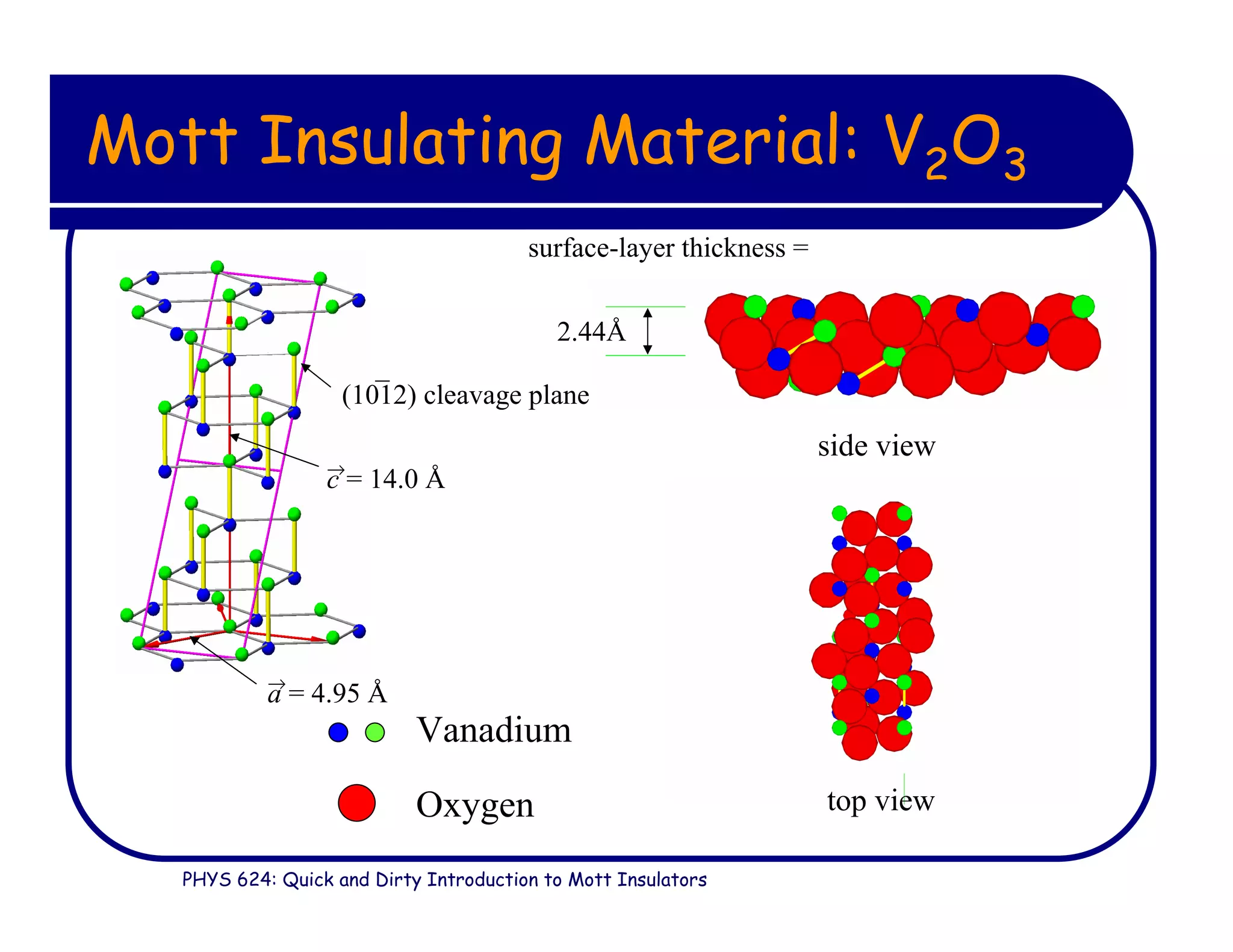
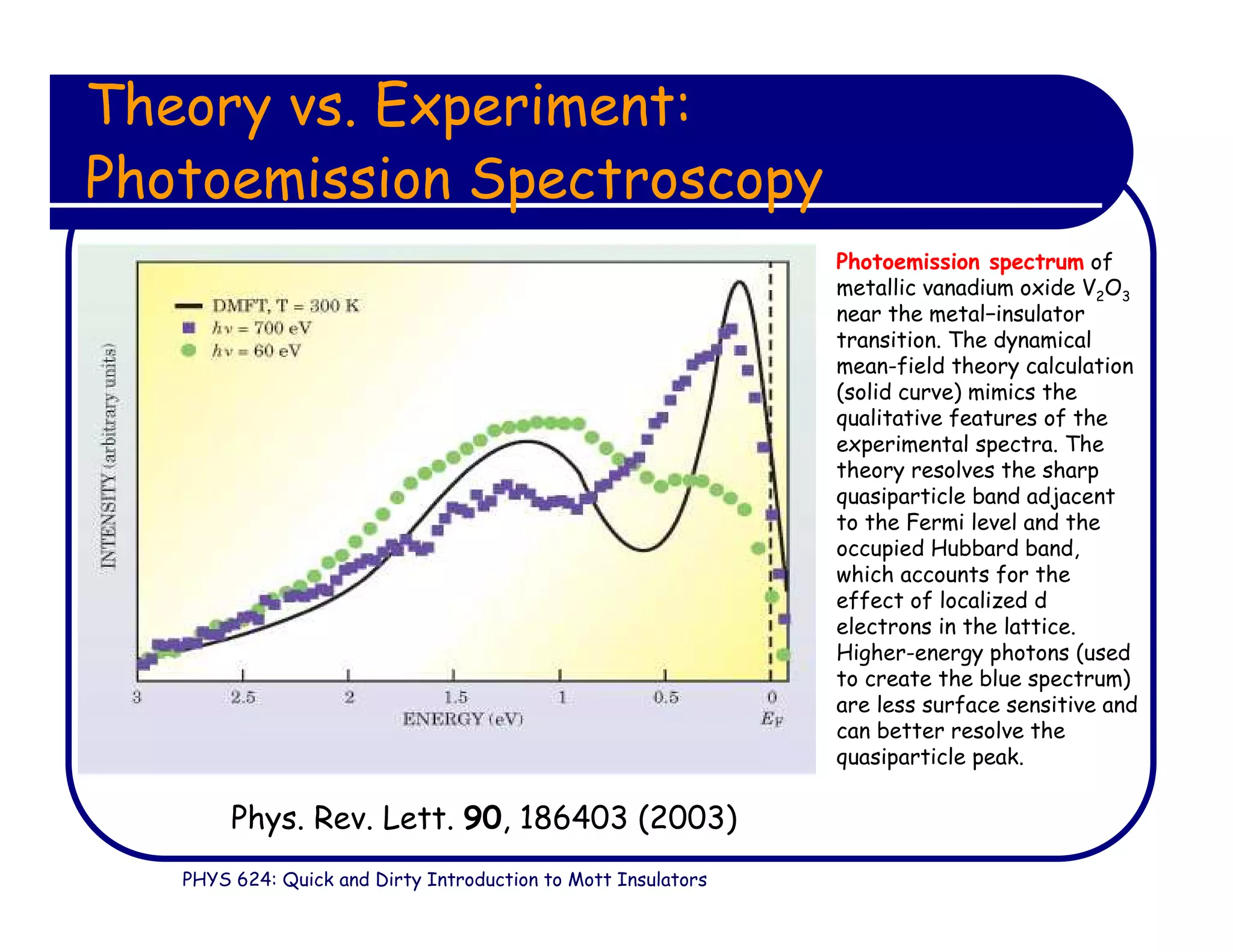
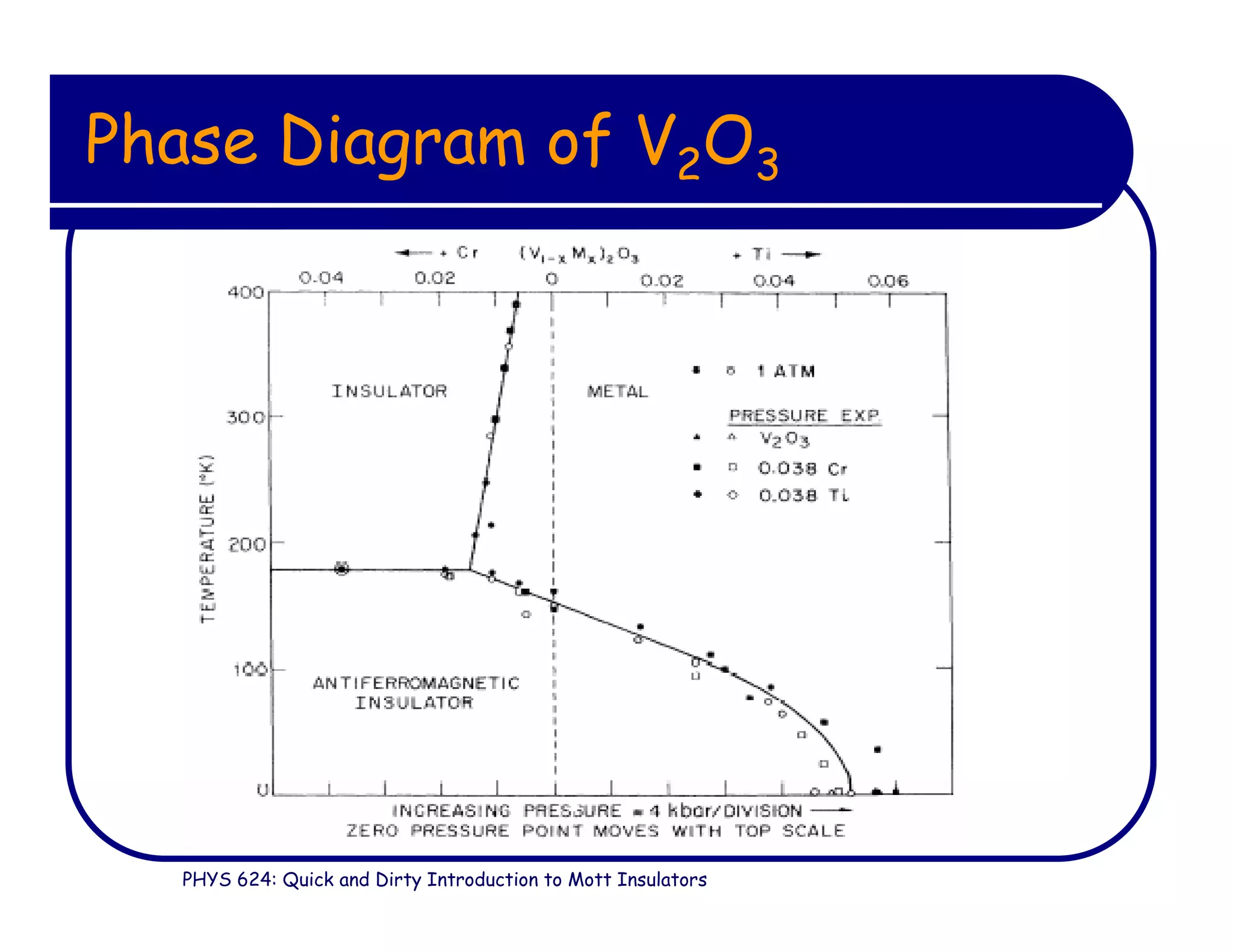
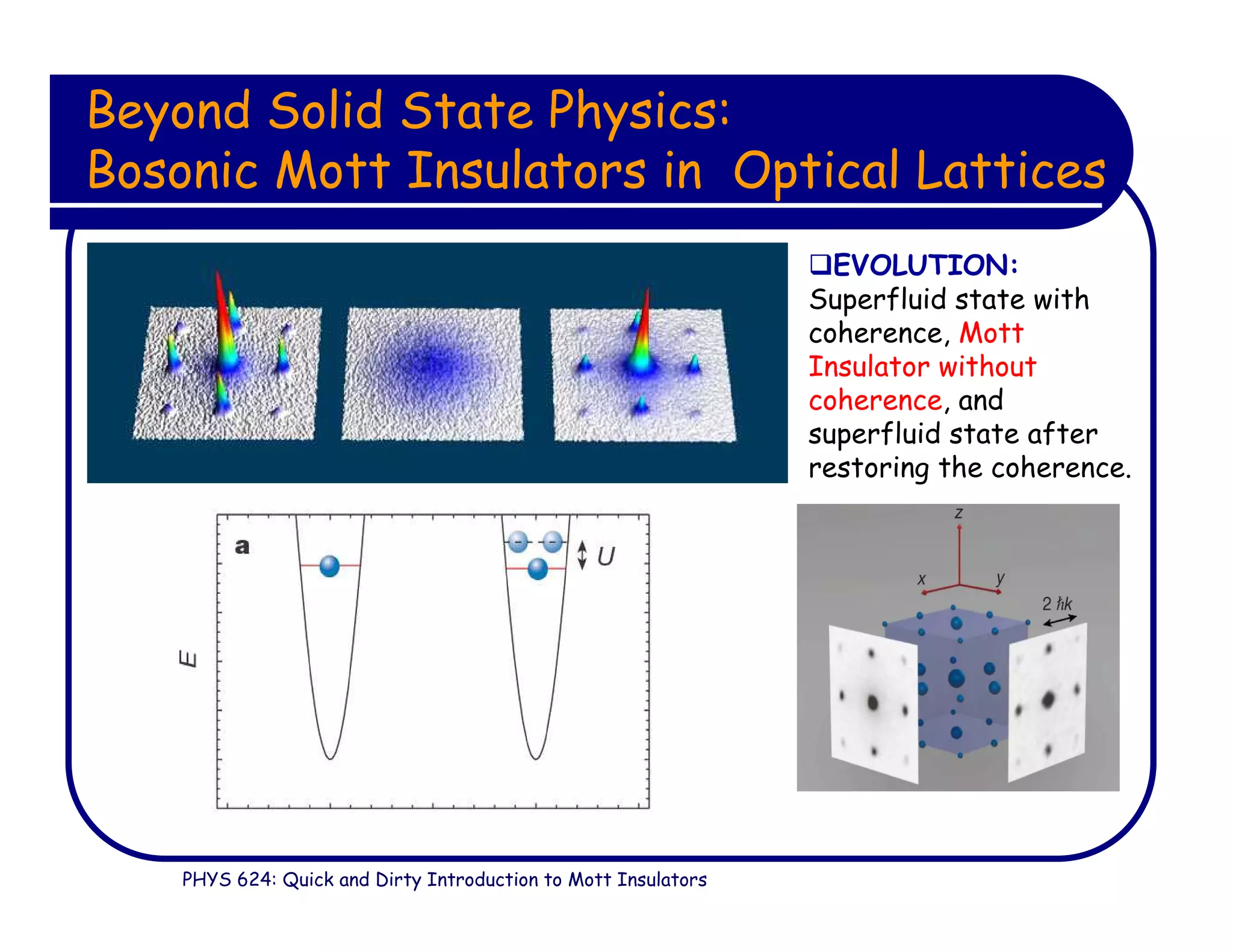
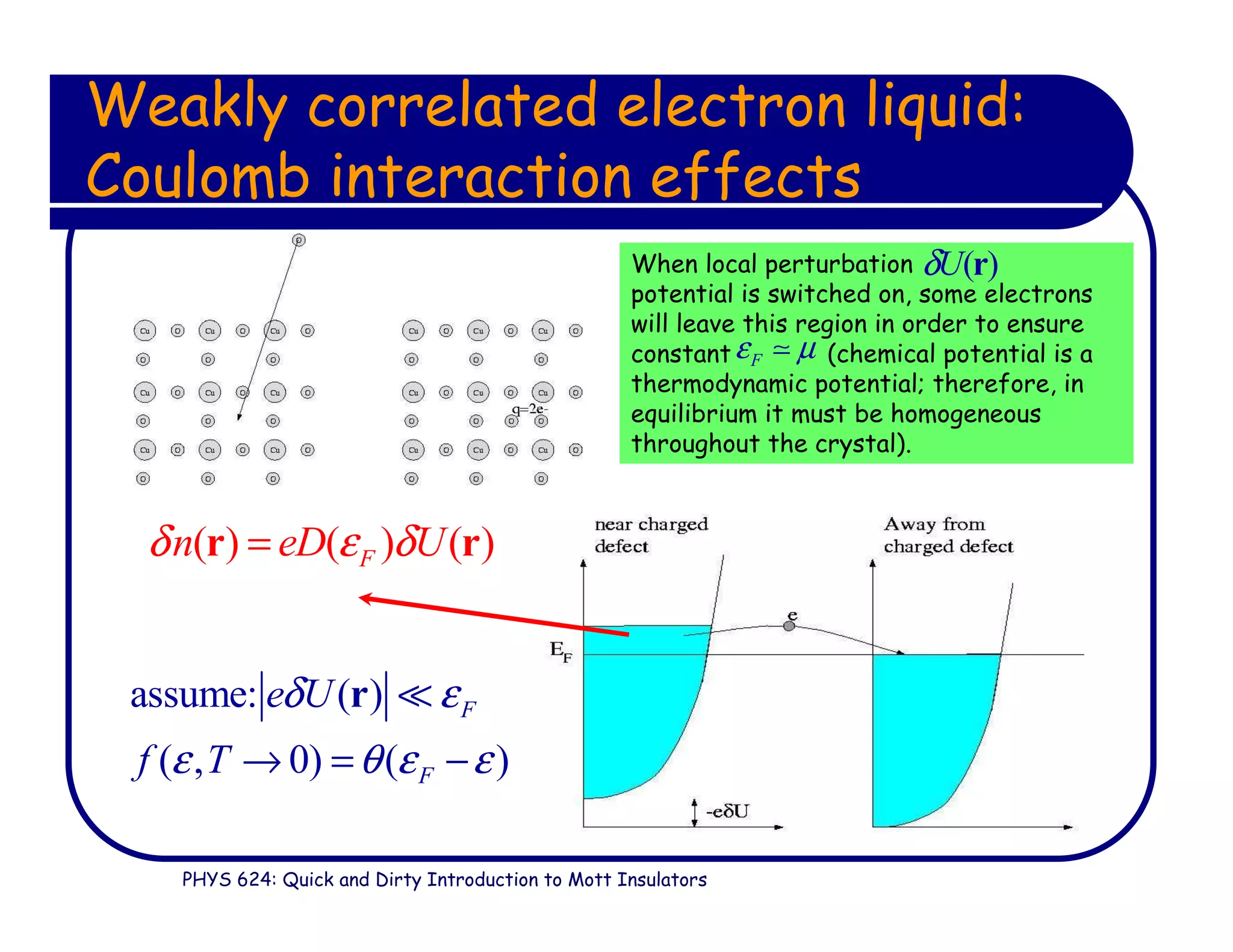
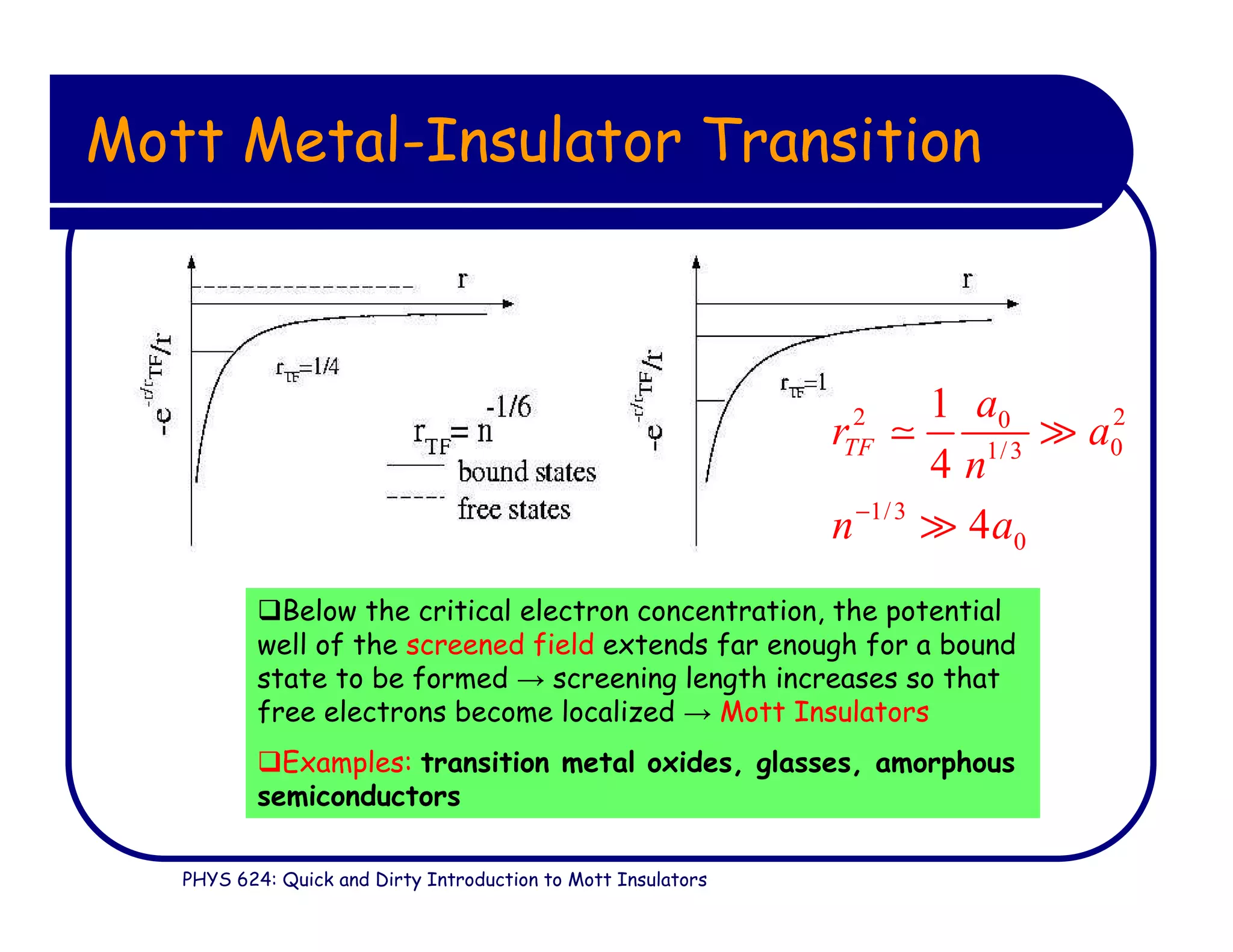
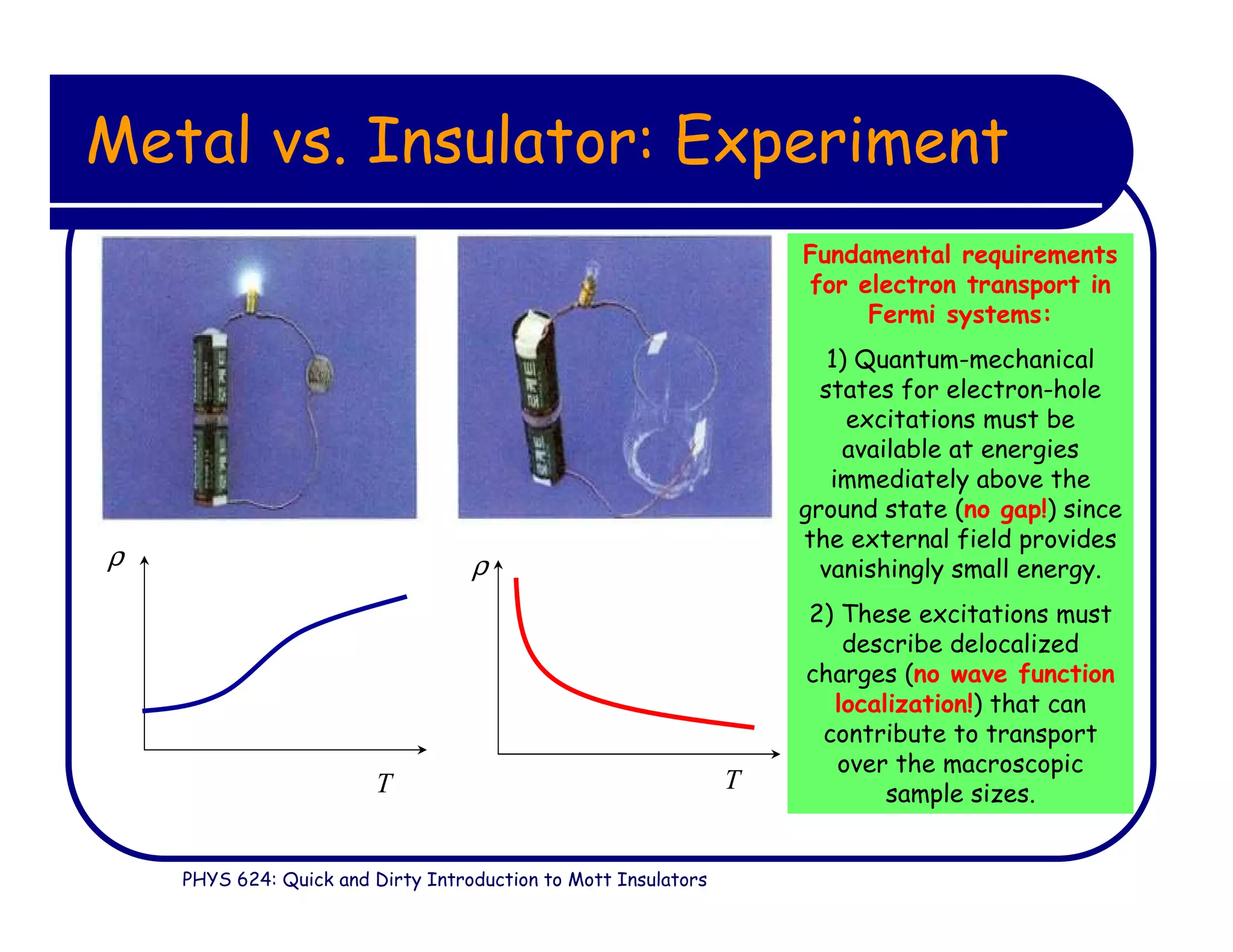
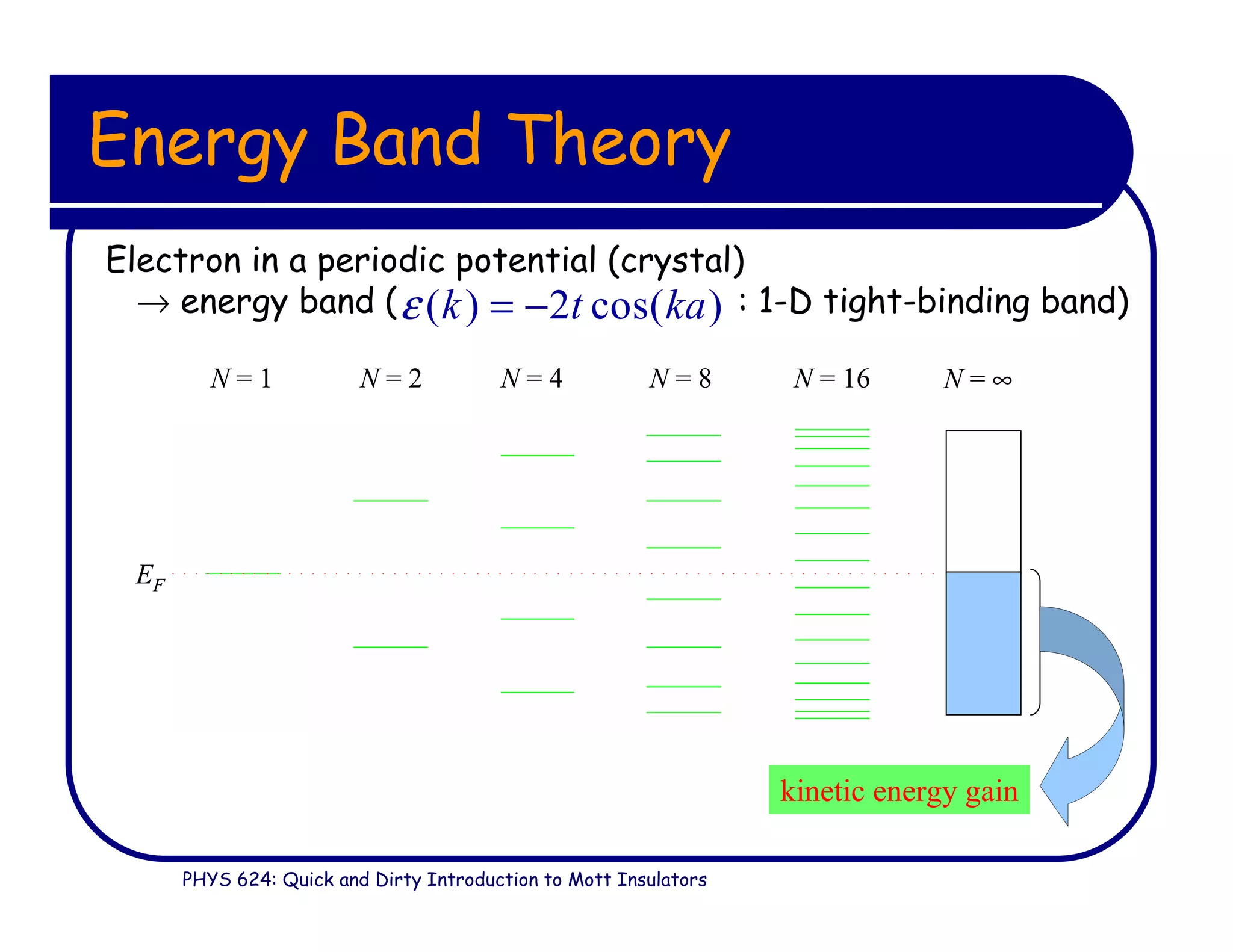
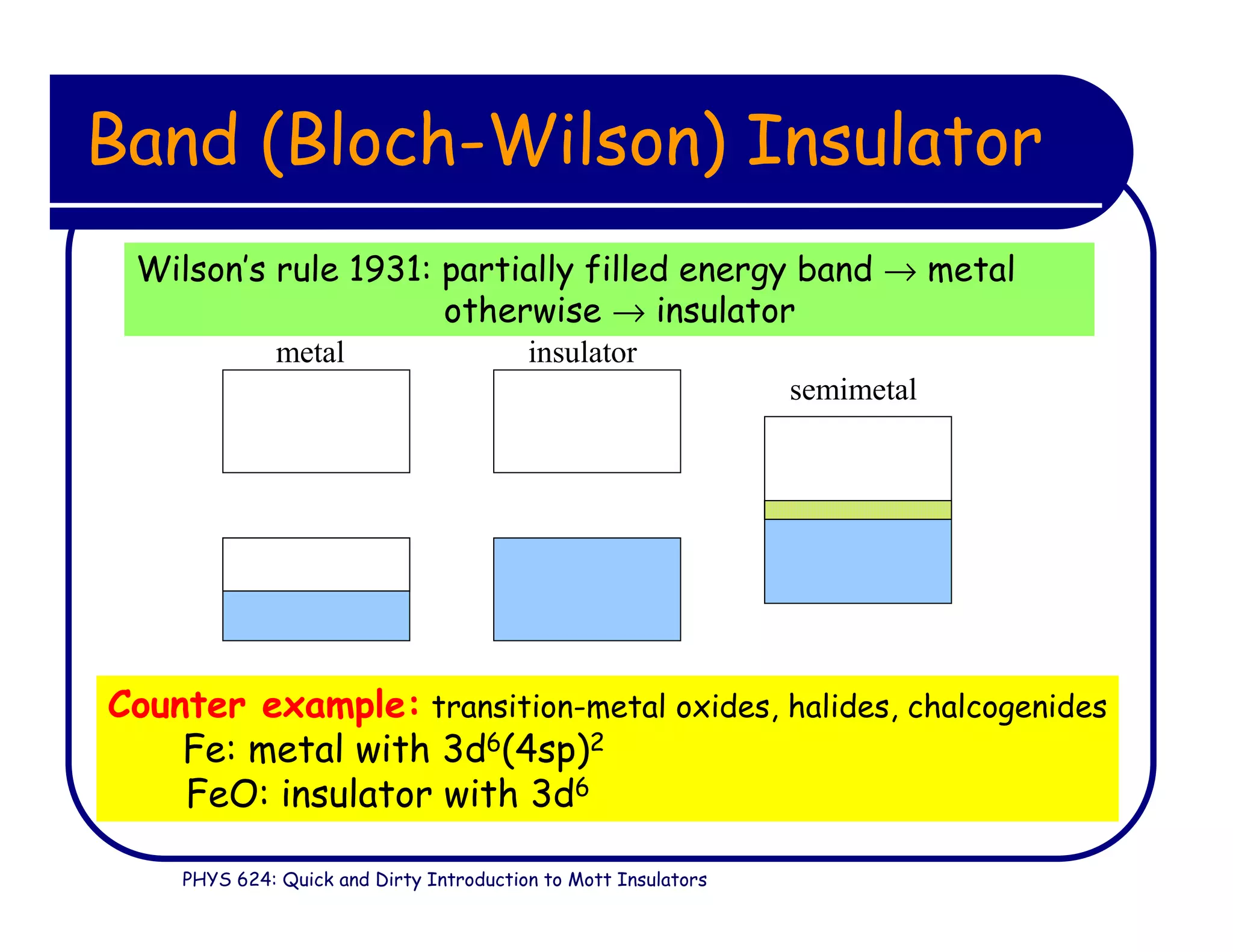
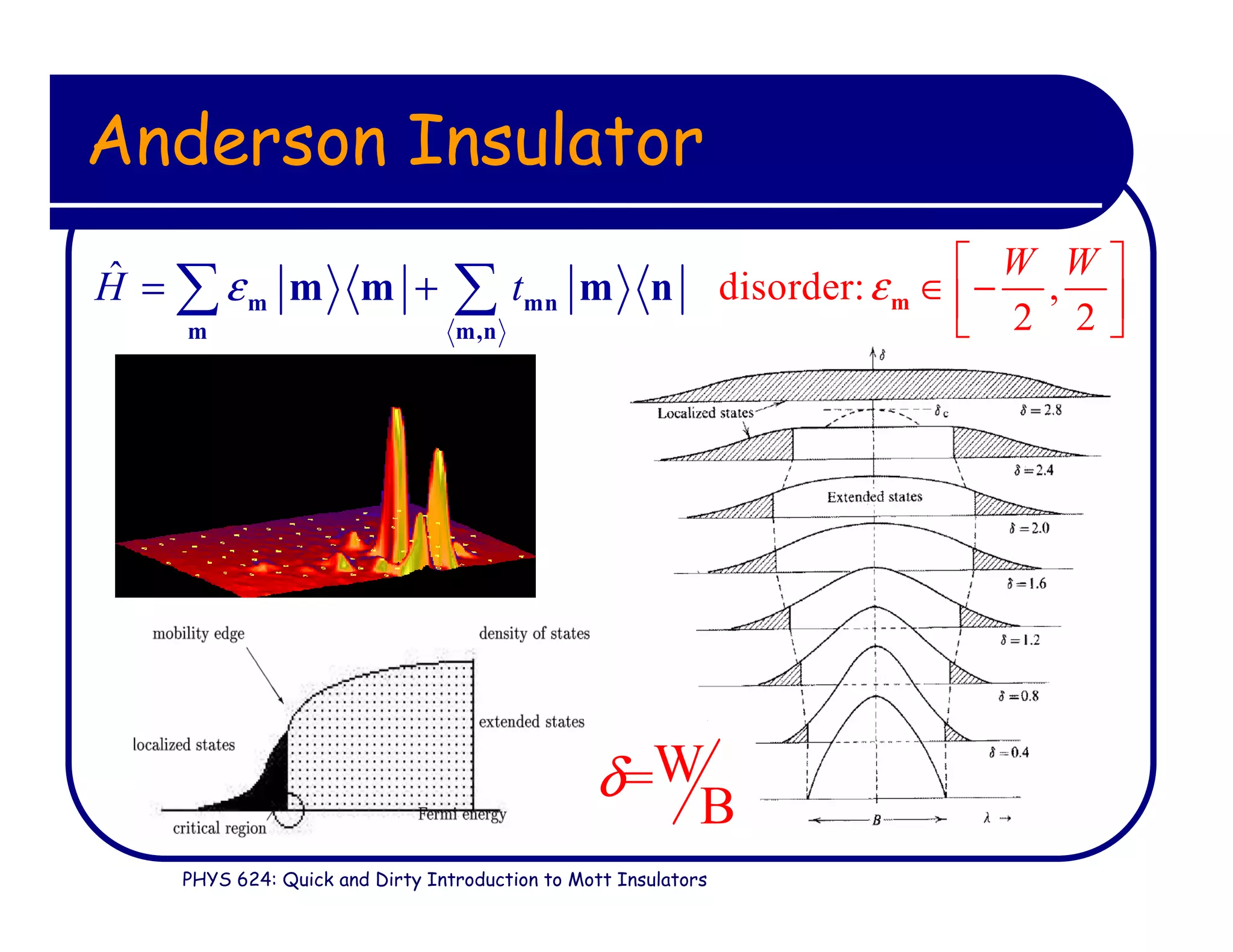
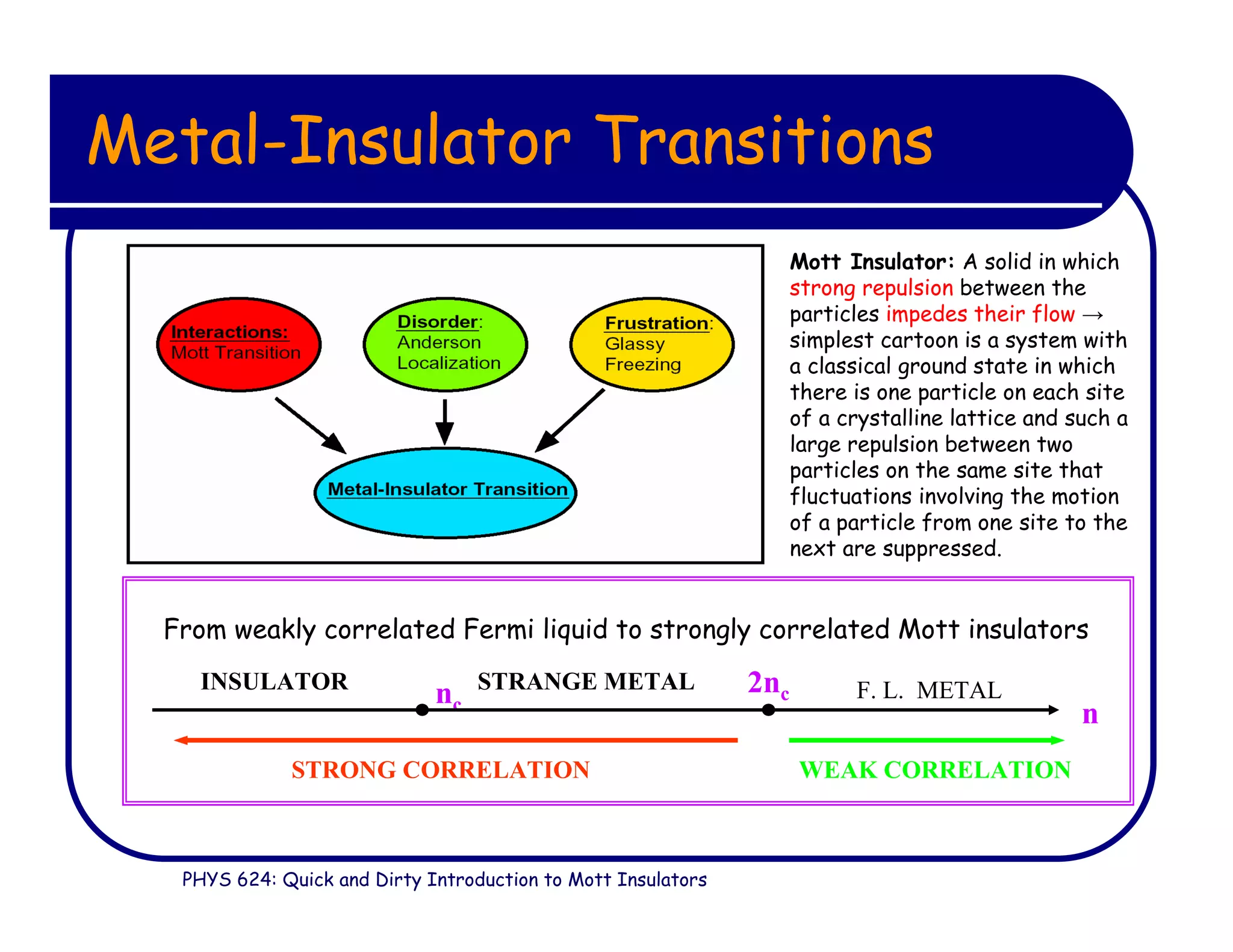
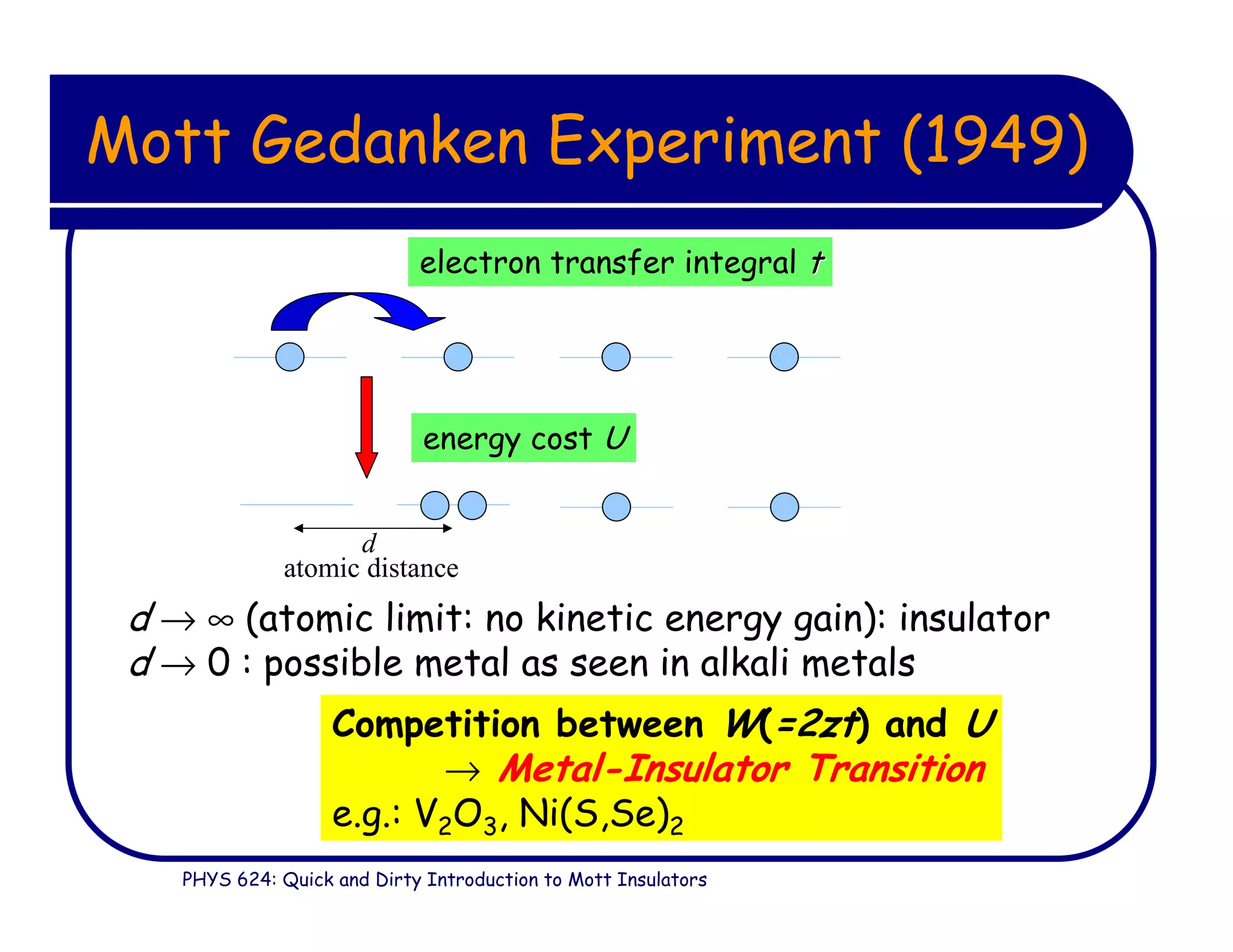
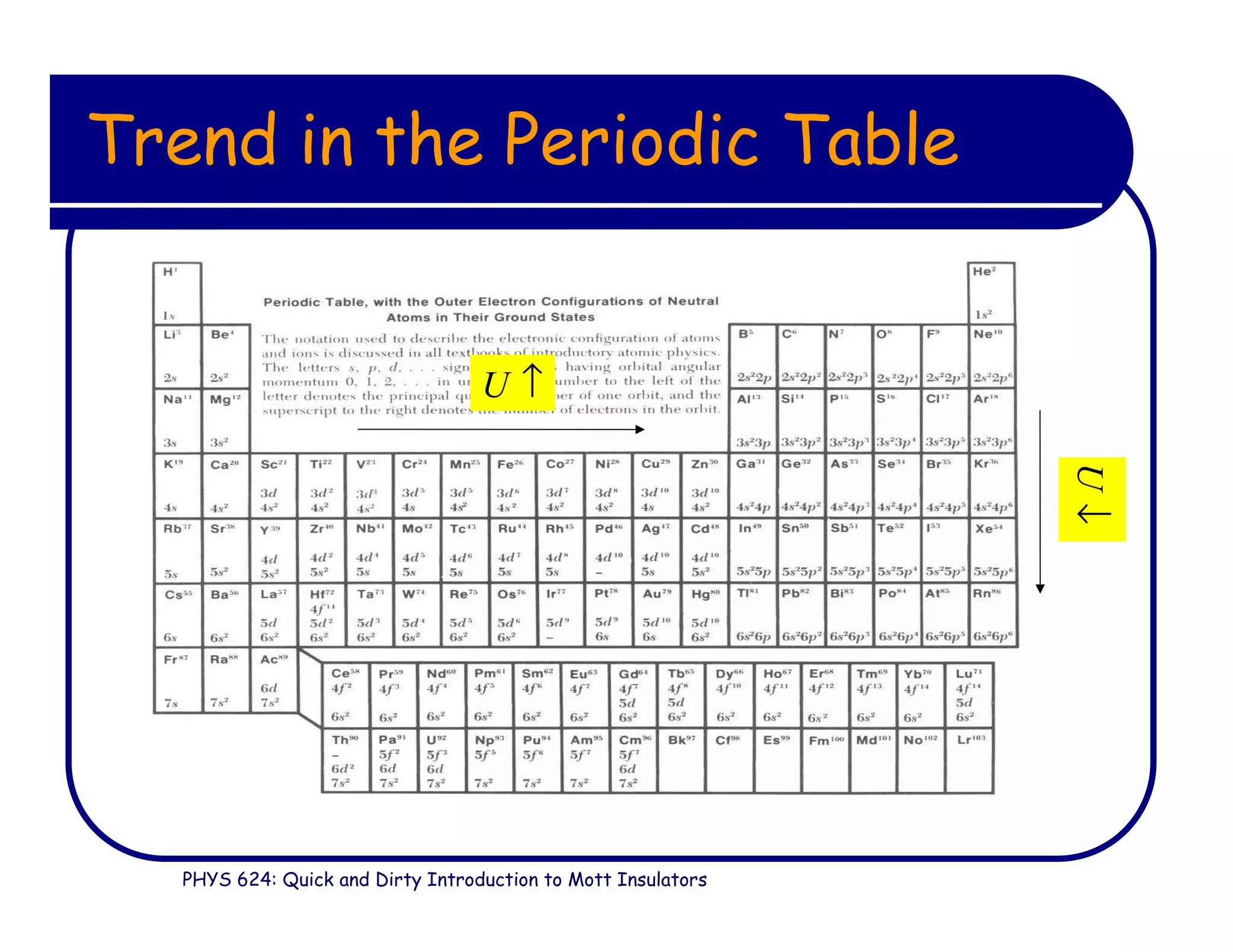
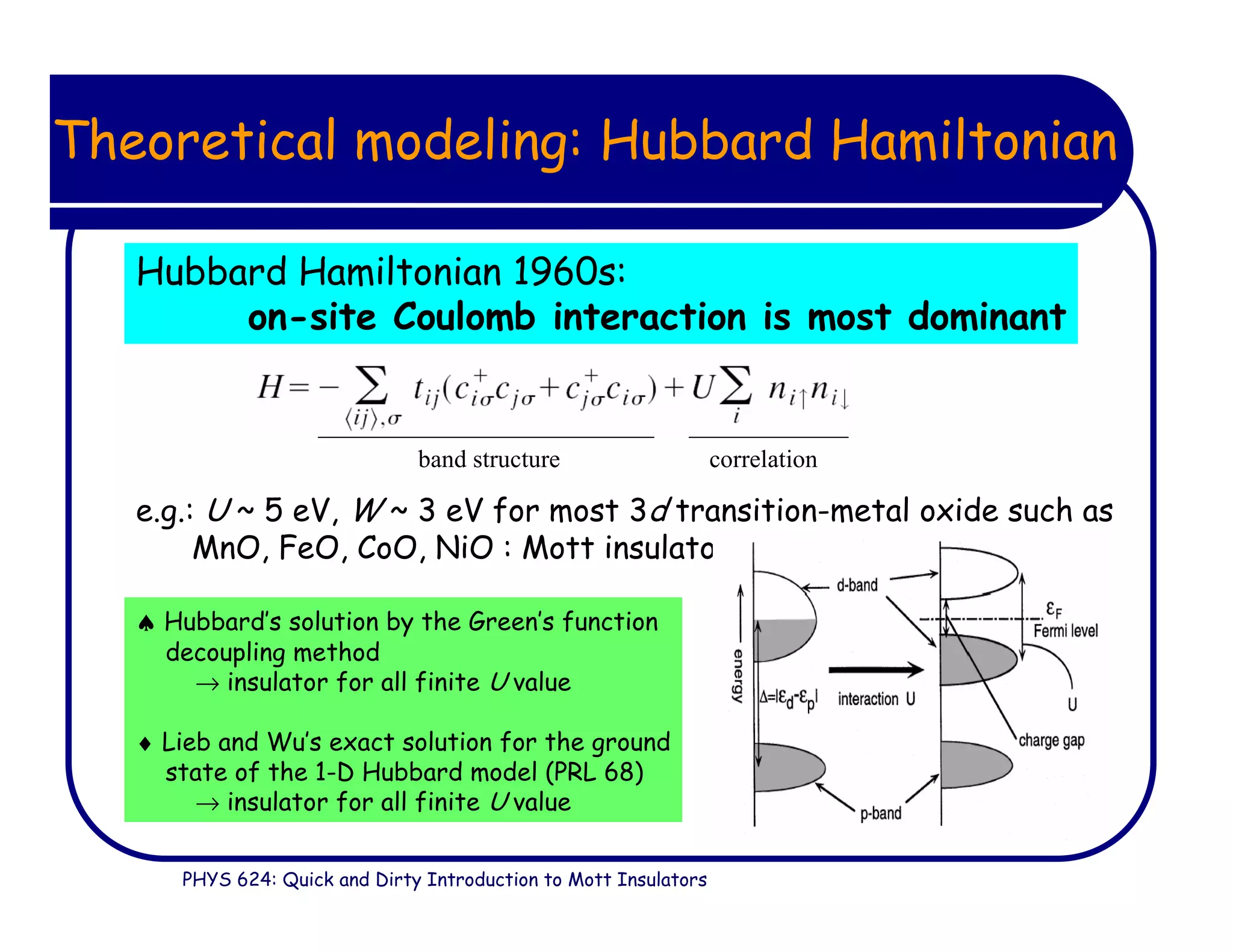
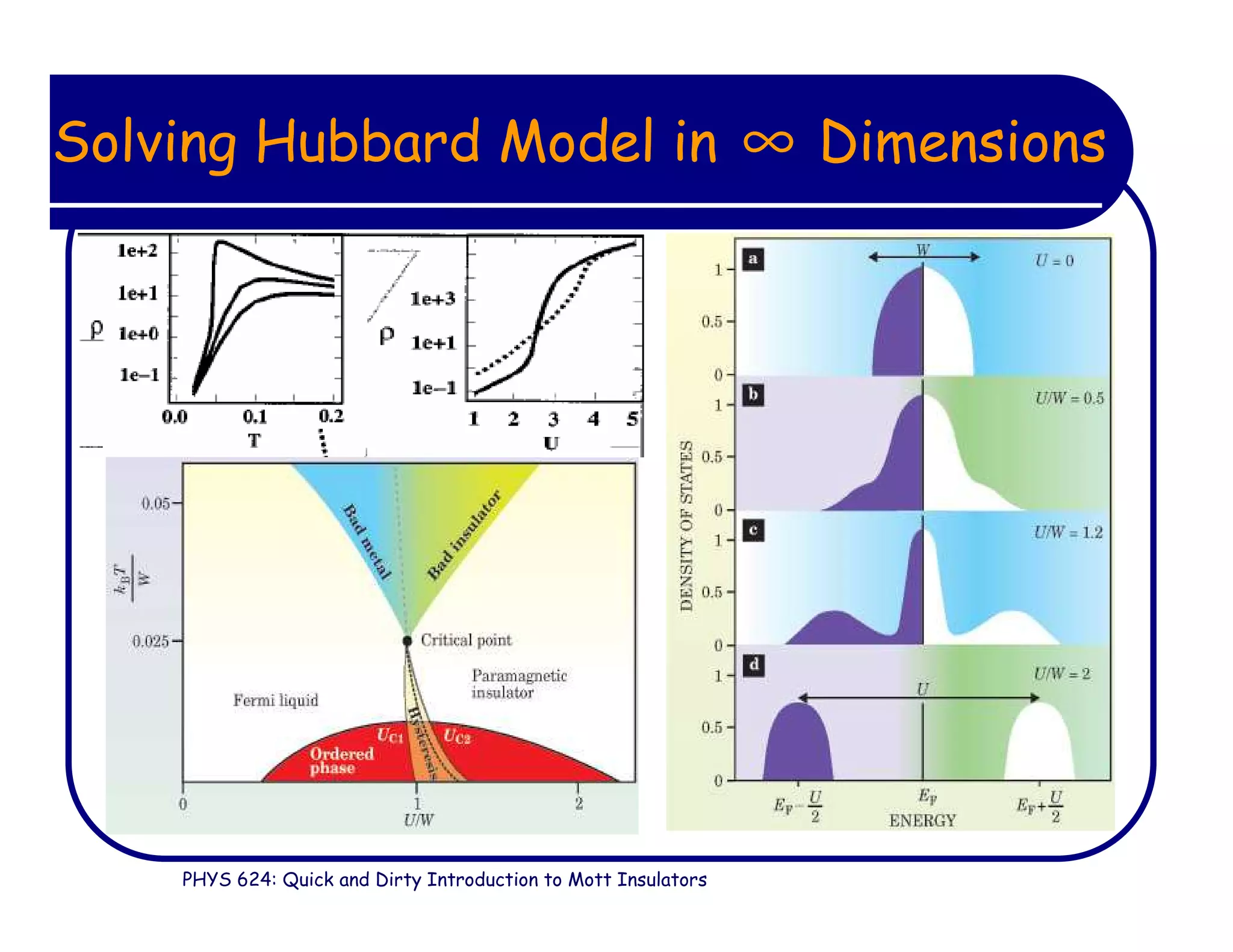
This document provides an introduction to Mott insulators, discussing their characteristics and the mechanisms behind the metal-insulator transition. It contrasts weakly correlated electron behavior with strongly correlated systems and touches upon various theoretical frameworks, such as the Hubbard model and dynamical mean-field theory. Additionally, it highlights examples, experimental observations, and the implications of these materials in solid state physics.
More Related Content
Similar to Quick and Dirty Introduction to Mott Insulators
Quick and Dirty Introduction to Mott Insulators
- 1. Quick and DirtyIntroduction to Mott Insulators Branislav K. Nikolić Department of Physics and Astronomy, University of Delaware, U.S.A. PHYS 624: Introduction to Solid State Physics http://www.physics.udel.edu/~bnikolic/teaching/phys624/phys624.html
- 2. PHYS 624: Quickand Dirty Introduction to Mott Insulators Weakly correlated electron liquid: Coulomb interaction effects ( ) ( ) ( )Fn eD Uδ ε δ=r r assume: ( ) ( , 0) ( ) F F e U f T δ ε ε θ ε ε→ = − r ≪ When local perturbation potential is switched on, some electrons will leave this region in order to ensure constant (chemical potential is a thermodynamic potential; therefore, in equilibrium it must be homogeneous throughout the crystal). ( )Uδ r Fε µ≃
- 3. PHYS 624: Quickand Dirty Introduction to Mott Insulators Thomas –Fermi Screening Except in the immediate vicinity of the perturbation charge, assume that is caused by the induced space charge → Poisson equation: 2 0 ( ) ( ) e n U δ δ ε ∇ = − r r / 2 2 2 0 2 0 1 ( ) ( ) in vacuum: ( ) 0, ( ) 4 TFr r TF F F e r U r r r r r e D q D U α δ ε ε ε δ α πε − ∂ ∂ ∇ = ⇒ = ∂ ∂ = = = = r r ( ) ( ) ( ) 2 1/3 2/3 2/3 1/32 2 2 2 2 2 0 3 1 2 4 ( ) 3 , 3 3 2 2 2 F F TF F n m n D n n r m a ε π ε π π ε π π − = = = ⇒ = ℏ ℏ 1/6 2 0 03 2 0 23 3 41 , 2 8.5 10 , 0.55Å TF Cu Cu TF n r a a me n cm r π ε − − = = ⋅ = ℏ ≃ ( )Uδ r
- 4. PHYS 624: Quickand Dirty Introduction to Mott Insulators Mott Metal-Insulator Transition Below the critical electron concentration, the potential well of the screened field extends far enough for a bound state to be formed → screening length increases so that free electrons become localized → Mott Insulators Examples: transition metal oxides, glasses, amorphous semiconductors 2 20 01/3 1/3 0 1 4 4 TF a r a n n a− ≃ ≫ ≫
- 5. PHYS 624: Quickand Dirty Introduction to Mott Insulators Metal vs. Insulator: Theory 0 0 | | 0 lim lim lim R e ( , ) 0 T αβ ω σ ω → → → = q q Theoretical Definition of an Insulator: Theoretical Definition of a Metal: Ohm law : ( , ) ( , ) ( , )j Eα αβ β β ω σ ω ω= ∑q q q ( ) 2 2 Re ( 0, 0) (1 ) cT Dαβ αβ τ σ ω π ω τ = → = + ( ) ( ) 2 1 * Drude: , Re ( 0, 0, 0) ( )c c ne D T D m αβ αβαβ αβ π δ σ ω τ δ ω− = = → → =
- 6. PHYS 624: Quickand Dirty Introduction to Mott Insulators Metal vs. Insulator: Experiment T ρ T ρ Fundamental requirements for electron transport in Fermi systems: 1) Quantum-mechanical states for electron-hole excitations must be available at energies immediately above the ground state (no gap!) since the external field provides vanishingly small energy. 2) These excitations must describe delocalized charges (no wave function localization!) that can contribute to transport over the macroscopic sample sizes.
- 7. PHYS 624: Quickand Dirty Introduction to Mott Insulators Single-Particle vs. Many-Body Insulators Insulators due to electron-ion interaction (single-particle physics): Band Insulators (electron interacts with a periodic potential of the ions → gap in the single particle spectrum) Peierls Insulators (electron interacts with static lattice deformations → gap) Anderson Insulators (electron interacts with the disorder=such as impurities and lattice imperfections) Mott Insulators due to electron-electron interaction (many-body physics leads to the gap in the charge excitation spectrum): Mott-Heisenberg (antiferromagnetic order of the pre-formed local magnetic moments below Néel temperature) Mott-Hubbard (no long-range order of local magnetic moments) Mott-Anderson (disorder + correlations) Wigner Crystal (Coulomb interaction dominates at low density of charge, rs (2D)=Ee-e/EF =ns 1/2/ns=33 or rs (3D)=67, thereby localizing electrons into a Wigner lattice)
- 8. PHYS 624: Quickand Dirty Introduction to Mott Insulators Energy Band Theory Electron in a periodic potential (crystal) → energy band ( : 1-D tight-binding band) N = 1 N = 2 N = 4 N = 8 N = 16 N = ∞ EF kinetic energy gain ( ) 2 cos( )k t kaε = −
- 9. PHYS 624: Quickand Dirty Introduction to Mott Insulators Band (Bloch-Wilson) Insulator Wilson’s rule 1931: partially filled energy band → metal otherwise → insulator metal insulator semimetal Counter example: transition-metal oxides, halides, chalcogenides Fe: metal with 3d6(4sp)2 FeO: insulator with 3d6
- 10. PHYS 624: Quickand Dirty Introduction to Mott Insulators Anderson Insulator ˆH tε= +∑ ∑m mn m m,n m m m n W= B δ disorder: , 2 2 W W ε ∈ − m
- 11. PHYS 624: Quickand Dirty Introduction to Mott Insulators Metal-Insulator Transitions From weakly correlated Fermi liquid to strongly correlated Mott insulators nc 2nc n STRONG CORRELATION WEAK CORRELATION INSULATOR STRANGE METAL F. L. METAL Mott Insulator: A solid in which strong repulsion between the particles impedes their flow → simplest cartoon is a system with a classical ground state in which there is one particle on each site of a crystalline lattice and such a large repulsion between two particles on the same site that fluctuations involving the motion of a particle from one site to the next are suppressed.
- 12. PHYS 624: Quickand Dirty Introduction to Mott Insulators Mott Gedanken Experiment (1949) energy cost U electron transfer integral tt Competition between W(=2zt) and U → Metal-Insulator Transition e.g.: V2O3, Ni(S,Se)2 d atomic distance d → ∞ (atomic limit: no kinetic energy gain): insulator d → 0 : possible metal as seen in alkali metals
- 13. PHYS 624: Quickand Dirty Introduction to Mott Insulators Mott vs. Bloch-Wilson insulators Band insulator, including familiar semiconductors, is state produced by a subtle quantum interference effects which arise from the fact that electrons are fermions. Nevertheless one generally accounts band insulators to be “simple” because the band theory of solids successfully accounts for their properties. Generally speaking, states with charge gaps (including both Mott and Bloch- Wilson insulators) occur in crystalline systems at isolated “occupation numbers” where is the number of particles per unit cell. Although the physical origin of a Mott insulator is understandable to any child, other properties, especially the response to doping are only partially understood. Mott state, in addition to being insulating, can be characterized by: presence or absence of spontaneously broken symmetry (e.g., spin antiferromagnetism); gapped or gapless low energy neutral particle excitations; and presence or absence of topological order and charge fractionalization. * ν ν=* ν * ν ν δ→ −
- 14. PHYS 624: Quickand Dirty Introduction to Mott Insulators Trend in the Periodic Table U ↑ U↓
- 15. PHYS 624: Quickand Dirty Introduction to Mott Insulators Theoretical modeling: Hubbard Hamiltonian Hubbard Hamiltonian 1960s: on-site Coulomb interaction is most dominant ♠ Hubbard’s solution by the Green’s function decoupling method → insulator for all finite U value ♦ Lieb and Wu’s exact solution for the ground state of the 1-D Hubbard model (PRL 68) → insulator for all finite U value e.g.: U ~ 5 eV, W ~ 3 eV for most 3d transition-metal oxide such as MnO, FeO, CoO, NiO : Mott insulator band structure correlation
- 16. PHYS 624: Quickand Dirty Introduction to Mott Insulators Solving Hubbard Model in Dimensions∞
- 17. PHYS 624: Quickand Dirty Introduction to Mott Insulators Dynamical Mean-Field Theory in Pictures In ∞-D, spatial fluctuation can be neglected. → mean-field solution becomes exact. Hubbard model → single-impurity Anderson model in a mean-field bath. Solve exactly in the time domain → “dynamical” mean-field theory Dynamical mean-field theory (DMFT) of correlated-electron solids replaces the full lattice of atoms and electrons with a single impurity atom imagined to exist in a bath of electrons. The approximation captures the dynamics of electrons on a central atom (in orange) as it fluctuates among different atomic configurations, shown here as snapshots in time. In the simplest case of an s orbital occupying an atom, fluctuations could vary among |0〉, | ↑ 〉, | ↓ 〉, or | ↑ ↓ 〉, which refer to an unoccupied state, a state with a single electron of spin-up, one with spin- down, and a doubly occupied state with opposite spins. In this illustration of one possible sequence involving two transitions, an atom in an empty state absorbs an electron from the surrounding reservoir in each transition. The hybridization Vν is the quantum mechanical amplitude that specifies how likely a state flips between two different configurations.
- 18. PHYS 624: Quickand Dirty Introduction to Mott Insulators Static vs. Dynamic Mean-Field Theory Static = Hartree-Fock or Density Functional Theory: Dynamic = Dynamical Mean-Field Theory: 3 2 3 3 [ ( )] [ ( )] ( ) ( ) ( ) ( ) ( )1 ( ) ( ) 2[ ( )] 2 | | kinetic ext KS i exchange E V d V md d E ρ ρ ρ ερ ρ ρ Γ = + ⇒ + Ψ = Ψ′ ′+ + ′− ∫ ∫ r r r r r r r rr r r r r r r ℏ 23 [ ( )]( ) [ ( )] ( ) , ( ) ( )| ( )| | | ( ) exchange KS ext i i i E V V d f δ ρρ ρ ρ ε δρ ′ ′= + + = Ψ ′− ∑∫ rr r r r r r r r r [ ] 3 1 3 3 [ ( ), ] [ ( ), ] ( ) ( ) [ ( )] [ ( )] 1 ( ) ( ) [ ( ), ] [ ( )] ( ) 1/ [ ( )]2 | | kinetic ext exchange G E G V d G t d d E G G ρ ρ ρ ω ω ω ρ ρ ρ ω ω ω ω −Γ = + ∆ = − Σ ∆ − ⇒ ′ ′+ + Σ ∆ ≡ ∆ − ∆ +′− ∫ ∑ ∫ k k r r r r r r r r r r r r
- 19. PHYS 624: Quickand Dirty Introduction to Mott Insulators Transition from non-Fermi Liquid Metal to Mott Insulator Model: Mobile spin- ↑ electrons interact with frozen spin- ↓ electrons. NOTE: DOS well-defined even though there are no fermionic quasiparticles.
- 20. PHYS 624: Quickand Dirty Introduction to Mott Insulators Experiment: Photoemission Spectroscopy hν (K,λ) > W e- (Ek,k,σσσσ) N-particle (N−1)-particle P(| i 〉 → | f 〉) Sudden approximation Einstein’s photoelectric effect Photoemission current is given by: Ei N Ef N −1 ∑ −+><= −− − fi N i N fr TkE EEiTfe Z A B N i , 12/ )(|| 1 )( ωδω
- 21. PHYS 624: Quickand Dirty Introduction to Mott Insulators Mott Insulating Material: V2O3 → a = 4.95 Å → c = 14.0 Å – (1012) cleavage plane Vanadium Oxygen surface-layer thickness = side view 2.44Å top view
- 22. PHYS 624: Quickand Dirty Introduction to Mott Insulators Theory vs. Experiment: Photoemission Spectroscopy Photoemission spectrum of metallic vanadium oxide V2O3 near the metal−insulator transition. The dynamical mean-field theory calculation (solid curve) mimics the qualitative features of the experimental spectra. The theory resolves the sharp quasiparticle band adjacent to the Fermi level and the occupied Hubbard band, which accounts for the effect of localized d electrons in the lattice. Higher-energy photons (used to create the blue spectrum) are less surface sensitive and can better resolve the quasiparticle peak. Phys. Rev. Lett. 90, 186403 (2003)
- 23. PHYS 624: Quickand Dirty Introduction to Mott Insulators Phase Diagram of V2O3
- 24. PHYS 624: Quickand Dirty Introduction to Mott Insulators Wigner Crystal Since the mid-1930s, theorists have predicted the crystallization of electrons. If a small number of electrons are restricted to a plane, put into a liquid-like state, and squeezed, they arrange themselves into the lowest energy configuration possible--a series of concentric rings. Each electron inhabits only a small region of a ring, and this bull's-eye pattern is called a Wigner crystal. Only a handful of difficult experiments have shown indirect evidence of this phenomenon → Electrons trapped on a free surface of liquid helium offer an excellent high mobility 2D electron system. Since the free surface of liquid He is extremely smooth, the mobility of electrons increases enormously at low temperatures.
- 25. PHYS 624: Quickand Dirty Introduction to Mott Insulators Beyond Solid State Physics: Bosonic Mott Insulators in Optical Lattices EVOLUTION: Superfluid state with coherence, Mott Insulator without coherence, and superfluid state after restoring the coherence.