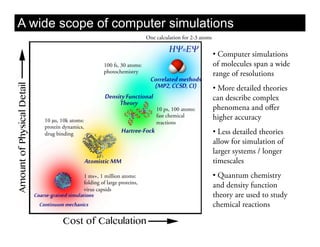
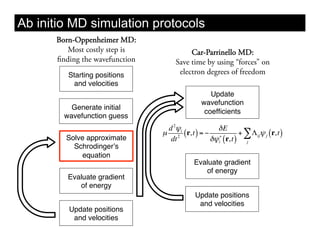
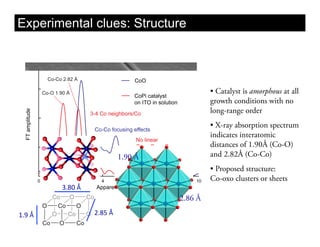
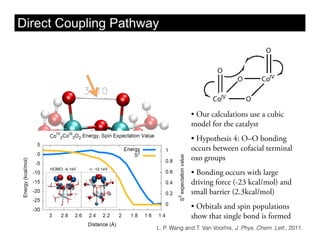
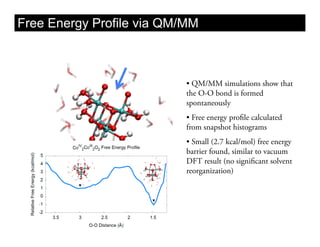
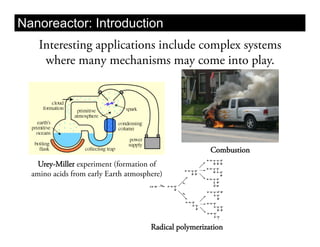
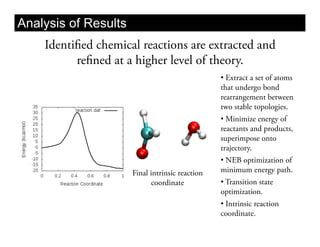
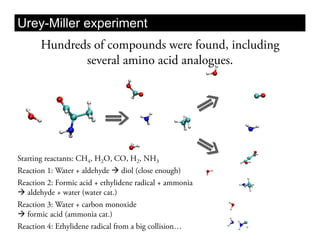
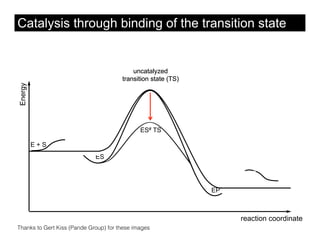
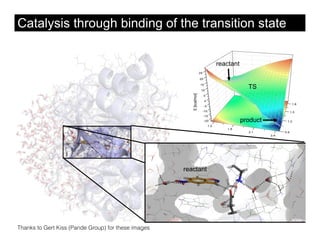
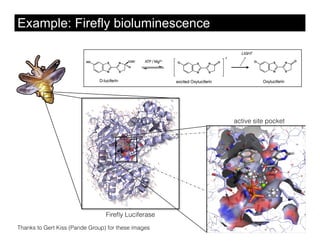
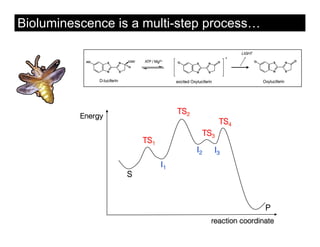
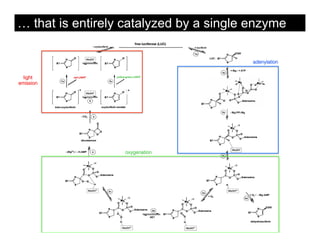
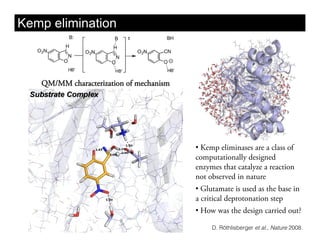
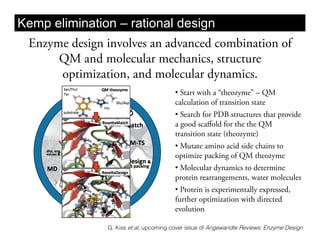
This document discusses ab initio molecular dynamics simulation methods. It provides an overview of different simulation techniques that range from fully quantum to mixed quantum-classical approaches. These methods allow researchers to study molecular phenomena with varying degrees of accuracy and system sizes. The document also outlines key concepts like the Schrodinger equation and Born-Oppenheimer approximation that are fundamental to these simulation approaches.

1. Ab initio molecular
dynamics"
Lee-Ping Wang"
leeping @ stanford.edu "
March 4, 2013"

2. Outline
Review
• A wide range of simulation methods
• Schrödinger’s equation and the potential energy surface
Methods
• Molecular forces and the Hellmann-Feynman theorem
• Born-Oppenheimer and Car-Parrinello molecular dynamics
• Hybrid quantum/classical methods
Applications
• O-O bonding mechanism of cobalt water oxidation catalyst
• Simulating the Urey-Miller experiment
• Enzyme catalysis and rational enzyme design

3. A wide scope of computer simulations
One calculation for 2-3 atoms
• Computer simulations
100 fs, 30 atoms: of molecules span a wide
photochemistry range of resolutions
• More detailed theories
can describe complex
10 ps, 100 atoms: phenomena and offer
fast chemical higher accuracy
10 µs, 10k atoms: reactions
protein dynamics,
drug binding • Less detailed theories
allow for simulation of
larger systems / longer
timescales
1 ms+, 1 million atoms: • Quantum chemistry
folding of large proteins,
virus capsids
and density function
theory are used to study
chemical reactions

4. Categories of simulations
Focus on the physics rather than the nomenclature.
• Quantum treatment of electrons or force field?
QM: ab initio molecular dynamics (note: nuclei may be classical)
Force field: classical MD or molecular mechanics
• Born-Oppenheimer approximation broken or excited states?
Nonadiabatic dynamics, excited state dynamics
• Quantum treatment of nuclei?
Quantum dynamics, path integral MD

5. The Schrödinger equation
All ground-state quantum chemistry is based on the
time-independent Schrödinger’s equation.
ˆ
ΗΨ = EΨ
(T + V ) Ψ = EΨ
ˆ ˆ
% "2 (
' !# i + # Z I Z J ! # Z I + # 1 * + ( ri ;R I ) = E ( R I ) + ( ri ;R I )
' ˆ ˆ ˆ *
& i 2 I$J R I ! R iJ i,I R I ! ri i$ j ri ! rj )
Kinetic Nuclear Electron Electron
energy repulsion nuclear electron Electron Electronic
operator (just a “number”) attraction repulsion wavefunction energy
Born-Oppenheimer approximation:
when solving for the electronic
wavefunction, treat nuclei as static
external potentials

6. Introduction: Molecular dynamics simulation
e fundamental equation of classical molecular
dynamics is Newton’s second law.
Key approximations:
e force is given by the negative gradient of the • Born-Oppenheimer
potential energy. approximation; no
transitions between
dE
F=! electronic states
dR • Approximate potential
Knowing the force allows us to accelerate the atoms in energy surface, either
the direction of the force. from quantum chemistry
or from the force field
F = ma • Classical mechanics!
Nuclei are quantum
particles in reality, but
this is ignored.

7. Outline
Review
• A wide range of simulation methods
• Schrödinger’s equation and the potential energy surface
Methods
• Molecular forces and the Hellmann-Feynman theorem
• Born-Oppenheimer and Car-Parrinello molecular dynamics
• Hybrid quantum/classical methods
Applications
• O-O bonding mechanism of cobalt water oxidation catalyst
• Simulating the Urey-Miller experiment
• Enzyme catalysis; mechanistic investigation and rational design

8. Hellmann-Feynman theorem
e Hellmann-Feynman dH
dE !
ˆ
theorem makes the
dR dR
"
calculation of molecular forces! ( r )
= dr! ( r) (r) possible.
ˆ
H ! ( r) = E! ( r); "
! dr! (r)! (r) = 1 ˆ
H ! =E ! ; ! ! =1
! dr! " ˆ " "
(r) H! (r) = ! ! E! = E ! ! ! = E ˆ
! H ! = ! E ! =E ! ! =E
dE d ˆ dE d ˆ
=
dR dR
" dr! ! (r)H! (r) =
dR dR
!H!
d! ! ˆ ˆ d! ˆ ˆ
dH
=" H! + ! ! dH ˆ d!
! + ! !H = H! + ! ˆ d!
! + !H
dR dR dR dR dR dR
d! ! ! dH
ˆ d! dHˆ d! d!
=" E! + ! ! + ! !E = ! ! + E! + ! E
dR dR dR dR dR dR
" d! ! d! % ˆ
dH ˆ
dH d! d!
= ( E$ ! + !! ' + !! ! = ! ! +E ! +E !
# dR dR & dR dR dR dR
d ! dH
ˆ ˆ
dH d
="E
dR
(! ! ) + ! dR !
!
= !
dR
! +E
dR
!!
d dH ˆ dHˆ dHˆ d ˆ
dH
=E 1+ " ! ! ! = " !! ! = ! ! +E 1 = ! !
dR dR dR dR dR dR

9. Ab initio MD simulation protocols
Born-Oppenheimer MD:
Most costly step is Car-Parrinello MD:
finding the wavefunction Save time by using “forces” on
Starting positions electron degrees of freedom
and velocities"
Update
wavefunction
Generate initial
coefficients"
wavefunction guess"
d 2!i !E
µ 2 ( r, t ) = ! " + $ # ij! j ( r, t )
Solve approximate dt !"i ( r, t ) j
Schrodingerʼs
equation"
Evaluate gradient
of energy"
Evaluate gradient
of energy"
Update positions
and velocities"
Update positions
and velocities"

10. Hybrid quantum / classical methods
Hybrid methods allow us to simulate different parts
of a system using different levels of theory.
• Many interesting problems contain quantum behavior but are too
large for quantum methods
• However, QM behavior is often confined to a small part of the system
• A simple approximation: Run QM only where exciting stuff happens
ONIOM = MM (Entire system) + QM (Selection) – MM (Selection)
ONIOM does not explicitly contain interactions between QM and MM subsystems
S. Dapprich and coworkers, JMS Theochem (1999), 462, 1.

11. QM/MM Framework
In QM/MM, the QM and MM subsystems interact
via the QM/MM Hamiltonian.
ETotal = EQM ( rQM ) + EMM ( rMM ) + EQM/MM ( rQM , rMM )
If the two subsystems are independent (i.e. wavefunction is close to an
antisymmetric product), then the QM/MM Hamiltonian is simple:
MM Nuclei / QM Nuclei! MM Electrons / QM Nuclei!
MM Nuclei / QM Electrons!
QM Electrons / MM Electrons!
Now approximate:
MM Nuclei+Electrons = partial charges !
P. Slavicek and T. J. Martinez, J. Chem. Phys. (2006), 124, 084107.

12. QM/MM Framework
From the QM system’s perspective,
the MM system looks like a bunch of point charges.
Neglected effects:
• Exchange antisymmetry, dispersion (still need an
empirical vdW interaction between QM and MM atoms)
• Covalent bonds (leads to the link atom problem)
P. Slavicek and T. J. Martinez, J. Chem. Phys. (2006), 124, 084107.

13. Outline
Review
• A wide range of simulation methods
• Schrödinger’s equation and the potential energy surface
Methods
• Molecular forces and the Hellmann-Feynman theorem
• Born-Oppenheimer and Car-Parrinello molecular dynamics
• Hybrid quantum/classical methods
Applications
• O-O bonding mechanism of cobalt water oxidation catalyst
• Simulating the Urey-Miller experiment
• Enzyme catalysis and rational enzyme design

14. Cobalt water oxidation catalyst
• Catalyst electrodeposits
in solution of Co2+ and
phosphate buffer (Pi)
• Rapid water oxidation
catalysis at mild
overpotential
• Catalyst is self-healing;
does not corrode, catalysis
rate continues to increase
Image courtesy Y. Surendranath
Kanan and Nocera, Science (2008).

15. Experimental clues: Structure
• Catalyst is amorphous at all
growth conditions with no
long-range order
• X-ray absorption spectrum
indicates interatomic
distances of 1.90Å (Co-O)
1.90 Å and 2.82Å (Co-Co)
• Proposed structure:
Co-oxo clusters or sheets
3.80
Å
2.86 Å
1.9
Å
2.85
Å

16. Direct Coupling Pathway
• Our calculations use a cubic
model for the catalyst
• Hypothesis 4: O–O bonding
occurs between cofacial terminal
oxo groups
• Bonding occurs with large
driving force (-23 kcal/mol) and
small barrier (2.3kcal/mol)
• Orbitals and spin populations
show that single bond is formed
L. P. Wang and T. Van Voorhis, J. Phys. Chem. Lett., 2011.

17. Free Energy Profile via QM/MM
• QM/MM simulations show that
the O-O bond is formed
spontaneously
• Free energy profile calculated
from snapshot histograms
• Small (2.7 kcal/mol) free energy
barrier found, similar to vacuum
DFT result (no significant solvent
reorganization)

18. Outline
Review
• A wide range of simulation methods
• Schrödinger’s equation and the potential energy surface
Methods
• Molecular forces and the Hellmann-Feynman theorem
• Born-Oppenheimer and Car-Parrinello molecular dynamics
• Hybrid quantum/classical methods
Applications
• O-O bonding mechanism of cobalt water oxidation catalyst
• Simulating the Urey-Miller experiment
• Enzyme catalysis and rational enzyme design

19. Nanoreactor: Introduction
Interesting applications include complex systems
where many mechanisms may come into play.
Combustion
Urey-Miller experiment (formation of
amino acids from early Earth atmosphere)
Radical polymerization

20. Early work
• GPU-accelerated quantum
chemistry is potentially useful for
long timescale (~1 ns) reactive
molecular dynamics.
• Need improved analysis tools to
extract knowledge from simulations.
Early analysis of a very simple
AIMD trajectory (HF / 3-21G, 120
atoms, 1500 K, 27 ps)
Red = Transient species
Gray = Hydrogen
Blue = Acetylene
Gold = Ethane
Violet = Ethylene
Green = Vinylidene radical

21. Time-dependent spherical boundary condition
e square-wave spherical boundary condition leads
to high-velocity molecular collisions.
• Kinetic energy momentarily
reaches equivalent of 6000-10000K
• Equivalent pressure to compress an
ideal gas is 10 kbar (bottom of
Earth’s crust)
• Analogous conditions in the real
world: Meteorite impacts?

22. Analysis of Results
Identified chemical reactions are extracted and
refined at a higher level of theory.
• Extract a set of atoms
that undergo bond
rearrangement between
two stable topologies.
• Minimize energy of
reactants and products,
superimpose onto
trajectory.
• NEB optimization of
Raw data from MD trajectory Final intrinsic reaction minimum energy path.
coordinate • Transition state
optimization.
• Intrinsic reaction
coordinate.

23. Urey-Miller experiment
Hundreds of compounds were found, including
several amino acid analogues.
Starting reactants: CH4, H2O, CO, H2, NH3
Reaction 1: Water + aldehyde à diol (close enough)
Reaction 2: Formic acid + ethylidene radical + ammonia
à aldehyde + water (water cat.)
Reaction 3: Water + carbon monoxide
à formic acid (ammonia cat.)
Reaction 4: Ethylidene radical from a big collision…

24. Outline
Review
• A wide range of simulation methods
• Schrödinger’s equation and the potential energy surface
Methods
• Molecular forces and the Hellmann-Feynman theorem
• Born-Oppenheimer and Car-Parrinello molecular dynamics
• Hybrid quantum/classical methods
Applications
• O-O bonding mechanism of cobalt water oxidation catalyst
• Simulating the Urey-Miller experiment
• Enzyme catalysis and rational enzyme design

25. Catalysis through binding of the transition state
uncatalyzed
transition state (TS)
Energy
ES# TS
E+S
ES
EP
reaction coordinate
Thanks to Gert Kiss (Pande Group) for these images

26. Catalysis through binding of the transition state
reactant
TS
product
reactant
Thanks to Gert Kiss (Pande Group) for these images

27. Example: Firefly bioluminescence
LIGHT
*
HO COO- ATP / Mg2+ -
O O
-
O S N
O
S N S N
H
N S N S N S
D-luciferin excited Oxyluciferin Oxyluciferin
active site pocket
Firefly Luciferase
Thanks to Gert Kiss (Pande Group) for these images

28. Bioluminescence is a multi-step process…
LIGHT
*
HO COO- ATP / Mg2+ -
O O
-
O S N
O
S N S N
H
N S N S N S
D-luciferin excited Oxyluciferin Oxyluciferin
TS2
Energy
TS4
TS3
TS1
I2 I3
I1
S
P
reaction coordinate

29. … that is entirely catalyzed by a single enzyme
adenylation
light
emission
oxygenation

30. Kemp elimination
QM/MM characterization of mechanism
• Kemp eliminases are a class of
computationally designed
enzymes that catalyze a reaction
not observed in nature
• Glutamate is used as the base in
a critical deprotonation step
• How was the design carried out?
D. Röthlisberger et al., Nature 2008.

31. Kemp elimination – rational design
Enzyme design involves an advanced combination of
QM and molecular mechanics, structure
optimization, and molecular dynamics.
• Start with a “theozyme” – QM
calculation of transition state
• Search for PDB structures that provide
a good scaffold for the the QM
transition state (theozyme)
• Mutate amino acid side chains to
optimize packing of QM theozyme
• Molecular dynamics to determine
protein rearrangements, water molecules
• Protein is experimentally expressed,
further optimization with directed
evolution
G. Kiss et al, upcoming cover issue of Angewandte Reviews: Enzyme Design