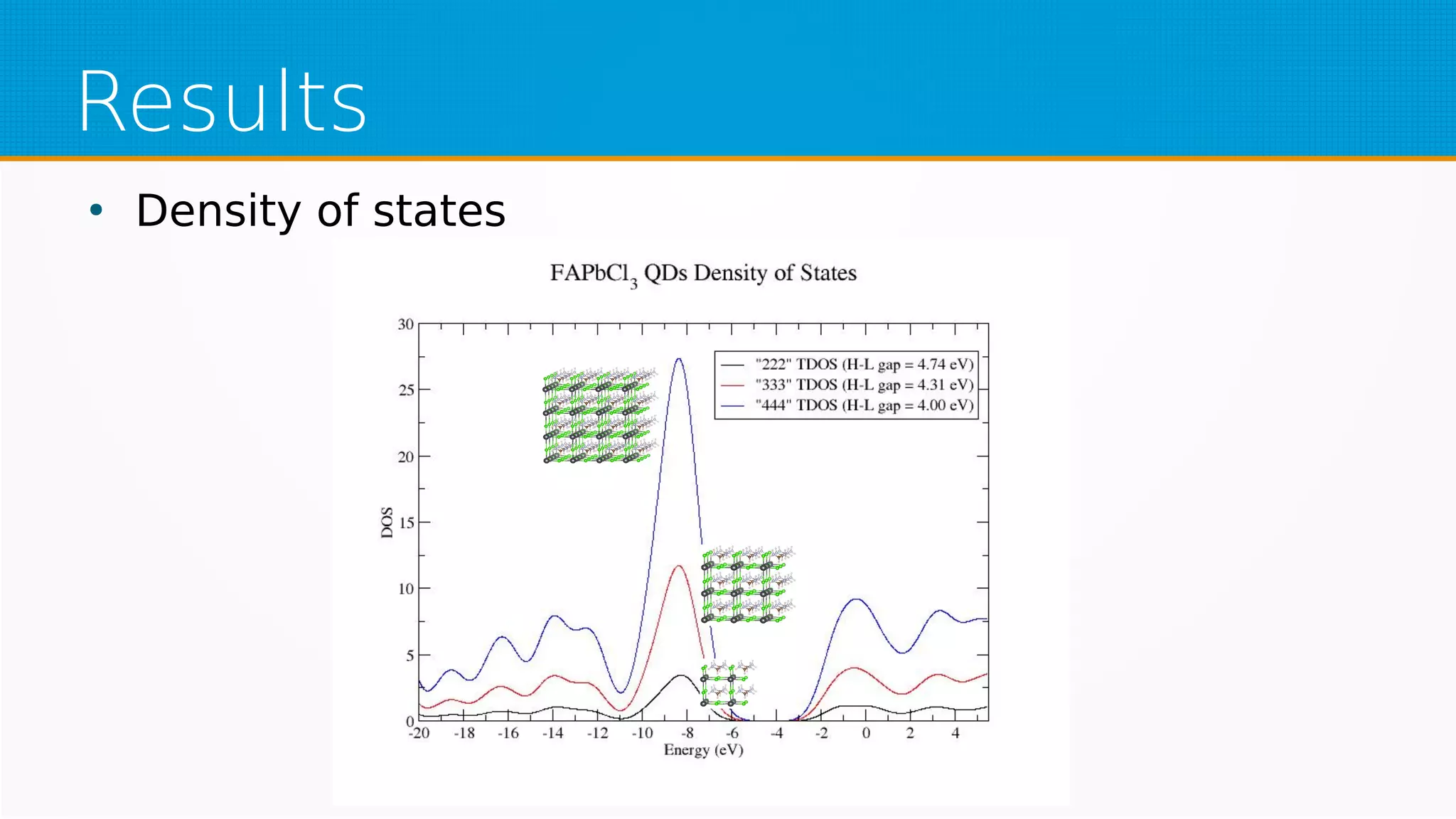
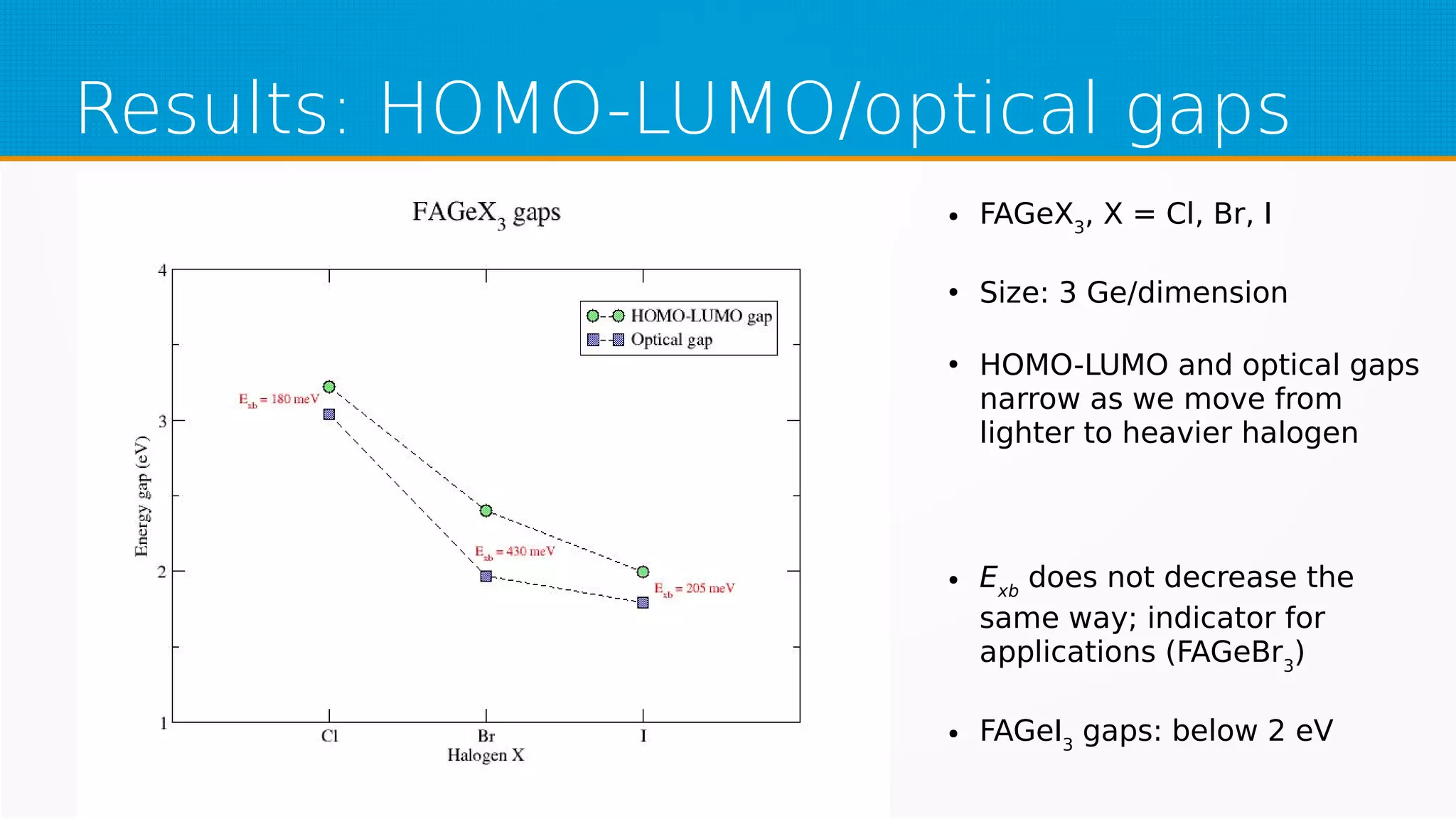
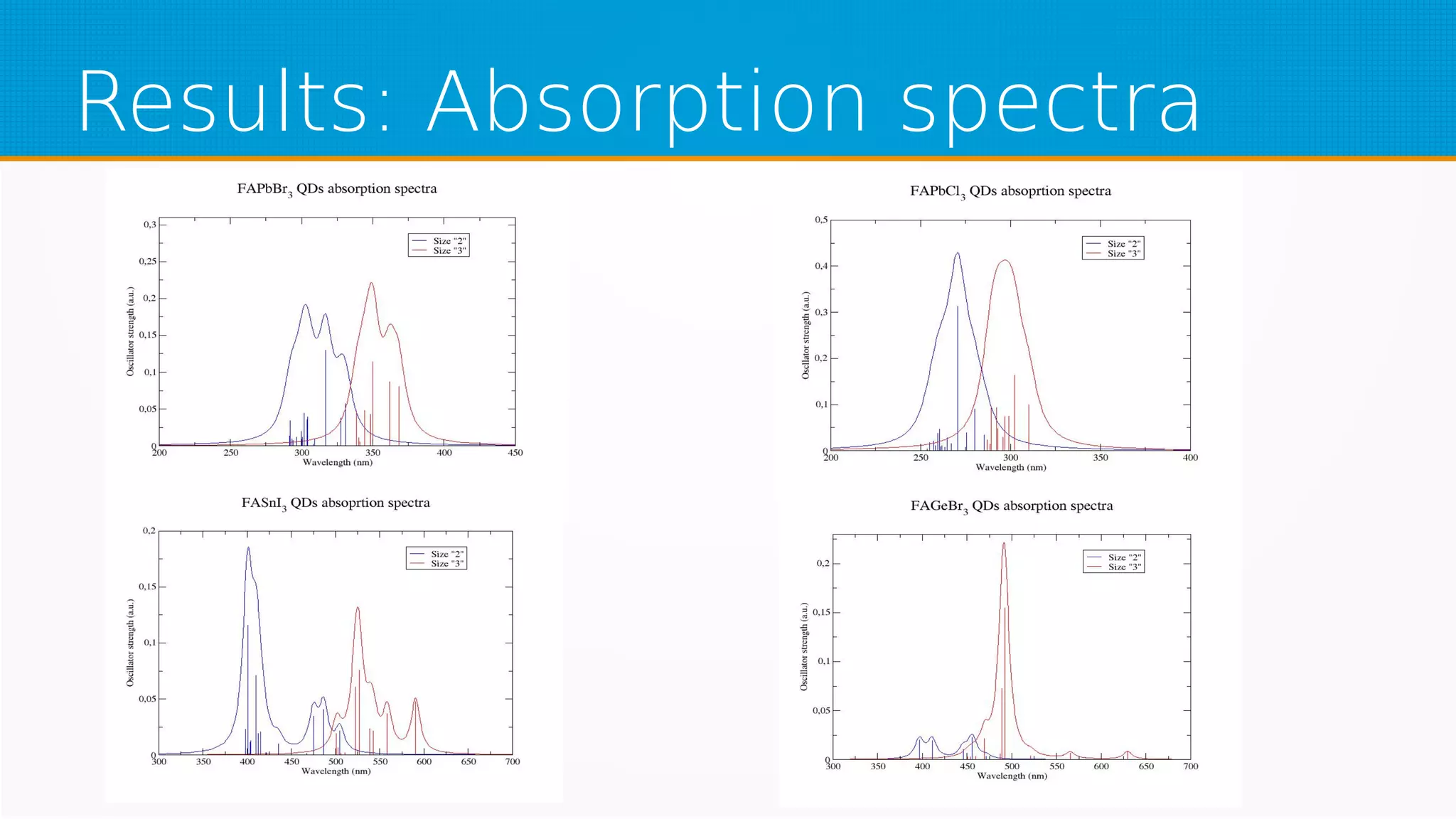
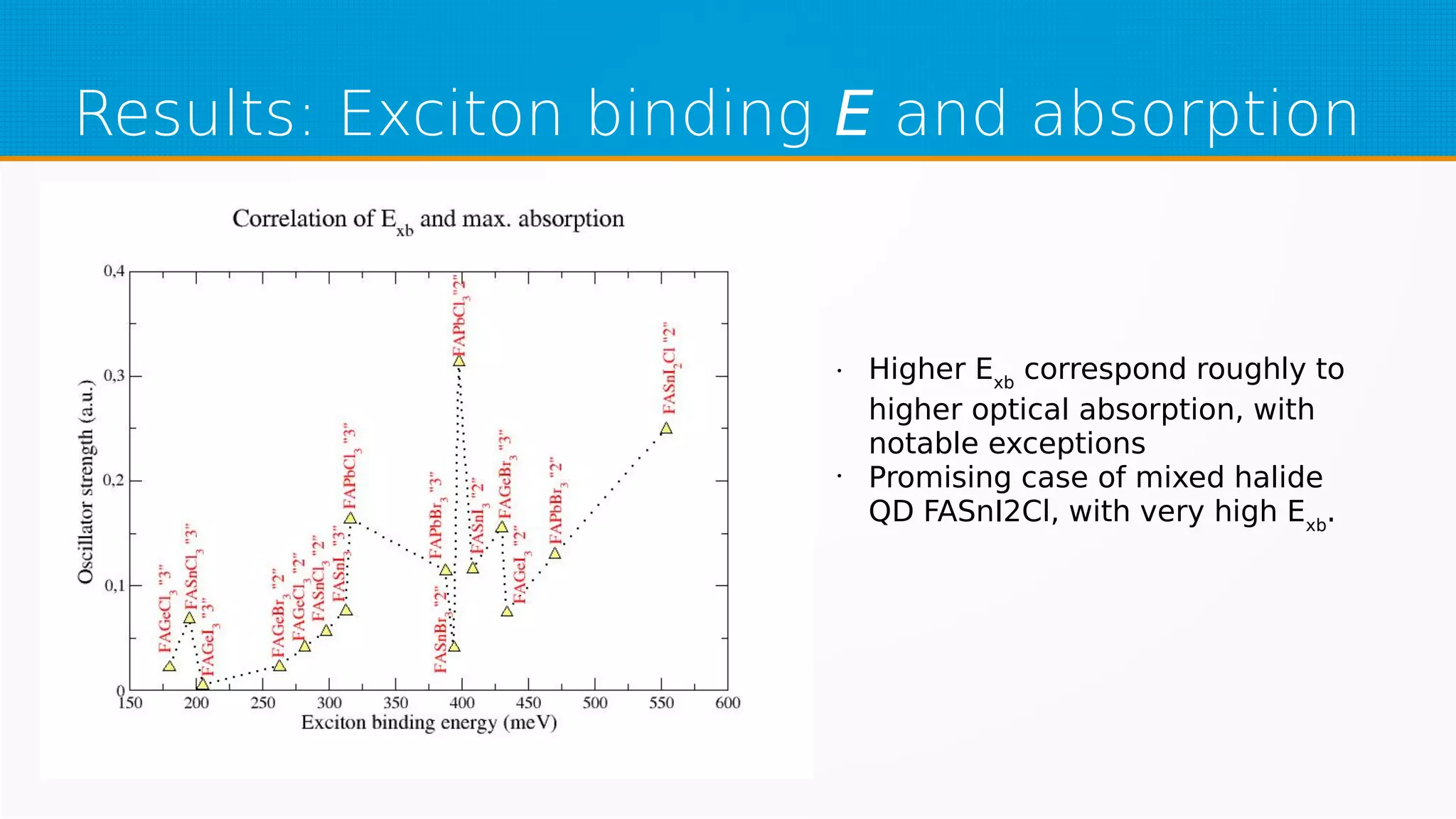
The study investigates hybrid halide perovskite quantum dots using DFT and TDDFT methods, focusing on structural and electronic properties. It reveals that gaps narrow with increasing sizes of quantum dots and heavier halogens, while exciton binding energies decrease with increased size. The results indicate a promising pathway for applications in optical absorption, particularly highlighting the performance of specific mixed halide quantum dots.

1. A DFT & TDDFT study of
Hybrid Halide Perovskite
Quantum Dots
Athanasios Koliogiorgos
Advanced Materials Group
Czech Technical University in Prague, Czech Republic

2. Previous research:
● ABX3
ultrasmall perovskites, where A
= Cs, MA (CH3
NH3
), B = Pb, Ge, Sn,
Ca, Sr and X = Cl, Br, I
●
Publication: A. Koliogiorgos et al, ACS
Omega 2018, 3, 12, 18917-24.

3. Previous research:
● ABX3
ultrasmall perovskites, where A
= Cs, MA (CH3
NH3
), B = Pb, Ge, Sn,
Ca, Sr and X = Cl, Br, I
●
Publication: A. Koliogiorgos et al, ACS
Omega 2018, 3, 12, 18917-24.
Continuation:
● FA (NH2
CNH2
) in place of MA (stable)
●
Larger sizes; convergence to
experimental QDs

4. Materials & initial structures
96 atoms
324 atoms
768 atoms
● FABX3
stoichiometry
●
B = Pb, Ge, Sn
●
X = Cl, Br, I

5. Computational approach
●
Problems:
– Big sizes (96 – 324 – 768 atoms; ~1 – 3 nm)
– Heavy atoms (I, Pb, …)
●
Limits of DFT computation ability
●
Combination of methods/functionals
●
Finite systems, real space

6. Computational approach
First optimization with tight binding (TB)
Fine tuning of geometry with GGA/DFT
Electronic ground states with hybrid DFT
Excited states with TDDFT

7. Computational approach
●
First optimization: tight-binding (TB), GFN-xTB code
GFN1-xTB
GFN2-xTB
•
S. Grimme, C. Bannwarth, P. Shushkov, J. Chem. Theor. Comput. 2017, 13(5), 1989-2009
•
C. Bannwarth, S. Ehlert, S. Grimme, J. Chem. Theory Comput. 2019, 15(3), 1652-1671

8. Computational approach
●
Final geometry optimization
●
PBE functional, def2-SVP
basis set, ORCA software
●
Accurate geometry, gross
underestimation of gaps

9. Computational approach
●
Electronic ground states
●
PBE0 functional
●
Def2/SVP + def/J basis sets
●
Accurate HOMO-LUMO gaps

10. Computational approach
●
Electronic ground states
●
PBE0 functional
●
Def2/SVP + def/J (auxiliary) basis sets
●
Accurate HOMO-LUMO gaps
●
Excited states
●
sTD-DFT: fast, large deviations
●
Tamm-Dancoff Approximation: very close/same to full TDDFT,
method of choice
●
Wavefunctions from ground state, geometry from PBE
●
Absorption spectra, optical gap, exciton binding energy

11. Results
●
Smooth convergence to bulk
band gap
●
Exciton binding energy
(=HOMO-LUMO gap – Optical
gap): decreasing accordingly
with increasing size
●
Respective bulk gaps
calculated with PAW method +
PBC + HSE06 hybrid functional
(VASP code)

12. Results
●
Density of states

13. Results: HOMO-LUMO/optical gaps
System H-L gap (eV) Opt.gap (eV) Exb
(meV)
FAPbCl3
“2” 4.742 4.344 398
FAPbCl3
“3” 4.315 3.999 316
FAPbCl3
“4” 4.003 - -
FAPbBr3
“2” 4.217 3.747 470
FAPbBr3
“3” 3.755 3.367 388
FASnI3
“2” 2.864 2.456 408
FASnI3
“3” 2.412 2.099 313
FASnBr3
“2” 3.467 3.073 394
FASnBr3
“3” 2.550 2.271 279
FASnCl3
“2” 3.667 3.369 298
FASnCl3
“3” 2.992 2.797 195
System H-L gap (eV) Opt.gap (eV) Exb
(meV)
FAGeI3
“2” 3.105 2.671 434
FAGeI3
“3” 1.998 1.793 205
FAGeBr3
“2” 2.584 2.321 263
FAGeBr3
“3” 2.399 1.969 430
FAGeCl3
“2” 4.491 4.209 282
FAGeCl3
“3” 3.218 3.038 180
FASnI2
Cl “2” 3.856 3.302 554
•
“2”, “3”, “4”: sizes of 2, 3, or 4 B cations
per dimension (96, 324, 768 atoms resp.)
•
HOMO-LUMO gap calc. with PBE0
•
Optical gap calc. with TDA-TDDFT

14. Results: HOMO-LUMO/optical gaps
● FAGeX3
, X = Cl, Br, I
●
Size: 3 Ge/dimension
●
HOMO-LUMO and optical gaps
narrow as we move from
lighter to heavier halogen
● Exb
does not decrease the
same way; indicator for
applications (FAGeBr3
)
● FAGeI3
gaps: below 2 eV

15. Results: Absorption spectra

16. Results: Exciton binding E and absorption
• Higher Exb
correspond roughly to
higher optical absorption, with
notable exceptions
•
Promising case of mixed halide
QD FASnI2Cl, with very high Exb
.

17. Conclusions
●
Narrowing of gaps with increasing size and convergence to
bulk
●
Narrowing of gaps from lighter to heavier halogen
● Decrease of Exb with increasing size – exceptions
●
Redshift of absorption for increasing size
●
No rule for increase of absorption strength with increasing size
→ focus on cases of increase
●
Next: focus on suitable gaps, dipole moments and absorption
➔
Study of FRET

18. www.nano.cvut.cz