1) The document provides step-by-step solutions to 3 problems involving complex roots and factoring polynomials. 2) For problem 1, the technique of sum of cubes is used to solve the equation 27x^3 + 1 = 0, yielding solutions of x = -1/3, x = [1 + i sqrt(3)] / 6, and x = [1 - i sqrt(3)] / 6. 3) Problems 2 and 3 similarly use techniques like sum of cubes, quadratic formula, and substitution to solve the equations x^3 + 8 = 0 and x^4 – 2x^2 – 8, providing the techniques and solutions.

1. Now We’ll Try!
As the class gets each step, we’ll
change the slide so make sure to
check if you’re on the right path!

2. Problem 1:
Solve 27x^3 + 1 = 0. Find all complex
roots. Name the technique, and give
the solutions.

3. • 27x^3 + 1 = (3x)^3 + (1)^3
• so use the sum of cubes
=(3x + 1) ((3x)^2 – 3x + 1^2)
= (3x + 1)(9x^2 – 3x + 1)

4. • Now set
3x + 1 = 0
and
9x^2 – 3x + 1 = 0

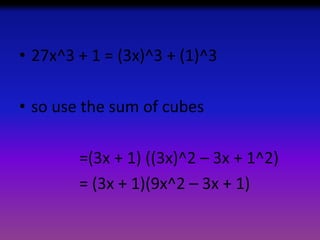
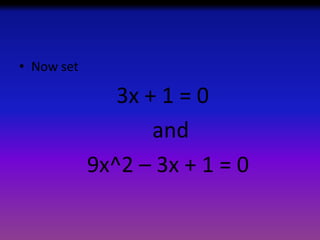
5. • So x = -1/3
x = [3 +/ sqrt(9 – 4(9)(1)] / 18
= [3 +/- sqrt(-27)] / 18
= [3 +/- 3i sqrt(3)] / 18
= [1 +/- i sqrt(3)] / 6
• Technique: sum of cubes, quadratic formula

6. Solutions:
x = -1/3
and
x = [1 + i sqrt(3)] / 6
and
x = [1 - i sqrt(3)] / 6

7. Problem 2:
• Solve: x^3 + 8 = 0
• Give the technique and the solutions!

8. • Technique: Sum of Cubes, Quadratic Formula
So
(x + 2)(x^2 + 2x + 4) = 0
x+2=0
and
x^2 + 2x + 4 = 0

9. x = -2
and
x = [2 +/- sqrt(4 – 4(1)(4))] / 2
x = [2 +/- sqrt(-12)] / 2
x = [2 +/- 2i sqrt(3)] / 2
x = 1 +/- i sqrt(3)
• Solutions: x = -2, x = 1 + i sqrt(3), and
x = 1 – i sqrt(3)

10. Problem 3:
•Factor x^4 – 2x^2 – 8

11. • Use a substitution technique to replace x^2
(x^2)^2 – 2(x^2) – 8
Let a = x^2
Then a^2 – 2a – 8 = (a – 4) (a + 2)

12. • Now that we’ve factored, we sub the “a” back
in
• So (x^2 – 4) (x^2 + 2) then we can continue
with difference of squares as normal
• = (x + 2) (x – 2) (x^2 + 2).
• So to note: our technique was to use
quadratic form!
• Now, we could solve these factors if we need
to find solutions!